. Um pouco sobre polígonos – Estrelas 1 – Clubes de Matemática da OBMEP

Um pouco sobre polígonos

Os applets disponibilizados nesta página poderão ser utilizados on-line e off-line
Para utilizá-los off-line, basta copiar os arquivos disponibilizados abaixo de cada applet e abri-los no GeoGebra do seu computador ou tablet.
Se você não tem o GeoGebra instalado, visite este site e procure pela versão adequada ao seu dispositivo.

Estrelas, uma apresentação informal

Que figuras podemos obter quando dividimos uma circunferência em n partes iguais e ligamos, consecutivamente, os n pontos que determinam essa divisão por segmentos de reta, saltando de k em k pontos?

I – Applets para ajudar no entendimento do problema proposto…

* Observando uma circunferência dividida em 7 partes iguais *

Disponibilizamos alguns applets e gifs, para você visualizar as figuras que obtemos a partir dos pontos que dividem uma circunferência em sete partes iguais.

Applet 1

Para utilizar o applet on-line, clique no botão Mostrar o Applet.
Para copiar o applet e utilizá-lo off-line, clique no botão Arquivo 1.

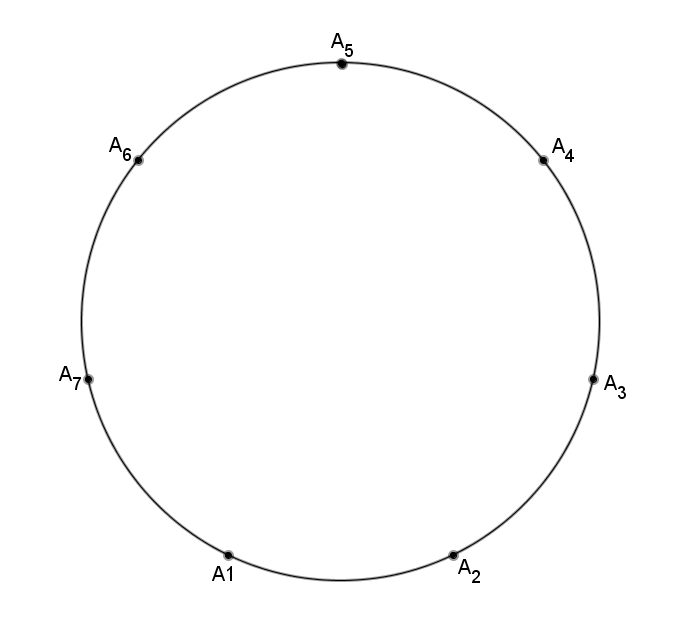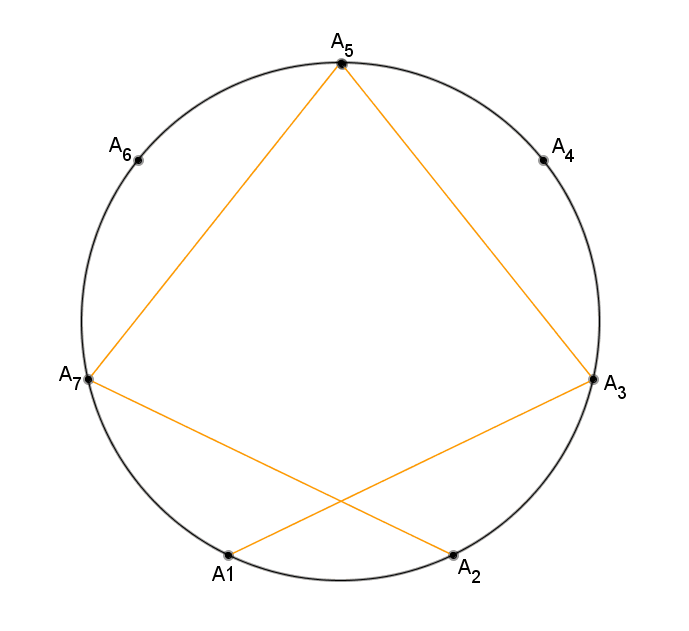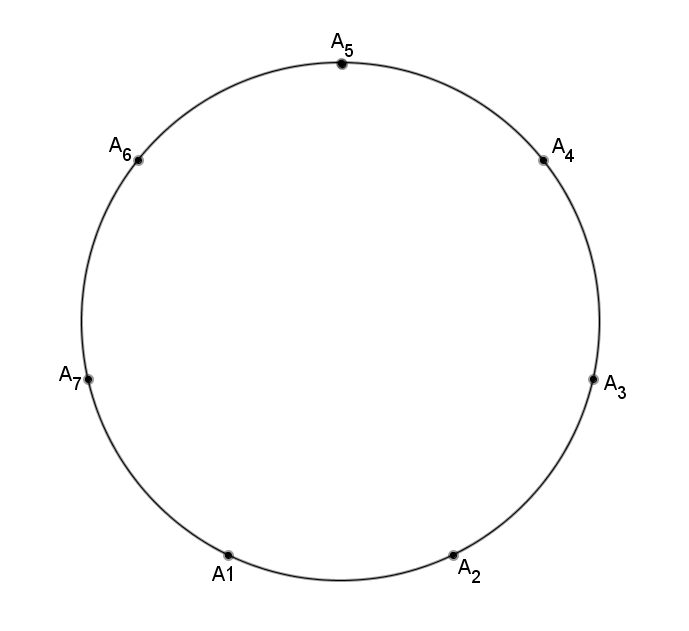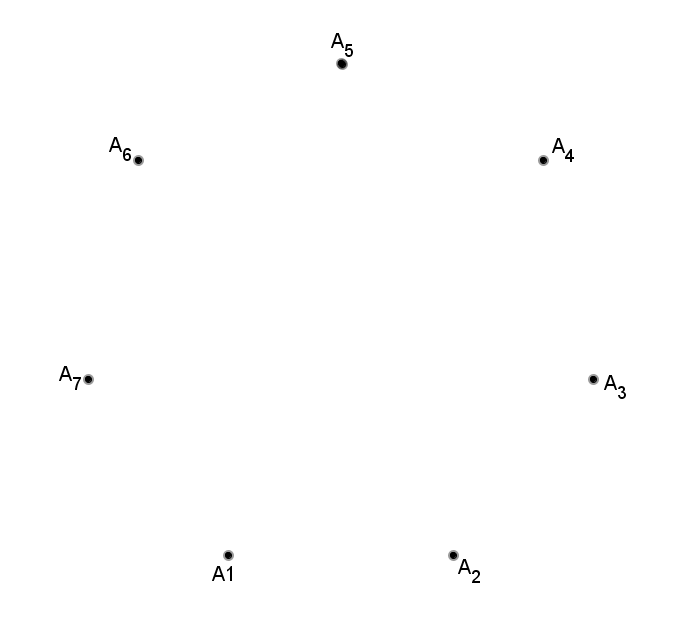
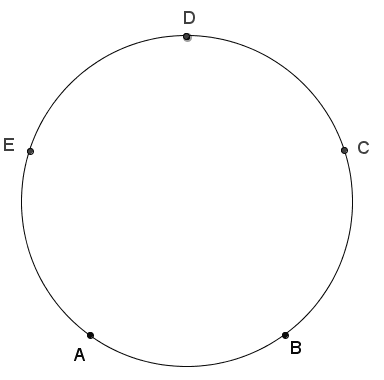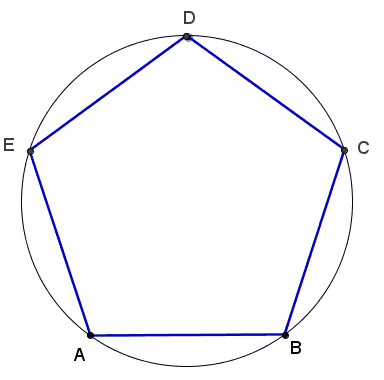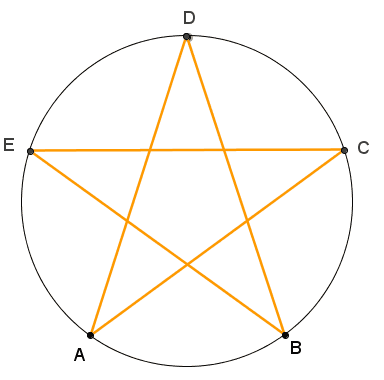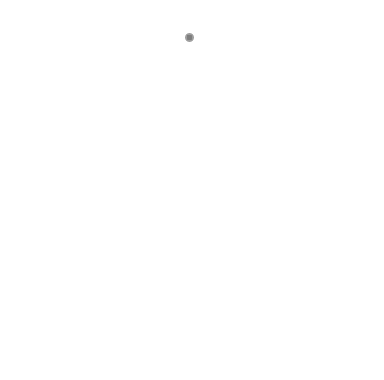
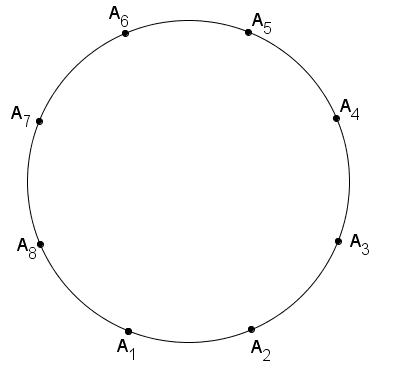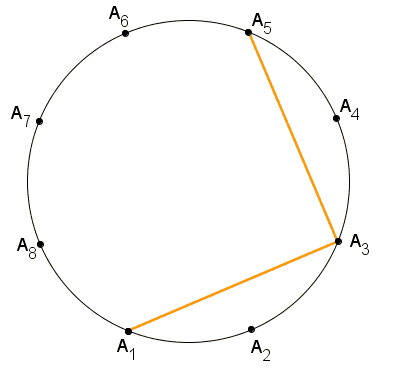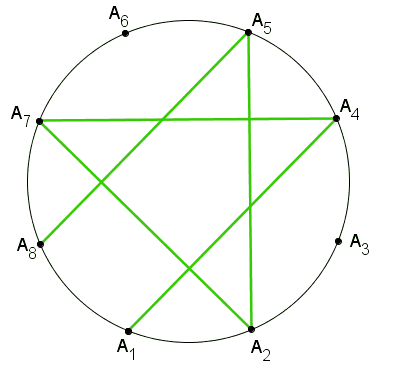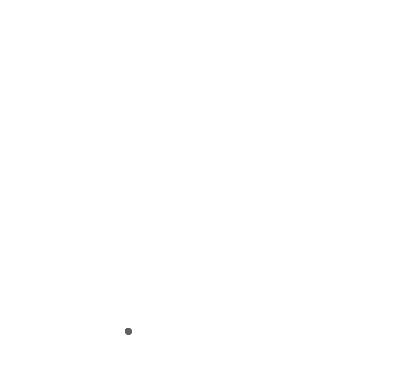
Você percebeu que, embora seja possível saltarmos de 1 em 1; de 2 em 2; de 3 em 3; de 4 em 4; de 5 em 5 e de 6 em 6 pontos, obtemos apenas três figuras diferentes?
Com o applet abaixo, você pode conferir as três figuras.

Applet 2

Para utilizar o applet on-line, clique no botão Mostrar o Applet.
Para copiar o applet e utilizá-lo off-line, clique no botão Arquivo 2.

Para uma visualização dinâmica das três figuras do applet 2,
utilize o gif animado abaixo.

Que tal repetir esse processo a partir de uma circunferência dividida em 5 partes iguais?
Para isso, utilize os applets abaixo…

* Observando uma circunferência dividida em 5 partes iguais *

Applet 3

Para utilizar o applet on-line, clique no botão Mostrar o Applet.
applet e utilizá-lo off-line, clique no botão Arquivo 3.

Com o applet anterior, é possível observar que podemos saltar de 1 em 1; de 2 em 2; de 3 em 3 e de 4 em 4 pontos, mas obtemos apenas duas figuras diferentes.
Com o próximo applet, você pode conferir as duas figuras…

Applet 4

Para utilizar o applet on-line, clique no botão Mostrar o Applet.
Para copiar o applet e utilizá-lo off-line, clique no botão Arquivo 4.

Para uma visualização dinâmica das duas figuras do applet 4,
utilize o gif animado abaixo.

Que figuras bonitas!
Mas será que, dividindo uma circunferência em um número qualquer de partes iguais e pulando do jeito que a gente quer, vamos sempre obter figuras como essas?

Essas figuras que chamaram a sua atenção são chamadas de estrelas. E pensando um pouquinho mais, talvez você mesmo consiga responder à sua pergunta.
Os próximos applets podem lhe ajudar com as respostas…

* Observando uma circunferência dividida em 8 partes iguais *

Applet 5

Para utilizar o applet on-line, clique no botão Mostrar o Applet.
Para copiar o applet e utilizá-lo off-line, clique no botão Arquivo 5.

Neste caso, ao pularmos de 4 em 4 pontos não aparecem figuras fechadas, pois obtemos vários segmentos de reta que concorrem em um mesmo ponto que não é extremidade de nenhum dos segmentos. Mas, aparentemente, ao saltarmos de 1 em 1; de 2 em 2; de 3 em 3; de 5 em 5, de 6 em 6 e de 7 em 7 pontos obtemos figuras fechadas que se repetem, como nas situações anteriores.
No próximo applet, registramos essas aparentes figuras fechadas.

Applet 6

Para utilizar o applet on-line, clique no botão Mostrar o Applet.
Para copiar o applet e utilizá-lo off-line, clique no botão Arquivo 6.

Para uma visualização dinâmica das três figuras do applet 6, utilize o gif animado abaixo.
Observe mais uma vez a figura resultante ao pularmos de 2 em 2 pontas

Pulos que não definem figuras fechadas?
Estrelas falsas?
Complicou…

Calma, não é tão complicado quanto parece…
Vamos observar o que acontece quando dividimos uma circunferência em 9 partes iguais (arcos congruentes), para depois fazermos algumas observações. Neste caso também teremos estrelas falsas…

* Observando uma circunferência dividida em 9 partes iguais *

Applet 7

Para utilizar o applet on-line, clique no botão Mostrar o Applet.
Para copiar o applet e utilizá-lo off-line, clique no botão Arquivo 7.

Aqui, podemos saltar de 1 em 1; de 2 em 2; de 3 em 3; de 4 em 4; de 5 em 5, de 6 em 6, de 7 em 7 e de 8 em 8 pontos: em todos os casos obteremos figuras aparentemente fechadas que podem se repetir.
No próximo applet, registramos as figuras.

Applet 8

Para utilizar o applet on-line, clique no botão Mostrar o Applet.
Para copiar o applet e utilizá-lo off-line, clique no botão Arquivo 8.

Esse último caso me mostrou que o aparecimento das chamadas estrelas falsas (ainda não entendi bem o que é isso…) não decorre de dividirmos a circunferência em um número par de arcos iguais.
Apareceram estrelas falsas quando dividimos a circunferência em 8 partes iguais, mas também quando dividimos a circunferência em 9 partes.

Isso mesmo!
Vamos, então, registrar algumas observações sobre os quatro casos apresentados,
circunferências divididas em 5, 7, 8 e 9 partes iguais,
para tentarmos responder à pergunta inicial proposta.

II – Respondendo ao problema proposto

Problema
Se [tex]A_1,\, A_2,\, \cdots , A_n [/tex] são pontos que dividem uma dada circunferência em [tex]n[/tex] partes iguais, que figuras podemos obter se ligarmos por segmentos de reta esses [tex]n[/tex] pontos, consecutivamente, de [tex]k[/tex] em [tex]k[/tex] pontos?

Na nossa discussão, [tex]n[/tex] representará o número de partes iguais (arcos congruentes) em que uma dada circunferência foi dividida, enquanto [tex]k[/tex] corresponderá ao número de saltos feitos para traçarmos segmentos de reta ligando pontos dessa divisão.
Vamos, inicialmente, reunir na tabela abaixo algumas das informações que podemos obter com os applets que foram aqui disponibilizados.

[tex]n[/tex]	[tex]k[/tex]	figura obtida
5	1	pentágono regular
	2	estrela de cinco pontas (pentagrama)
	3	estrela de cinco pontas (pentagrama)
	4	pentágono regular
7	1	heptágono regular
	2	estrela de sete pontas 1
	3	estrela de sete pontas 2
	4	estrela de sete pontas 2
	5	estrela de sete pontas 1
	6	heptágono regular
8	1	octógono regular
	2	estrela de oito pontas falsa
	3	estrela de oito pontas 1
	4	segmentos de reta concorrentes
	5	estrela de oito pontas 1
	6	estrela de oito pontas falsa
	7	octógono regular
9	1	heptágono regular
	2	estrela de nove pontas 1
	3	estrela de nove pontas falsa
	4	estrela de nove pontas 2
	5	estrela de nove pontas 2
	6	estrela de nove pontas falsa
	7	estrela de nove pontas 1
	8	heptágono regular

Como eu não entendi o que são estrelas falsas, eu responderia à pergunta do problema dizendo que, quando é formada uma figura fechada, essa figura é um polígono regular (quando damos os maiores ou os menores pulos) ou uma estrela. Mas podem aparecer segmentos de reta…

Muito boa a sua observação com relação ao aparecimento de polígonos regulares!
Com relação às estrelas falsas, o problema é o que chamamos de figura fechada, na Matemática…
Observe atentamente as duas situações apresentadas nas quais apareceram estrelas falsas: oito e nove pontas.

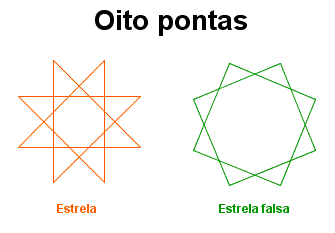
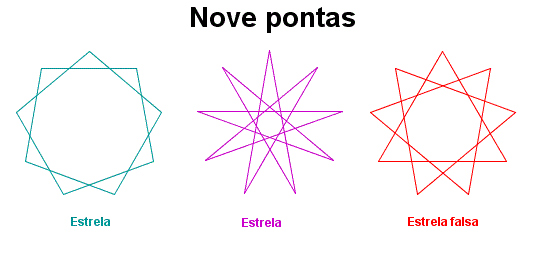
Em cada “estrela”, caminhe sobre seus lados, a partir de uma de suas pontas.
O que aconteceu?

Nas chamadas estrelas, partimos de uma de suas pontas e, sem tirar o lápis do papel onde a figura está desenhada, passamos por todos os seus lados e chegamos na ponta da qual partimos. Nas estrelas falsas, para voltarmos para a ponta inicial passando por todos os seus lados, temos que tirar o lápis do papel pelo menos uma vez…
É isso?

Muito bem, você está corretíssimo!
Na verdade, as estrelas falsas não são o que classificamos na matemática como figuras fechadas; elas são sobreposições de polígonos regulares.
Observe.

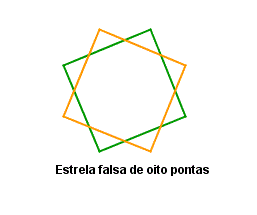A estrela falsa de oito pontas é a sobreposição de dois quadrados,
logo não consideramos uma figura fechada, propriamente dita.
9_1

A estrela falsa de nove pontas é a sobreposição de três triângulos equiláteros,
portanto também não é considerada uma figura fechada.

Agora sim…
O que está sendo chamado de estrela, digamos verdadeira, é aquela na qual partimos de uma de suas pontas e, percorrendo continuamente um único caminho, passamos por todas as outras pontas e voltamos para a ponta da qual partimos.

Correto, parabéns!
Vamos ver mais um exemplo de estrela falsa: ela aparece quando dividimos uma circunferência em 6 partes iguais e tem, portanto, 6 pontas.

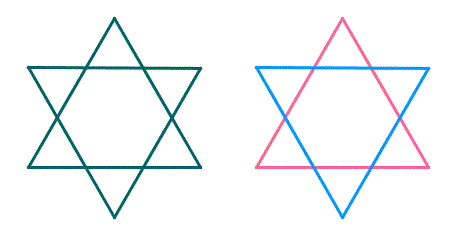Aqui temos a sobreposição de dois triângulos equiláteros.
Portanto, temos dois caminhos e, consequentemente, uma figura não fechada.

Bom, agora eu consigo responder à pergunta proposta:
Quando unimos por segmentos de retas os pontos que dividem uma circunferência em [tex]n[/tex] partes iguais, pulando de [tex]k[/tex] em [tex]k[/tex] pontos, podemos obter segmentos de retas concorrentes, polígonos regulares, estrelas e falsas estrelas.

Vamos, então, registrar, mais uma vez, a pergunta do problema, mas agora acompanhada de uma resposta.

Problema:

Se [tex]A_1,\, A_2,\, \cdots , A_n [/tex] são pontos que dividem uma dada circunferência em [tex]n[/tex] partes iguais, que figuras podemos obter se ligarmos por segmentos de reta esses [tex]n[/tex] pontos, consecutivamente, de [tex]k[/tex] em [tex]k[/tex] pontos?

Resposta:

O problema só tem sentido se [tex]n[/tex] for um número natural tal que [tex] n ≥ 2[/tex]>.

Se [tex] n= 2[/tex], a figura obtida é, necessariamente, um segmento de reta.
Se [tex] n= 3[/tex] a figura obtida é, necessariamente, um triângulo equilátero.
Se [tex] n > 3[/tex], podem ser obtidas as seguintes figuras:

polígonos regulares;
segmentos de reta concorrentes;
estrelas;
estrelas falsas (sobreposição de polígonos).

III – Explorando o problema proposto

Se formos dividir uma circunferência em n partes iguais, podemos prever de quantos em quantos pontos devemos pular para obtermos estrelas (não falsas) com n pontas, mesmo antes de fazermos a divisão?

Nossa!!!!!!
Será que isso é possível ?!?!