Um pouco sobre polígonos
Estrelas, uma definição algorítmica*
 |
Vamos formalizar um pouco do que foi discutido na sala sobre Estrelas. |
I – Figuras (n , k)
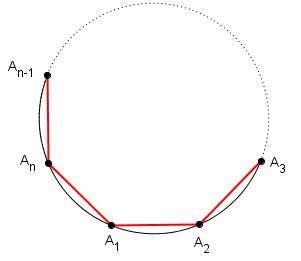
Chamamos de figura (n , k) a figura geométrica definida pela união dos segmentos de reta obtidos mediante os seguintes passos:
▸ PASSO 1 – Divide-se uma circunferência em [tex] n [/tex] partes iguais ([tex] n [/tex] arcos congruentes). Os pontos da divisão serão denominados “nós”.
▸ PASSO 2 – Escolhe-se um dos nós. Denomina-se esse nó de “ponto visitado”.
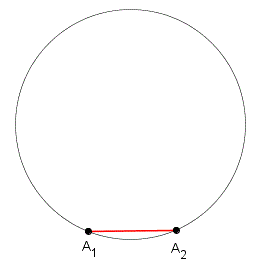
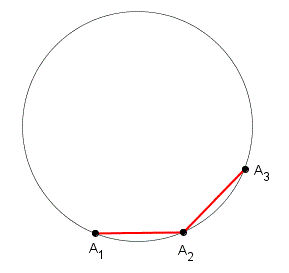
▸ PASSO 3 – Traça-se um segmento de reta do último ponto visitado até o nó que se obtém saltando-se [tex] k [/tex] arcos consecutivos, no sentido anti-horário, a partir desse último ponto visitado. Esse nó de chegada será também denominado “ponto visitado“.
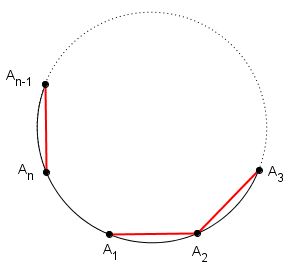
▸ PASSO 4 – Repete-se o PASSO 3 até que o segmento traçado termine em um ponto já visitado.
Que objetos geométricos podemos classificar
como figuras (n , k) ?
As figuras (n , k) são obtidas quando atribuímos para as variáveis [tex] n [/tex] e [tex] k [/tex] valores numéricos estabelecidos na definição, ou seja, números naturais tais que 0 < k < n . Observem que, dividida uma circunferência em n arcos congruentes, os segmentos de reta que definem uma figura (n , k) são cordas da circunferência fixada, todas com o mesmo comprimento e tendo como extremidades pontos que dividiram a circunferência nas [tex] n [/tex] partes iguais. O comprimento constante dessas cordas depende do número [tex] k [/tex], já que este determina a quantidade de arcos que serão pulados na definição de cada segmento.
Vejamos alguns exemplos dessas figuras.
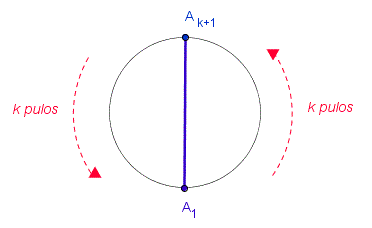
➥Se [tex] k [/tex] for um número natural não nulo e n = 2k, então a figura (n , k) definida será um segmento de reta.
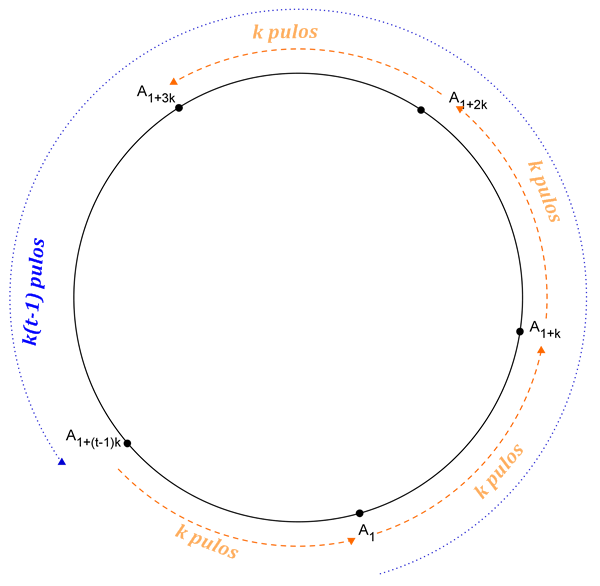
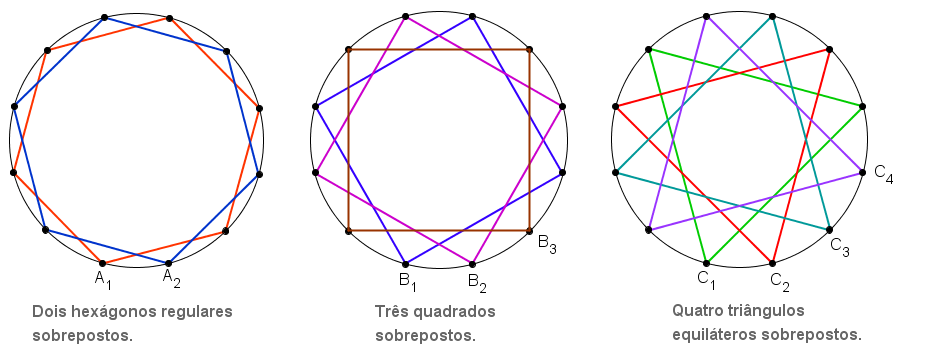
☞ Vale observar que, fixado um número natural não nulo [tex] k [/tex], se repetirmos o processo de construção da figura (2k , k) por [tex] k [/tex] vezes, tomando, nos respectivos PASSO 2, sucessivamente, os pontos [tex]A_1, \, A_2, \, \cdots , A_k [/tex], obteremos aqueles segmentos de reta concorrentes que observamos na Sala 1 sobre Estrelas.
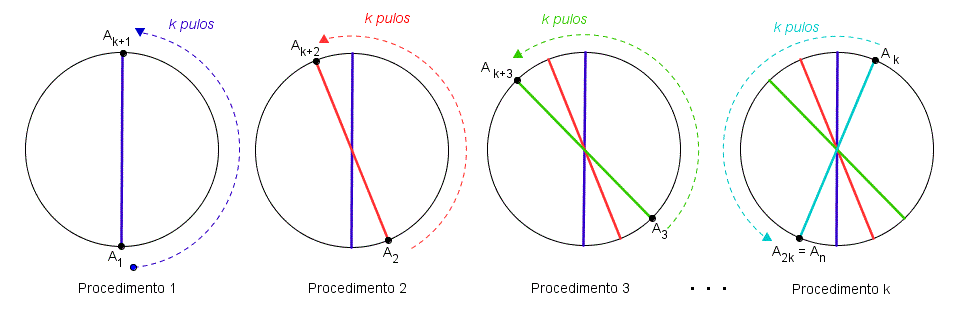
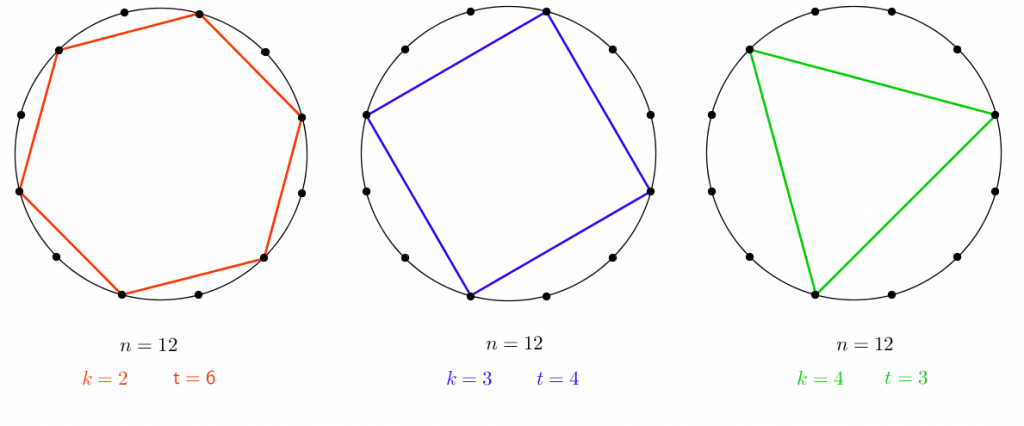
➥ Se [tex] n [/tex] for um número natural tal que n > 2 e k = 1, a figura (n , k) será um polígono regular de [tex] n [/tex] lados.
➥ Seja [tex] n [/tex] um número natural maior do que 5.
Se [tex] k [/tex] é um número natural tal que [tex] k [/tex] seja um divisor de [tex] n [/tex] e 1 < k < [tex]\dfrac{n}{2}[/tex], então a figura (n , k) será um polígono regular com menos de [tex] n [/tex] lados (mais especificamente, com [tex]\dfrac{n}{k}[/tex] lados).
☞ Vale, também, observar que, fixado um número natural não nulo [tex] k [/tex] que seja um divisor de [tex] n [/tex], se repetirmos o processo de construção da figura (n , k) por [tex] k [/tex] vezes, tomando, nos respectivos PASSO 2, sucessivamente, os pontos A1 , A2 , … , Ak, obteremos [tex] k [/tex] polígonos regulares com [tex]\dfrac{n}{k}[/tex] lados, ou seja, aquelas figuras que denominamos Falsas Estrelas, na Sala 1 sobre Estrelas.
➥ Sejam [tex] n [/tex] e [tex] k [/tex] números naturais tais que 0 < k < n .
Então as figuras (n , k) e (n , n − k) construídas a partir de uma mesma circunferência são iguais.
Esse último exemplo, na verdade, é uma importante propriedade das figuras (n , k): fixado um número natural [tex] n [/tex], com 2 < n, para conhecer todas as figuras (n , k), basta analisar os casos em que [tex] k [/tex] é um número natural não nulo tal que k < [tex]\dfrac{n}{2}[/tex] . Afinal, já sabemos o que acontece quando [tex] k =\dfrac{n}{2}[/tex], não é?
 |
Agora, vamos utilizar as figuras (n , k) para tentar responder à pergunta formulada no final da discussão da primeira Sala sobre Estrelas. |
II – Analisando as situações apresentadas
Iniciamos a discussão da Sala 1 sobre Estrelas formulando um problema, que foi respondido. Em seguida, aprofundamos a discussão e formulamos uma nova pergunta, que ficou sem resposta. Vamos retomar o problema inicial, para tentar respondê-lo utilizando a ideia de figuras (n , k), e depois completar a discussão respondendo a segunda pergunta. Para tanto, sejam [tex] n [/tex] e [tex] k [/tex] números naturais tais que 0 < k < n .
Que figuras podemos obter ao dividirmos uma circunferência em [tex] n [/tex] partes iguais e ligarmos, consecutivamente, os [tex] n [/tex] pontos que determinam essa divisão por segmentos de reta, saltando de [tex] k [/tex] em [tex] k [/tex] pontos ?
Sejam A1 , A2 , … , An os pontos que dividem uma dada circunferência em [tex] n [/tex] partes iguais. As figuras que obtemos ao ligarmos, consecutivamente, os [tex] n [/tex] pontos que determinam a divisão por segmentos de reta, saltando de [tex] k [/tex] em [tex] k [/tex] pontos (saltando [tex] k [/tex] arcos) são figuras (n , k) (apenas uma ou mais figuras) e os pontos A1 , A2 , … , An são os seus respectivos nós. Logo, a pergunta sem resposta da Sala anterior pode ser assim reformulada:
Sejam [tex] n [/tex] e [tex] k [/tex] números naturais tais que 0 < k < n . Podemos concluir se uma figura (n , k) é uma estrela não falsa com [tex] n [/tex] pontas, a partir, apenas, dos valores numéricos de [tex] n [/tex] e [tex] k [/tex]?
Vamos em busca de respostas.
Observamos, inicialmente que, como 0 < k < n , necessariamente, n ≥ 2. Mas o que mais podemos concluir, a partir das discussões já feitas nesta Sala e, também, na Sala 1 sobre Estrelas?
Vejamos:
- Se n for par e [tex]k=\dfrac{n}{2}[/tex], obteremos um segmento de reta.
- Antes de prosseguirmos com nossa análise, lembramos que as figuras (n , k) e (n , n − k) são iguais, para cada número k fixado.
➨ Portanto, podemos considerar na nossa discussão apenas os números naturais k tais que [tex]k\lt\dfrac{n}{2}[/tex]; pois, se a figura (n , k) for uma estrela de [tex] n [/tex] pontas, então a figura (n , n – k) também o será.
- Fixado n, a figura (n , 1) é um polígono regular de [tex] n [/tex] lados.
- Fixado n, se k é um divisor de n e k ≠ 1, então a figura (n , k) é um polígono regular com menos de [tex] n [/tex] lados.
(Aqui, particularmente é possível a repetição contínua do processo de construção de figuras (n , k) e, neste caso, obteremos [tex] k [/tex] polígonos regulares com [tex]\dfrac{n}{k}[/tex] lados – estrelas falsas.)
Particularmente, se n = 2, então k = 1 e a figura (n , k), ou seja, a figura (2 , 1) é um segmento de reta.
(Se n > 2, é possível a repetição contínua do processo da construção de figuras (n , 1) e, neste caso, obteremos n/2 segmentos de reta concorrentes.)
➨ Dessa forma, não encontraremos estrelas quando [tex]k=\dfrac{n}{2}[/tex].
➨ Logo, não encontraremos estrelas para k = 1.
➨ Portanto, não encontraremos estrelas quando k for um divisor de [tex] n \, . [/tex]
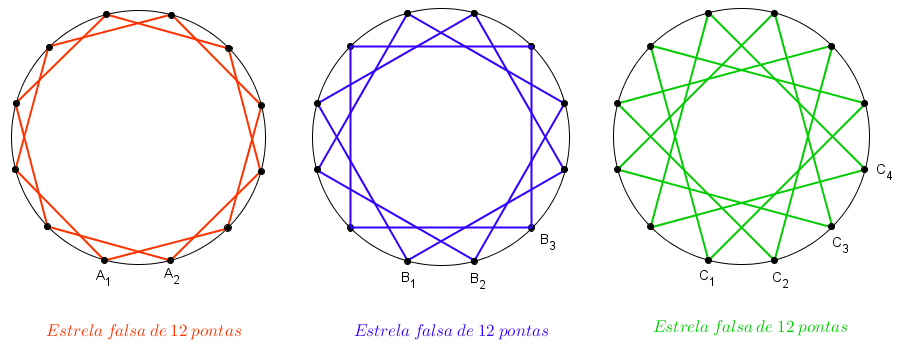
Já observamos algumas situações nas quais não obtemos estrelas. Com isso, nesse ponto da discussão, alguém pode conjecturar que, se [tex] k [/tex] não for um divisor de [tex] n [/tex], então a figura (n , k) será uma estrela de [tex] n [/tex] pontas. Será que essa afirmação é correta?
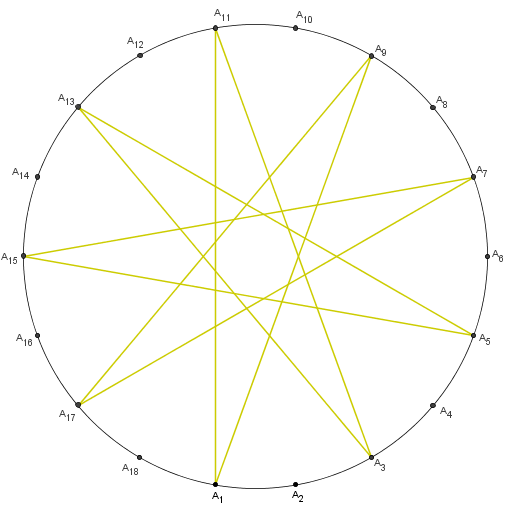
Observe a figura (15 , 6).
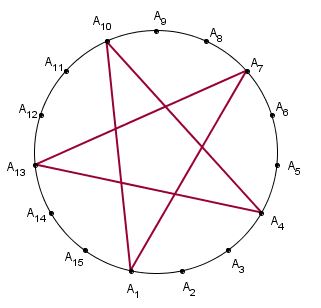
A figura (15 , 6) é, de fato, uma estrela, mas é uma estrela de cinco pontas, ou seja, não visitamos os 15 nós obtidos na divisão da circunferência. E note que essa estrela pode ser feita com menos de 15 nós, não é?
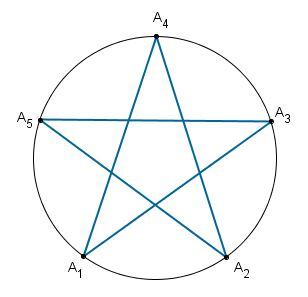
☞ Aqui, vale a pena observarmos que se repetirmos o processo de construção da figura (15 , 6) 3 vezes, tomando em cada PASSO 2, sucessivamente, os pontos A1 , A2 , A3, visitaremos os 15 pontos e obteremos uma bela figura. Mas o resultado final não é o que definimos como uma Estrela e sim a sobreposição de três estrelas de cinco pontas.
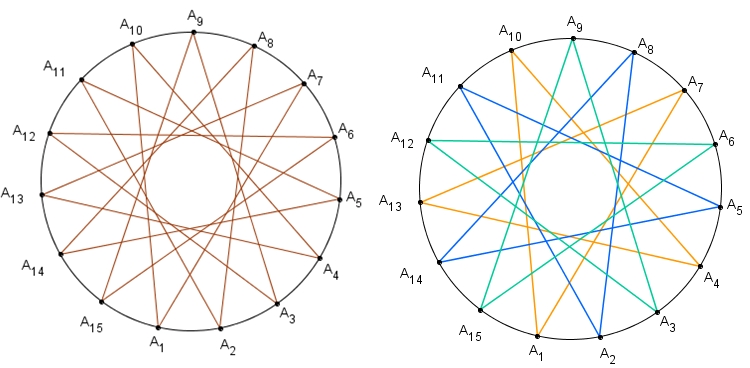
➨ Pelo exposto, podemos encontrar estrelas nas situações nas quais k não é divisor de [tex] n [/tex], mas não encontraremos necessariamente estrelas de [tex] n [/tex] pontas.
Pelo até agora discutido, não ficamos com muitas possibilidades para caracterizarmos uma estrela de n pontas como um caso particular das figuras (n , k), para [tex] n [/tex] fixo:
- se k é um divisor de n não definimos estrelas;
- se [tex] k [/tex]e n têm fatores distintos de 1 em comum, podemos até definir estrelas, mas não necessariamente estrelas com n pontas.
Se k for distinto de 1, sobrou, então, para as estrelas de n pontas a condição de que k e n não tenham fatores em comum diferentes de 1 . Ao que tudo indica, a resposta para a pergunta não respondida é:
Uma figura (n , k) será uma estrela de n pontas, se 1 < k < n − 1 e o máximo divisor comum entre n e k for 1 ([tex] mdc(n,k) = 1 [/tex]).
No entanto, precisamos mais do que falta de opções para garantirmos a veracidade dessa nossa conjectura; mas vamos deixar essa discussão para a próxima sessão.
 |
Você sabe calcular o MDC de dois números naturais? |
III – Afinal, uma definição para as nossas estrelas
Vamos iniciar a nossa discussão observando que, mesmo que [tex] n [/tex] e [tex] k [/tex] sejam números naturais tais que n > 4 e 1 < k < n − 1 , o que temos até agora não nos garante que:
(1) Os quatro passos da definição de figuras (n , k) resultam em um conjunto finito de segmentos de reta.
(2) Se [tex] mdc(n,k) = 1 [/tex], então a figura (n , k) é uma estrela de [tex]n[/tex] pontas.
(3) Se uma figura (n , k) for uma estrela de [tex]n[/tex] pontas, então [tex] mdc(n,k) = 1 [/tex].
E a veracidade dessas três afirmações são essenciais para sustentar a resposta que conjecturamos para a intrigante pergunta formulada na Sala 1.
A primeira observação está intimamente ligada ao * colocado no título desta Sala: Estrelas, uma definição algorítmica*. Para esclarecer o * e a observação (1), lembremos o que é um algoritmo.
Sem muito formalismo, podemos dizer que um algoritmo é uma sequência finita de instruções (passos) que permitem a execução de uma dada tarefa.
Por ser uma sequência finita de instruções, é essencial que a execução das regras que definem um algoritmo termine em um determinado momento.
Embora a definição de figuras (n , k) tenha sido feita a partir de uma sequência de, apenas, quatro passos, o terceiro passo pode ser executado mais de uma vez; portanto, o que nos garante que o processo de definição de uma figura (n , k) sempre terá um fim, já que [tex]n[/tex] poderá ser, inclusive, um número natural muito grande?
A condição de parada do nosso algoritmo de definição é traçar um segmento de reta cuja extremidade final seja um ponto (nó) já visitado; assim cabe a pergunta: esse ponto existe para qualquer número natural [tex]n[/tex] maior do que [tex]1[/tex]?
A resposta positiva para essa pergunta encontra justificativa em uma ferramenta utilizada frequentemente na matemática: Princípio da Casa dos Pombos. No nosso caso, esse princípio garante matematicamente um fato que intuitivamente é fácil de ser observado: com efeito, como a circunferência que define a figura (n , k) foi dividida em [tex] n [/tex] arcos congruentes, então existem [tex] n [/tex] nós e, portanto, existirão, no máximo, [tex] n [/tex] pontos visitados. Dessa forma, independentemente do número natural [tex] n [/tex], o passo 3 da definição poderá ser repetido, no máximo, [tex] n [/tex] vezes.
Assim, temos garantidas duas condições:
➨ A definição de figuras (n , k) é, de fato, um algoritmo.
➨ A definição de figuras (n , k) aplicada particularmente para números naturais [tex] n [/tex] e [tex] k [/tex] tais que mdc(n,k) = 1 resulta, certamente, em um conjunto finito de segmentos de reta.
Embora verdadeiras, justificar matematicamente as afirmações (2) e (3) é um pouco complicado. Podemos fazê-lo utilizando propriedades do estudo dos restos de uma divisão euclidiana ou utilizando números complexos, mais especificamente, raízes primitivas da unidade. De qualquer forma, a justificativa matemática das duas afirmações foge dos objetivos desta Sala de Estudo; mas se você se interessou pelos dois caminhos indicados para a demonstração das afirmações, consulte este texto: Polígonos Estrelados Regulares.
Considerando a veracidade das afirmações (1), (2) e (3), faz sentido definirmos, finalmente, as nossas estrelas:
Sejam [tex] n [/tex] e [tex] k [/tex] números naturais tais que n > 4 e 1 < k < n − 1 . Chamamos de estrela de [tex] n [/tex] pontas a toda figura (n , k) tal que [tex] n [/tex] e [tex] k [/tex] sejam primos entre si, ou seja, [tex] mdc(n,k) = 1 [/tex].
 |
Um objeto geométrico definido algebricamente! |
IV – Novos exemplos e novas considerações
Agora ficou muito fácil determinar os valores de [tex] k [/tex] que definem estrelas de [tex] n [/tex] pontas em uma circunferência dividida em [tex] n [/tex] partes iguais: para cada natural [tex] k [/tex], com 0 < k < n, basta verificar se [tex] mdc(n,k) = 1 [/tex], ou seja, se [tex] n [/tex] e [tex] k [/tex] são o que a matemática define como primos entre si. Vejamos alguns exemplos.
➥Se [tex]n=20[/tex], as estrelas de 20 pontas aparecem quando k = 3; 7; 9; 11; 13; 17.
Além disso, são iguais as estrelas definidas para saltos de “3 em 3 e 17 em 17”; “7 em 7 e 13 em 13” e “9 em 9 e 11 em 11”.
Quando [tex]k=1[/tex] ou [tex]k=19[/tex], definimos um icoságono regular.
OBMEP_srdg, criado com o GeoGebra
Você também pode utilizar o gif animado para visualizar o icoságono regular e as três estrelas.
Você pode, ainda, copiar o arquivo abaixo e utilizá-lo em seu computador.
Pelo exposto no início da discussão, quando k = 2; 4; 5 obtemos polígonos regulares de, respectivamente, 10, 5 e 4 lados.
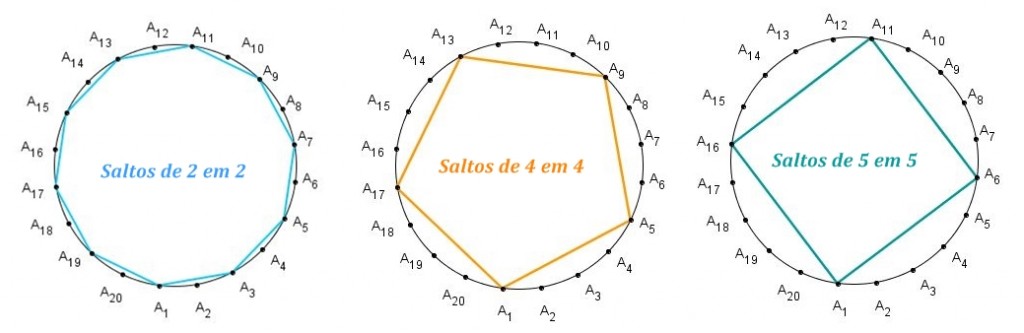
Como as figuras (n , k) e (n , n − k) são as mesmas, quando k = 18; 16; 15 obtemos, também, polígonos regulares de, respectivamente, 10, 5 e 4 lados.
➥Se [tex]n=13[/tex], só não temos estrelas de 13 pontas para [tex]k=1[/tex] e [tex]k=12[/tex], quando obtemos um tridecágono regular.
OBMEP_srdg, criado com o GeoGebra
Se for conveniente, copie o arquivo abaixo e utilize-o em seu computador.
|
Nos exemplos acima, para [tex]n=13[/tex] foi possível classificar todos os saltos, antes de executá-los, mas para [tex]n=20[/tex]; faltou determinar o que acontece quando saltamos de 6 em 6 (ou de 14 em 14) e de 8 em 8 (ou de 12 em 12). Para esses casos também conseguimos, de alguma forma, prever o que vai acontecer? |
 |
 |
Sim! |
Ao dividirmos uma circunferência em [tex] n [/tex] partes iguais e ligarmos, consecutivamente, os [tex] n [/tex] pontos que determinam a divisão por segmentos de reta, saltando de [tex] k [/tex] em [tex] k [/tex] pontos obtemos o que definimos como figuras (n , k).
Mas, fixado [tex] n \gt 1[/tex], que figuras (n , k) obtemos para cada inteiro [tex] k [/tex] tal que 0 < k < n ?
Pelo que já discutimos nesta Sala, resta, apenas, observar o que acontece para inteiros [tex] k [/tex] tais que “mdc(n,k) ≠ 1 e [tex] k [/tex] não é divisor de [tex] n [/tex]”.
Encontramos resposta para esse caso na Teoria dos Números, mais uma vez! Existe uma propriedade muito útil dos números naturais que nos garante que:
- Se a, b e d são números naturais não nulos, então mdc(a · d , b · d) = d · mdc(a , b) .
Pois bem, no nosso caso é possível mostrar (não faremos, pois também foge dos objetivos desta Sala de Estudos) que:
- Se d = mdc(n , k) , n = a · d e k = b · d , então a figura (n , k) é a figura (a , b).
Mais ainda, como [tex]a=\dfrac{n}{d}[/tex], [tex]b=\dfrac{k}{d}[/tex] e [tex]d=mdc(n, k)[/tex], uma segunda propriedade dos números inteiros nos garante que mdc(a , b) = 1 e, dessa forma, a figura (a , b) é uma estrela de a pontas.
|
Se eu entendi a observação, como n = 20 = 10 · 2 e k = 6 = 3 · 2 , a figura (20 , 6) é uma estrela de 10 pontas. |
 |
 |
Isso mesmo! |
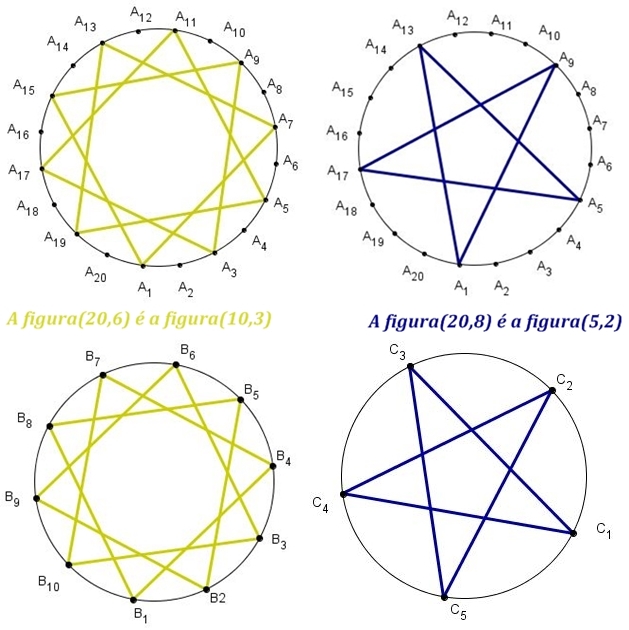
 |
Vamos passar a limpo as nossas ideias… |
V – Um roteiro
Com tudo que desenvolvemos e assumimos nesta Sala, podemos estabelecer um roteiro para responder a pergunta geral formulada. Vejamos…
Fixado um número natural não nulo [tex] n [/tex], que figuras (n , k) obtemos para cada inteiro [tex] k [/tex] tal que 0 < k < n ?
Sejam [tex] n [/tex] e [tex] k [/tex] números naturais tais que 0 < k < n.
⇝ Passo 1: Verifique se k ≤ [tex]\dfrac{n}{2}[/tex].
- Se k ≤ [tex]\dfrac{n}{2}[/tex] , faça t = k e aplique os passos seguintes para t .
- Se k ≥ [tex]\dfrac{n}{2}[/tex], faça t = n – k e aplique os passos seguintes para t .
Com esse passo asseguramos que trabalharemos apenas com números naturais não nulos, no máximo, iguais a [tex]\dfrac{n}{2}[/tex] e sem perder a generalidade do problema, uma vez que a figura (n , k) e a figura (n , n – k) são iguais.
⇝ Passo 2: Verifique se t = [tex]\dfrac{n}{2}[/tex] .
- Se t = [tex]\dfrac{n}{2}[/tex] , então [tex] n [/tex] é par e a figura (n , t) é um segmento de reta.
- Se t ≠ [tex]\dfrac{n}{2}[/tex] , vá para o Passo 3.
Se o próximo Passo for executado, significa que t ≠ [tex]\dfrac{n}{2}[/tex] ; portanto, nos próximos passos, t < [tex]\dfrac{n}{2}[/tex] e n > 2 , necessariamente.
⇝ Passo 3: Verifique se t = 1 .
- Como n > 2 , se t = 1 , então a figura (n , t) é um polígono regular de n lados.
- Se t ≠ 1 , vá para o Passo 4.
Antes de executarmos o Passo 4, precisamos calcular o mdc(n , t).
⇝ Passo 4: Seja d = mdc(n , t).
- Se d = 1, como t ≠ 1 , então a figura (n , t) é uma estrela de n pontas.
- Se d ≠ 1, vá para o Passo 5.
Importante: Se o próximo passo for executado, então d = mdc(n , t) ≠ 1, assim [tex]\dfrac{n}{d} \lt n \, [/tex] e [tex] \, \dfrac{n}{t} \lt n[/tex].
⇝ Passo 5: Verifique se t é um divisor de [tex] n [/tex].
- Se t for um divisor de [tex] n [/tex], a figura (n , t) é um polígono regular de [tex]\dfrac{n}{t}[/tex] lados.
- Se t não for um divisor de [tex] n [/tex], então a figura (n , t) é uma estrela de [tex]\dfrac{n}{d}[/tex] pontas.
Vejamos um exemplo.
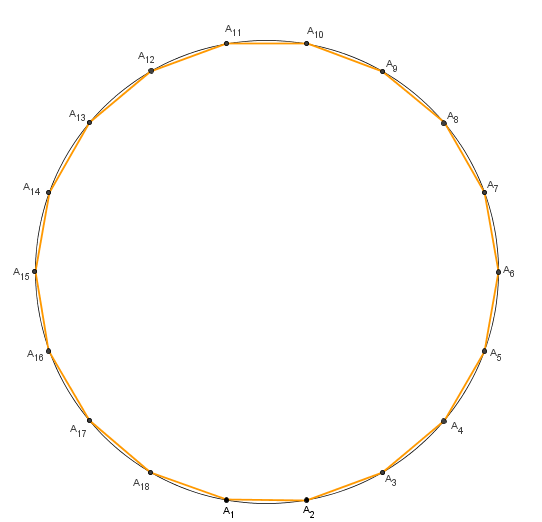
Para tanto tomemos n = 18 e façamos saltos de t em t, com 0 < t < 10.
- t = 1
A figura (18 , 1), assim como a figura (18 , 17), é um polígono regular de 18 lados.
- t = 2
Como 2 é divisor de 18, então a figura (18 , 2), assim como a figura (18 , 16), é um polígono regular de 9 lados.
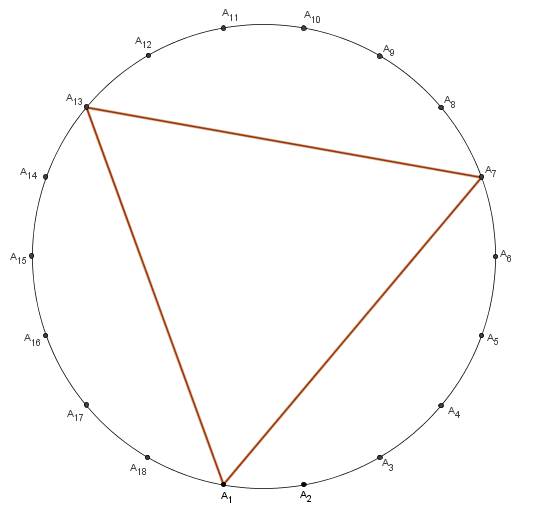
- t = 3
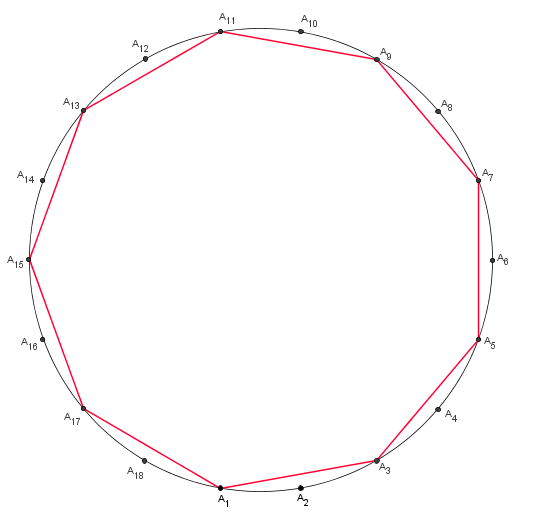
Como 3 é divisor de 18, então a figura (18 , 3), assim como a figura (18 , 15), é um polígono regular de 6 lados.
- t = 4
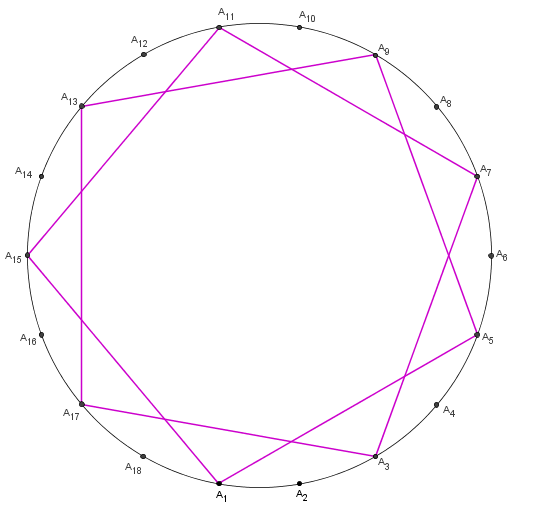
Como d = mdc(18 , 4) = 2 ≠ 1 e 4 não é divisor de 18, então a figura (18 , 4), assim como a figura (18 , 14), é uma estrela de 9 pontas.
- t = 5
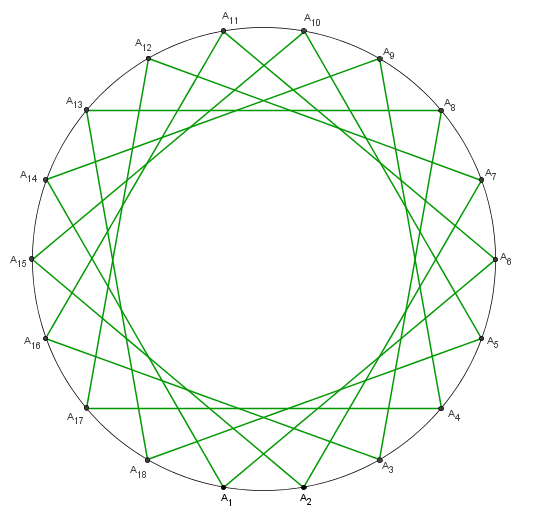
Como d = mdc(18 , 5) = 1, então a figura (18 , 5), assim como a figura (18 , 13), é uma estrela de 18 pontas.
- t = 6
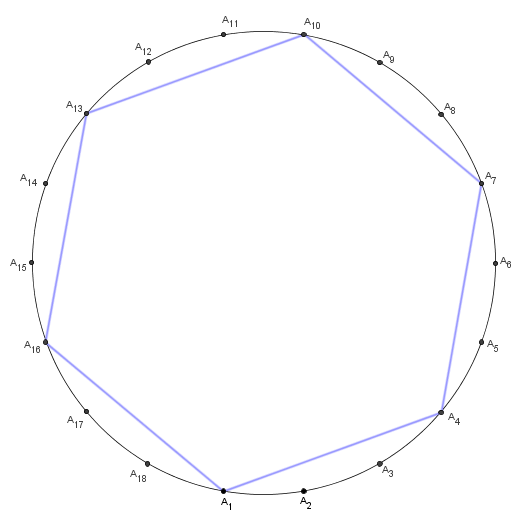
Como 6 é divisor de 18, então a figura (18 , 6), assim como a figura (18 , 12), é um polígono regular de 3 lados.
- t = 7
Como d = mdc(18 , 7) = 1, então a figura (18 , 7), assim como a figura (18 , 11), é uma estrela de 18 pontas.
- t = 8
Como d = mdc(18 , 8) = 2 ≠ 1 e 8 não é divisor de 18, então a figura (18 , 8), assim como a figura (18 , 10), é uma estrela de 9 pontas.
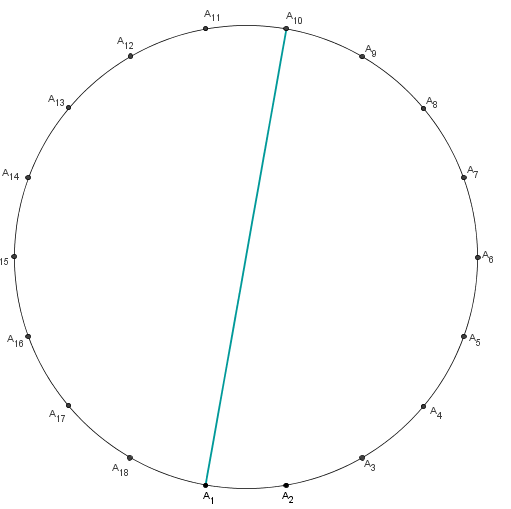
- t = 9
Como 9 = 18 / 2, então a figura (18 , 9) é um segmento de reta.
 |
Finalmente, revelado o mistério e muito mais . . . |
 |
Definimos Estrela, um objeto geométrico, com a ajuda do Máximo Divisor Comum de dois números. |
Equipe COM – OBMEP