✏ Link da Sala para dispositivos da Apple.
UM POUCO DE HISTÓRIA
Uma das figuras do período inicial da Matemática grega mais lembradas nos dias de hoje é, sem dúvida, Pitágoras. Segundo o que se sabe, Pitágoras fundou uma irmandade de interesses filosóficos, científicos e religiosos: a irmandade dos Pitagóricos.
Pitágoras e Pitagóricos,
pormenor d’A escola de Atenas de Rafael (1509).
Pitágoras e sua irmandade defendiam que todas as coisas são números e o princípio fundamental de tudo seria a estrutura numérica. Acredita-se que a filosofia da irmandade se baseava no lema "Tudo é número", ou seja, número seria a substância de todas as coisas.
Os membros dessa irmandade atribuíam todas as suas descobertas ao seu fundador e, embora se trate de figura imprecisa historicamente, já que ele nada deixou escrito, os filósofos Filolaus de Crotona (470a.C.-385 a.C.) e Platão (428 a.C.-347 a.C.) fazem referências à Escola Pitagórica. Mais recentemente, o filósofo e matemático Bertrand Russell classificou Pitágoras como "um dos maiores homens de todos os tempos".
Os Pitagóricos tinham como característica a investigação intensiva e a fundo dos números. A representação física ou geométrica dos números naturais por pontos do plano era uma marca da escola Pitagórica no estudo das propriedades dos números representados e, dentre os vários tipos de números estudados por eles, estavam os chamados números figurados.
Números figurados são números que podem ser representados por um conjunto de pontos do plano com organização padronizada, de modo a formar uma figura geométrica, como por exemplo os números triangulares e os quadrados. Na figura abaixo, são exibidos alguns números desse tipo.
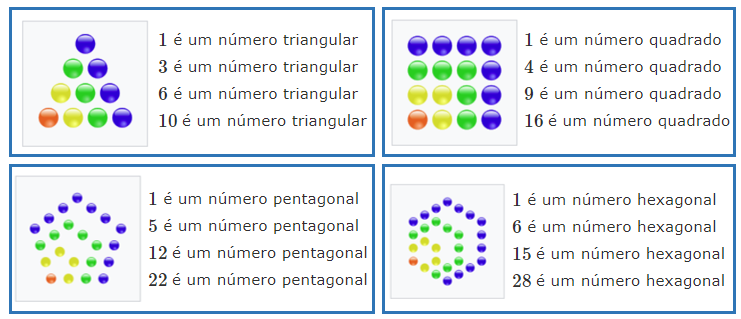Números figurados. Imagens extraídas da Wikipedia
Pesquisas recentes alegam, inclusive, que o Teorema de Pitágoras, no seio da sociedade Pitagórica, pode não ter sido concebido com relação a medidas em um triângulo. Estudos indicam que ele seria um resultado sobre números figurados (sugerimos a aula da referência [3] para que você possa conhecer um pouco mais sobre esta parte da História da Matemática). Nesse contexto, o lema "Tudo é número" significaria que os Pitagóricos conseguiam entender coisas da natureza a partir das configurações numéricas dadas pelos números figurados.
NÚMEROS TRIANGULARES
Os números triangulares estão entre os mais famosos números figurados da história e, provavelmente, perdem em fama apenas para os chamados números quadrados.
Chamamos de triangulares todos os números que podem ser escritos como a soma de uma sequência de naturais consecutivos começando pelo [tex]1[/tex]. Assim, por exemplo:
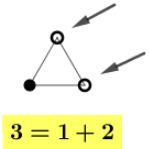
- o número [tex]3[/tex] é triangular, porque [tex]3 = 1 + 2[/tex];
- o [tex]6[/tex] também é triangular, porque [tex]6 = 1 + 2 + 3[/tex];
- o número [tex]10[/tex] também é triangular, já que [tex]1 + 2 + 3 + 4 = 10[/tex];
- [tex]15[/tex] é mais um número triangular, pois [tex]1 + 2 + 3 + 4 + 5 = 15[/tex].
Mas por que chamar estes números de triangulares?
A nomenclatura "Números Triangulares" se deve ao fato de tais números poderem ser representados por pontos do plano arranjados na forma de triângulos equiláteros, com exceção do número [tex]1[/tex], que é definido como o primeiro número triangular por conveniência.
Observe na figura a seguir a representação geométrica clássica dos cinco primeiros números triangulares.
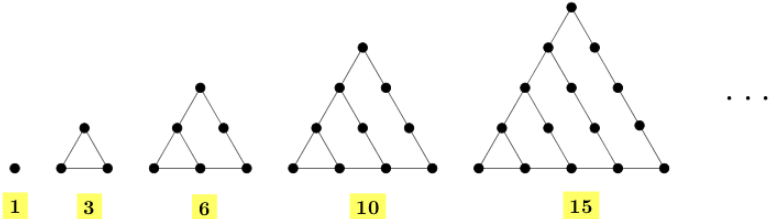
É comum utilizarmos a notação [tex]T_n[/tex] para o [tex]n[/tex]-ésimo número triangular. Assim, por exemplo, [tex]T_1=1[/tex] e [tex]T_2=3[/tex].
Pelo que foi até agora apresentado, uma pergunta natural seria: Qual é o sexto número triangular?
Numericamente, o sexto número triangular é definido pela soma [tex]1 + 2 + 3 + 4 + 5 +6=15+6=21[/tex]. Geometricamente, podemos visualizar [tex]T_6=21[/tex] mantendo o padrão de construção de [tex]T_1[/tex], [tex]T_2[/tex], [tex]T_3[/tex], [tex]T_4[/tex] e [tex]T_5[/tex]; observe:
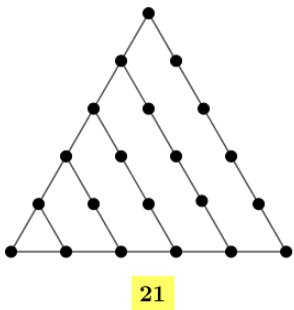
A maneira prática com que obtivemos os primeiros números triangulares precisa ser melhorada, pois como calcularíamos ou representaríamos geometricamente o centésimo número triangular? E o milésimo?
Vamos buscar generalizações para poder responder esse tipo de pergunta e para isso construiremos com cuidado, numérica e geometricamente, a sequência dos números triangulares. Para a figura inicial, utilizaremos um ponto (círculo):
Os números triangulares são os que podem ser representados por meio de triângulos equiláteros. Assim, para construirmos a sequência destes números, construiremos triângulos equiláteros de lados [tex]1, 2, 3[/tex] etc., de maneira que cada nova figura contenha a anterior e acrescente uma unidade à medida de cada lado. Será como ir construindo, aos poucos, uma malha triangular.
Para construir um triângulo, são necessários três vértices. Então, precisamos de mais dois pontos para o segundo número triangular. Junto com o primeiro, estes farão o papel de “vértices”. Observe:
Continuando o processo, a terceira figura será formada pelos pontos da figura anterior e mais três pontos. De fato, construiremos inicialmente um triângulo equilátero com o lado uma unidade maior do que o lado do triângulo da figura anterior. Nessa figura, os dois novos círculos mostrados na imagem central serão vértices desse triângulo. O terceiro círculo será o ponto médio do lado construído. Veja:
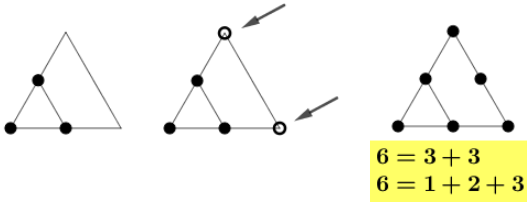
A próxima imagem mostra que com mais quatro círculos acrescentados à figura construída para o terceiro número triangular obtemos o quarto número triangular.
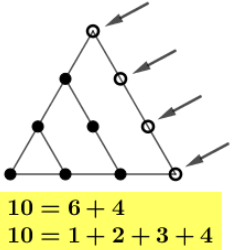
Você deve ter observado a relação aditiva entre os termos consecutivos dessa sequência. Para o [tex]n[/tex]-ésimo número triangular, precisamos adicionar [tex]n[/tex] pontos ao número triangular anterior. É possível escrever esta relação na forma de uma recorrência. (Uma recorrência é, basicamente, um conjunto de regras que permitem calcular os termos de uma sequência em função do(s) seu(s) antecessor(es) imediato(s). Para entender melhor, convidamos você para uma visita à sala Recorrências do nosso Blog).
No nosso caso, a recorrência é bem simples: [tex]\boxed{T_{n}=T_{n-1}+n}.[/tex] Por exemplo, [tex]T_5=T_4+5=10+5=15.[/tex]
Contudo, ao tentarmos calcular números triangulares maiores, esta fórmula não é muito útil. Veja, por exemplo, que para calcularmos o triangular [tex]T_{100}[/tex], precisamos de [tex]T_{99}[/tex], já que [tex]T_{100}=T_{99}+100[/tex]. Mas [tex]T_{99}=T_{98}+99 [/tex] e, portanto, precisamos do valor de [tex]T_{98}[/tex] que, para ser obtido pela nossa fórmula, será necessário o valor de [tex]T_{97}[/tex] E, para o [tex]T_{97}[/tex], é necessário o [tex]T_{96}[/tex]; para o [tex]T_{96}[/tex] é necessário o [tex]T_{95}[/tex]… Inviável, não é?
Tentaremos, então, encontrar uma fórmula não recursiva para os números triangulares. Vamos montar uma tabela com alguns números triangulares para deixar a ideia mais clara e voltar à definição inicial que demos aos números triangulares: números que podem ser escritos como a soma de uma sequência de naturais consecutivos começando pelo [tex]1[/tex]:
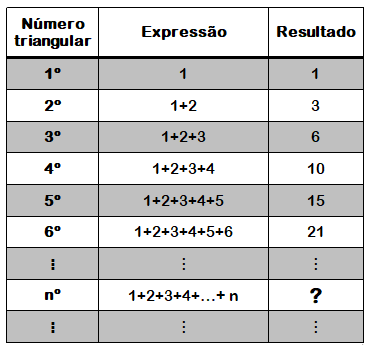
Assim, o que precisamos é obter uma maneira de se calcular a soma [tex]1+2+3+\cdots +(n-1)+n[/tex], para [tex]n[/tex] um número natural não nulo, tenha ele o tamanho que tiver! Para obter uma expressão para essa soma, você pode pensar como o brilhante matemático GAUSS.
Veja a seguir.
[tex]
\;\begin{align*} &1+2+3 \cdots+t= \\
&={\color{red}{1}}+{\color{#1E90FF}{2}}+{\color{#FF8C00}{3}}+{\color{#32CD32}{4}}+ \cdots+{\color{#32CD32}{(t-3)}}+{\color{#FF8C00}{(t-2)}}+{\color{#1E90FF}{(t-1)}}+{\color{red}{t}}\\
&=\underbrace{{\color{red}{[1+t]}}+{\color{#1E90FF}{[2+(t-1)]}}+{\color{#FF8C00}{[3+(t-2)]}}+{\color{#32CD32}{[4+(t-3)]}}+ \cdots+\left[\dfrac{t}{2}+\left(\dfrac{t}{2}+1\right)\right]}_{\frac{t}{2} \, parcelas}\\
&=\underbrace{[1+t]+[1+t]+[1+t]+[1+t]+ \cdots+[1+t]}_{\frac{t}{2} \, parcelas}\\
&=\dfrac{t}{2}\cdot (1+t)\\
&=\boxed{\dfrac{(1+t)\cdot t}{2}}. \end{align*} [/tex]
[tex] \;\begin{align*}& 1+2+3 \cdots+t=\\
&= {\color{red}{1}}+{\color{#1E90FF}{2}}+{\color{#FF8C00}{3}}+ \cdots+{\color{#FF8C00}{(t-2)}}+{\color{#1E90FF}{(t-1)}}+{\color{red}{t}}\\
&=\underbrace{{\color{red}{[1+t]}}+{\color{#1E90FF}{[2+(t-1)]}}+{\color{#FF8C00}{[3+(t-2)]}}+ \cdots+{\color{#32CD32}{\left[\dfrac{t-1}{2}+\dfrac{t+3}{2}\right]}}}_{\frac{t-1}{2} \, parcelas}+\dfrac{t+1}{2}\\
&=\underbrace{[1+t]+[1+t]+[1+t]+[1+t]+ \cdots+[1+t]}_{\frac{t-1}{2} \, parcelas}+\dfrac{t+1}{2}\\
&=\dfrac{t-1}{2}\cdot (1+t)+\dfrac{1+t}{2}\\
&=\boxed{\dfrac{(1+t)\cdot t}{2}}. \end{align*}[/tex]
Para mais detalhes, visite a sala A soma 1 + 2 + 3 + … + t. E não deixe de ouvir a história do menino Gauss!
Unindo a observação da tabela à soma encontrada pelo método de Gauss, conclui-se que o [tex]n-[/tex]ésimo número triangular pode ser obtido utilizando-se a fórmula [tex]\, \fcolorbox{#6495ED}{#ffffff}{$\,T_n=\dfrac{(1+n)\cdot n}{2}=\dfrac{n+n^2}{2}\,$}\,[/tex].
[tex]\qquad T_6=\dfrac{6+6^2}{2}=21[/tex]
e até calcular [tex]T_{100}[/tex]:
[tex]\qquad T_{100}=\dfrac{100+100^2}{2}=5050[/tex].
PROPRIEDADES E CURIOSIDADES
Os números triangulares possuem propriedades muito interessantes, dentre as quais destacamos as seguintes:
Formalmente, um número natural [tex] n,\,n\gt1[/tex], chama-se perfeito se for igual à soma de seus divisores naturais próprios (isto é, divisores menores do que [tex]n[/tex]). Por exemplo, o número [tex]6[/tex] é perfeito, porque o conjunto dos divisores naturais próprios de [tex]6[/tex] é [tex]\{1,2,3\}[/tex] e temos [tex]1+2+3=6[/tex].
Uma interessante propriedade é a de que todo número perfeito par é triangular (e também hexagonal).
(Fica o convite para uma visita à nossa sala sobre Números Perfeitos.)
Para visualizar esta propriedade, desenhe os números triangulares como triângulos retângulos e faça a "montagem" exemplificada abaixo:
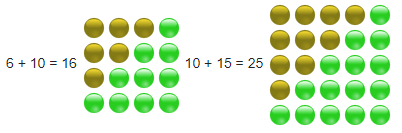Números triangulares consecutivos formando um quadrado.
Fonte: Wikipédia
[tex]\qquad ST_n=\left( \dfrac{(3 + 2\sqrt{2})^n- (3 – 2\sqrt{2})^n}{4\sqrt{2}} \right)^2. [/tex]
Observe que
[tex]\qquad ST_1=\left( \dfrac{(3 + 2\sqrt{2})^1- (3 – 2\sqrt{2})^1}{4\sqrt{2}} \right)^2=\left( \dfrac{4\sqrt{2}}{4\sqrt{2}} \right)^2 =1[/tex],
como esperado.
Se você entende um pouco de inglês, a referência [2] é uma excelente leitura.
Em símbolos:
[tex]\qquad \qquad T_n^2=1^3+2^3+\cdots + n^3.[/tex]
Há uma prova visual muito interessante deste fato, para [tex]n=5[/tex]:
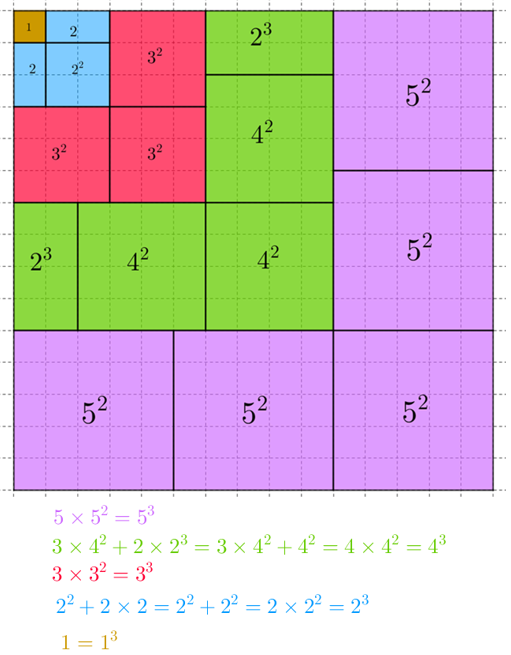
A figura mostra um quadrado de lado [tex]1[/tex], dois quadrados de lados [tex]2[/tex] (o equivalente, em valor numérico de área, ao valor numérico de volume de um cubo [tex]2\times 2 \times 2[/tex]), três quadrados de lados [tex]3[/tex] (o equivalente a um cubo [tex]3\times 3 \times 3[/tex]) e assim por diante. Alguns quadrados são partidos em dois retângulos para que o encaixe fique perfeito.
Observe que a área total é a soma dos cubos consecutivos. Acompanhando a borda superior da figura, temos [tex]1+2+3+4+5[/tex], ou seja, a soma dos números consecutivos. Mas a área total é o quadrado da medida do lado! Assim:
[tex]\qquad \qquad 1^3+2^3+3^3+4^3+ 5^3=(1+2+3+4+5)^2=T_5^2.[/tex]
Utilizando a próxima figura e a ideia de volume propriamente dita, podemos comparar o volume da placa colorida com o volume total das cinco pilhas de quadradinhos e obter que:
[tex]\qquad 1^3+2^3+3^3+4^3+5^3=(1+2+3+4+5)^2\times 1\\
\qquad 1^3+2^3+3^3+4^3+5^3=(1+2+3+4+5)^2=T_5^2.[/tex]
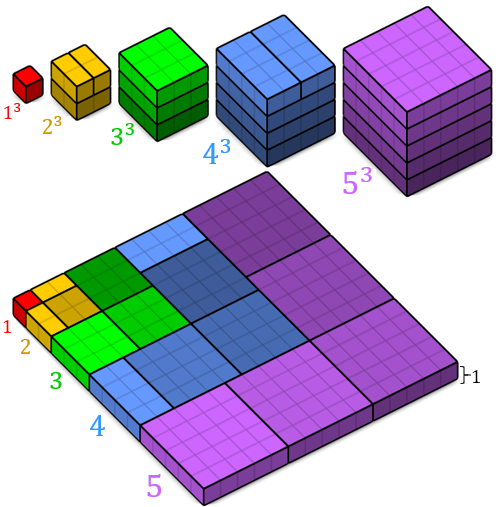Adaptado da Wikipédia
(6) Em 1798, o matemático alemão Carl Friedrich Gauss provou a conjectura do matemático francês Pierre de Fermat (1607-1665) de que todo inteiro positivo pode ser representado pela soma de três números triangulares, escrevendo em seu diário sua famosa observação:
[tex]\epsilon \, \upsilon \, \rho\, \eta \, \kappa \, \alpha [/tex][tex]\text{! NUM}=\Delta+\Delta+\Delta[/tex].
Para Gauss, essa demonstração foi tão importante que ele saudou a propriedade com a exclamação arquimediana "EUREKA!" em grego: [tex]\,\boxed{\,\epsilon \, \upsilon \, \rho\, \eta \, \kappa \, \alpha ! \,}\,[/tex].
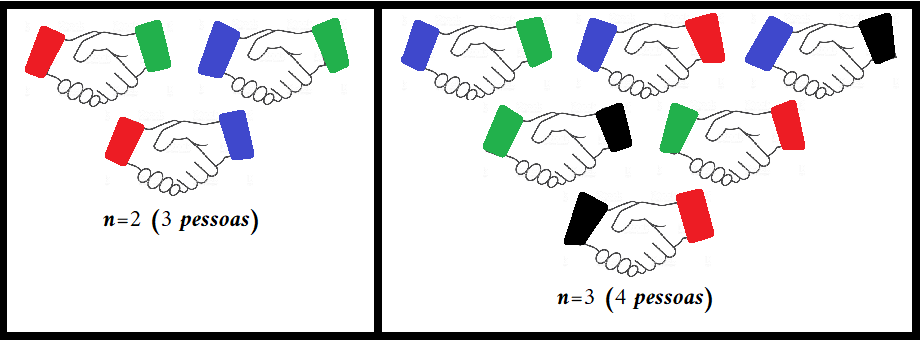
Assim, não existem quatro números triangulares em progressão geométrica.
Em uma tabuada convencional, os dobros dos números triangulares aparecem paralelamente à diagonal dos números quadrados perfeitos:
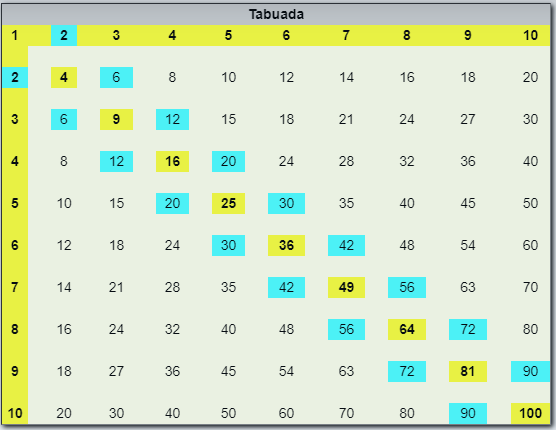A tabuada e os números triangulares.
Além disso, a soma de um número quadrado perfeito com um número à sua esquerda ou à sua direita é um número triangular. Por exemplo, [tex]25+20=45[/tex] é um número triangular, assim como [tex]25+30=55[/tex].
Imagem extraída de Freepik
Pois bem, é possível explorar os números triangulares por meio de "pilhas":
Números triangulares como pilhas.
Fonte: Instrumentação do Ensino da Aritmética e da Álgebra – Vol.1.
Entretanto, essa visualização pode não ser possível para outros números poligonais, como, por exemplo, os números pentagonais. Por isso, não a utilizamos aqui.
VÍDEOS PARA APRENDER MAIS
Números triangulares e quadrados perfeitos
No vídeo abaixo, o Prof. Rafael Procópio oferece uma prova algébrica para a propriedade 3: a soma de dois números triangulares consecutivos resulta em um número quadrado.
Números triangulares
No vídeo abaixo, é mostrada uma representação dinâmica dos cinco primeiros números triangulares.
Sequências de Números Triangulares
A playlist abaixo apresenta dez pequenas aulas sobre sequências numéricas, com ênfase em Sequências de Números Triangulares. Os exercícios resolvidos fazem com que esta seja uma boa pedida para quem está, por exemplo, treinando para vestibulares.
ATIVIDADES
Dica inicial: Use que todo inteiro da forma [tex]8n+3[/tex] pode ser escrito como a soma de três quadrados e tente provar que estes quadrados devem ser todos ímpares. Caso haja dúvidas, não hesite em procurar seus professores ou a nossa equipe!
Equipe COM – OBMEP
[1] Ciências sem Dúvidas. Pré-Socráticos – A Escola Pitagórica. (Último acesso em 15/05/20)
[2] Math Pages. Square Triangular Numbers. (Último acesso em 15/05/20)
[3] Mestrado PROFMAT-Tópicos de História da Matemática. A matemática Grega antes de Euclides. (Último acesso em 15/05/20)
[4] OLIVERO, Mário Instrumentação do Ensino da Aritmética e da Álgebra – Vol.1. Consórcio
CEDERJ/UENF/UERJ/UFF/UFRJ/UFRRJ/UNIRIO/Fundação CECIERJ, 2010
[5] Pequena Galeria de Grandes Matemáticos: Johann Carl Friedrich Gauss. (Último acesso em 15/05/20)
[6] Pequena Galeria de Grandes Matemáticos: Pitágoras de Samos. (Último acesso em 15/05/20)
[7] SILVA, Ana Lúcia Vaz da; VAIANO, Andréa Zander; BARBOSA, Andreia Carvalho Maciel; BAIRR, Marcelo Almeida. Instrumentação do Ensino da Aritmética e da Álgebra – Vol.1. Consórcio CEDERJ/UENF/UERJ/UFF/UFRJ/UFRRJ/UNIRIO/Fundação CECIERJ, 2010
[8] SILVA, Ricardo. Os fantásticos números primos – Tabuada e os números triangulares. (Último acesso em 15/05/20)
[9] STEWART, Ian. Os mistérios matemáticos do professor Stewart. Rio de Janeiro: Zahar, 2015.
[10] STRATHERN, Paul. Pitágoras e seu Teorema em 90 minutos. Rio de Janeiro: Jorge Zahar ed., 1998.
[11] WIKIPÉDIA. Número figurado. (Último acesso em 15/05/20)