.Sala de Estudo: Malabarismos aritméticos e algébricos

Algébricos e Aritméticos

Aritmética x Álgebra

A briga eterna na cabeça de quem está aprendendo Matemática…

O contato inicial de quem está aprendendo Matemática com a Álgebra é um momento de ruptura com a matemática “concreta” da Aritmética, para uma entrada na matemática “abstrata” da Álgebra!
Na Aritmética, números são números e na Álgebra, números são letras, isso porque enquanto que na Aritmética há uma busca por um resultado final, “um número de verdade”, na Álgebra, o foco é estabelecer procedimentos e relações para expressá-los de forma geral e simplificada. Na Álgebra procuramos expressar o que é genérico, ou seja, aquilo que se pode afirmar não apenas para um único número, mas sim para muitos e muitos valores numéricos, independentemente de quais sejam.
Particularmente para aqueles que acreditam que em um problema de matemática deve-se, necessariamente, encontrar uma resposta numérica, a Álgebra é um verdadeiro terror, já que a resposta de um problema algébrico deve expressar, de alguma forma, o processo a ser realizado para a resolução do problema.
Muitas vezes, quem está resolvendo um problema de Álgebra até entende que tem que somar dois números [tex]a \, [/tex] e [tex] \, b[/tex], mas fica incrédulo que a resposta seja [tex]a+b \, [/tex]. Assim, não é raro, que em situações como essa, a soma [tex]3x+5y[/tex] seja efetuada e resulte em [tex]8xy[/tex].
Nesta Sala de Estudos queremos propor problemas que envolvem Identidades Algébricas, já que estas são ferramentas extremamente úteis em diversos cálculos matemáticos. No entanto, gostaríamos que vocês apreciassem a beleza dos problemas que serão propostos (muitos deles extraídos de Olimpíadas realizadas em várias partes do mundo), e, também, conseguissem resolvê-los. Mas, para isso é necessário que vocês conheçam algumas Identidades Algébricas e também tenham certeza de que não cometem “erros algébricos” como o que comentamos, [tex]3x+5y=8xy[/tex], ou mesmo erros em manipulações aritméticas.
Assim, lhes oferecemos três opções, não excludentes:

✽ ir para a página na qual apresentaremos alguns erros algébricos e aritméticos que são cometidos com frequência na resolução de problemas (Sala 1);
✽ ir para a página na qual exploraremos algumas identidades algébricas (Sala 2);
✽ ir para a página na qual apresentaremos os problemas (Sala 3).

Bem, ir para uma ou outra página é fácil, basta clicar no botão conveniente. Mas tomar a decisão de qual botão deve ser clicado pode ser bem mais complicado!

Você ficou na dúvida se já cometeu ou ainda comete erros algébricos?
Não tem certeza de que sabe o que é uma identidade algébrica?

Então resolva o problema-teste abaixo e avalie se você deve ou não ir diretamente para a página de problemas.

De qualquer forma, independente do botão escolhido,
Bons Estudos!

Problema-teste

---

Em certa Mostra de Invenções, as atenções se voltaram para interessantes robôs de desinfecção hospitalar.
Um dos inventores apresentou o robô JLZM e um segundo inventor apresentou os robôs NZM e TZM.

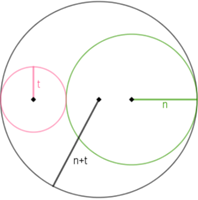
● Os robôs NZM e TZM trabalham juntos e desinfetam, respectivamente, áreas circulares de raios [tex]n \, [/tex] e [tex] \, t[/tex], a cada período de tempo [tex]p[/tex].
● O robô JLZM desinfeta, no mesmo período de tempo [tex]p[/tex], uma área circular de raio [tex]n+t[/tex].

Sabendo que o custo de JLZM é a soma dos custos de NZM e TZM, qual das alternativas abaixo lhe parece correta?

Escolha a alternativa e faça uma avaliação da sua resposta!

a) Valerá mais a pena produzir robôs NZM e TZM. Infelizmente não é esta a alternativa correta! Ao resolver algebricamente o problema, você se depara com uma expressão do tipo [tex]\left( x+y \right)^2[/tex]. Um erro comum é acreditar que [tex]\left( x+y \right)^2=x^2+y^2[/tex], o que não é correto. O que é verdadeiro é a identidade algébrica [tex]\qquad \left( x+y \right)^2=x^2+2xy+y^2[/tex]. Recomendamos que você dê uma passadinha nas Salas 1, 2 e 3.

b) Valerá mais a pena produzir robôs JLZM. Parabéns! Esta é a alternativa correta! Ao resolver o problema, você utilizou álgebra ou pensou na figura abaixo e tirou a sua conclusão? De qualquer forma, confira a resposta e passe pelas Salas 1 e 2 antes de ir para a Sala 3. Quem sabe você não aprende alguma coisinha nova…

c) Não há diferença: ambos os inventores produziram projetos de limpeza de mesmo custo/benefício. Infelizmente não é esta a alternativa correta! Ao resolver algebricamente o problema, você se depara com uma expressão do tipo [tex]\left( x+y \right)^2[/tex]. Um erro comum é acreditar que [tex]\left( x+y \right)^2=x^2+y^2[/tex], o que não é correto. O que é verdadeiro é a identidade algébrica [tex]\qquad \left( x+y \right)^2=x^2+2xy+y^2[/tex]. Recomendamos que você dê uma passadinha nas Salas 1, 2 e 3.

d) É impossível dizer qual tipo de robô deve ser escolhido sem saber os valores de [tex]n[/tex] e [tex]t[/tex]. Infelizmente não é esta a alternativa correta! Você se lembra do que falamos sobre a Álgebra no início desta página? Pois é, utilizando ferramentas algébricas é possível manipularmos equações e expressões definidas a partir de números que não conhecemos! A Álgebra está presente na resolução de problemas nos quais não importa o valor desses números desconhecidos e este é um desses problemas! Veja abaixo a solução e visite as Salas 1, 2 e 3.

Inicialmente, lembramos que a área de um círculo de raio r é [tex]\pi r ^2[/tex]. Logo, a área desinfetada por NZM e TZM, a cada período de tempo, é dada por [tex]\pi n^2+\pi t^2=\pi(n^2+t^2)[/tex].
Por outro lado, a área desinfetada por JLZM, no mesmo período de tempo, é [tex]\pi (n+t)^2[/tex].
Como a constante [tex]\pi[/tex] é comum às duas expressões, a questão, agora é: que número é maior? [tex](n+t)^2[/tex] ou [tex]n^2+t^2[/tex]?
Uma importante identidade algébrica garante que [tex](n+t)^2= n^2+2nt+t^2.[/tex]
Por outro lado, como [tex]n[/tex] e [tex]t[/tex] são números positivos, isto é, [tex]n \gt 0[/tex] e [tex]t \gt 0[/tex], então [tex]2nt \gt 0 [/tex], donde [tex] n^2+2nt+t^2 \gt n^2+ t^2.[/tex]
Portanto, [tex]\pi(n^2+t^2)<\pi(n+t)^2[/tex] e, assim, valerá mais a pena a produção dos robôs JLZM, que desinfetarão, com o mesmo custo e no mesmo tempo, uma área maior que as desinfetadas pelos robôs NZM e TZM.

Ainda na dúvida?
Precisam de mais um problema para decidir?
Aí vai……

Um segundo problema

---

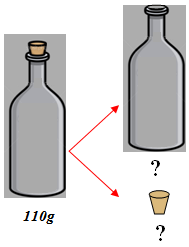
A Garrafa e a rolha

Uma garrafa com sua rolha pesam juntas 110 gramas.
Sabendo que a garrafa pesa 100 gramas a mais que a rolha, qual é o peso da rolha?

Se você respondeu que a rolha pesa [tex]10[/tex] gramas, você foi mais uma dentre as pessoas que erraram a resposta. Diga-se, de passagem, que a maioria das pessoas que fazem este problema erram a resposta… Observe que se a rolha pesasse [tex]10[/tex] gramas, a garrafa pesaria [tex]100[/tex] gramas, ou seja, [tex]100-10=90[/tex] gramas a mais do que a rolha e não [tex]100[/tex] gramas como pede o problema. Viu a confiança exagerada em números verdadeiros? Se você pensasse algebricamente e não cometesse erros grosseiros, fatalmente chegaria na resposta correta. Vejamos… Sejam [tex]G[/tex] o peso da garrafa, em gramas, e [tex]R[/tex] o peso da rolha, também em gramas. Assim, como juntas a garrafa e a rolha pesam [tex]110 \, g[/tex], então [tex]\qquad G + R = 110. \qquad \qquad (i)[/tex] Por outro lado, a garrafa pesa [tex]100[/tex] gramas a mais que a rolha, então [tex]\qquad G = R + 100. \qquad \qquad(ii)[/tex] Por [tex](i)[/tex] e [tex](ii)[/tex] temos que [tex]\qquad \left(R + 100\right)+R=110[/tex] [tex]\qquad 2R=110-100[/tex] [tex]\qquad 2R=10[/tex] [tex]\qquad R=5[/tex]. Assim [tex]R=5[/tex], [tex]G=105[/tex] e [tex]G-R=105-5=100[/tex]. Será que não seria bom você dar uma passadinha nas Salas 1 e 2 antes de ir para a Sala 3 ?

Agora é a hora da decisão…

Equipe COM – OBMEP