✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Muito Difícil)
Na figura, os pontos [tex]A, \, C, \, F[/tex] são colineares, assim como os pontos [tex]A, \, B, \, D[/tex] .
Sabendo-se que o triângulo retângulo [tex]BCA[/tex] tem a mesma área do retângulo [tex]BDEF[/tex] e que os comprimentos dos segmentos [tex]\overline{BC} \, [/tex] e [tex] \, \overline{BF}[/tex] são, respectivamente, [tex]6 \, cm \, [/tex] e [tex] \, 7 \, cm[/tex], determinar a distância do ponto [tex]E \, [/tex] à semirreta [tex]r \, .[/tex]
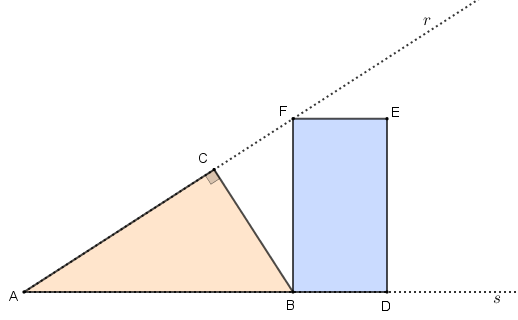
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].

Lembretes
(1) Ângulos correspondentes definidos por retas paralelas têm a mesma medida. (Se você não se lembra dos ângulos correspondentes, clique AQUI.)
(2) A medida de um ângulo externo a um triângulo qualquer é a soma das medidas dos ângulos internos do triângulo que não são adjacentes a ele. (Se você não se lembra desse resultado, clique AQUI.)
Solução
Sejam [tex]P[/tex] o pé da perpendicular à reta [tex]r[/tex] traçada a partir do ponto [tex]E[/tex] e [tex]\theta[/tex] a medida em graus do ângulo [tex]B\hat{A}C \, [/tex], conforme ilustra a figura abaixo, na qual também indicamos as medidas dos segmentos [tex]\overline{BC} \, [/tex] e [tex] \, \overline{BF} \, .[/tex]
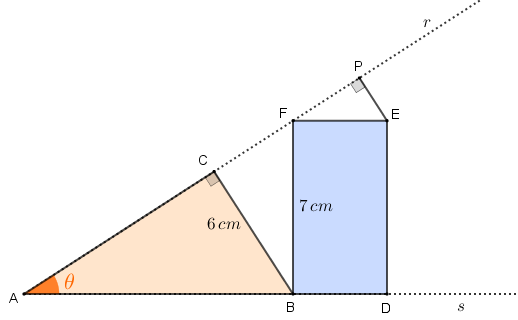
Para determinar a distância do ponto [tex]E \, [/tex] à semirreta [tex]r \, [/tex], vamos, então calcular o comprimento do segmento [tex]\overline{PE} \, .[/tex] Para isso, observe inicialmente que:
- os segmentos [tex]\overline{AB} \, [/tex] e [tex] \, \overline{FE}[/tex] são paralelos; logo, os ângulos [tex]B\hat{A}C \, [/tex] e [tex]E\hat{F}P \, [/tex] são correspondentes. Portanto, pelo Lembrete (1), a medida de [tex]E\hat{F}P \, [/tex] é também [tex]\theta \, .[/tex]
Vamos determinar, agora, a medida em graus do ângulo [tex]F\hat{B}C \, [/tex], a qual inicialmente denotaremos por [tex]b \, .[/tex]
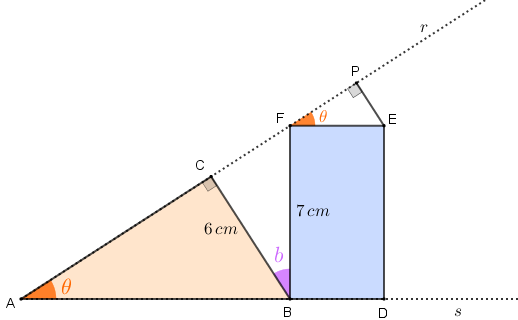
- Perceba que [tex]C\hat{B}D \, [/tex] é um ângulo externo ao triângulo [tex]ABC[/tex] e tem medida igual a [tex]b+90^\circ \, [/tex]; assim, pelo Lembrete (2), temos que [tex]b+90^\circ=\theta+90^\circ \, [/tex], donde [tex]b=\theta \, .[/tex]
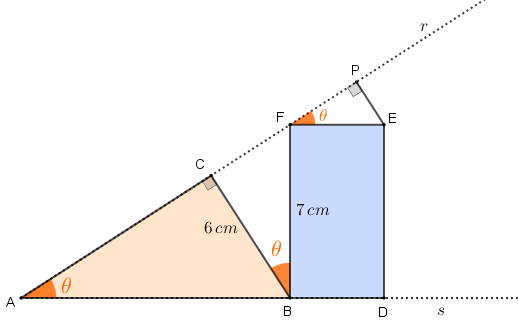
Com os dados que aparecem na figura acima, já estamos em condições de determinar a distância de [tex]E \, [/tex] à [tex]r \, .[/tex] Vamos lá!
A partir dos triângulos retângulos [tex]BAC \, [/tex] e [tex] \, EFP \, [/tex], podemos obter, respectivamente, as seguintes relações:
[tex]\qquad \qquad \boxed{tg \, \theta=\dfrac{BC}{AC}=\dfrac{6}{AC}}, \, \, \textcolor{#800000}{(i)}\qquad[/tex] e [tex]\qquad \boxed{sen \, \theta= \dfrac{PE}{FE}}, \, \, \textcolor{#800000}{(ii)} \, .[/tex]
Por outro lado, uma das hipóteses do problema nos assegura que o triângulo retângulo [tex]BCA[/tex] tem a mesma área do retângulo [tex]BDEF[/tex]; assim, indicando essas áreas respectivamente por [tex]\textcolor{#f93}{[BCA]} \, [/tex] e [tex] \, \textcolor{#6699FF}{[BDEF]} \, [/tex], segue que:
[tex]\qquad \textcolor{#f93}{[BCA]}=\textcolor{#6699FF}{[BDEF]} \, [/tex]
[tex]\qquad \textcolor{#f93}{\dfrac{AC \times BC}{2}}=\textcolor{#6699FF}{BF \times FE} \, [/tex]
[tex]\qquad \dfrac{AC \times 6}{2}=7 \times FE \, [/tex]
[tex]\qquad \dfrac{\dfrac{6}{tg \, \theta} \cdot 6}{2}\stackrel{\textcolor{#800000}{(i)}}{=}7 \times FE \, [/tex]
[tex]\qquad \dfrac{18}{tg \, \theta}=7 \times FE \, [/tex]
[tex]\qquad\dfrac{18}{tg \, \theta}\stackrel{\textcolor{#800000}{(ii)}}{=}7 \times \dfrac{PE}{sen \, \theta} \, [/tex]
[tex]\qquad PE=\dfrac{18\cdot sen \, \theta}{7\cdot tg \, \theta}=\dfrac{18\cdot sen \, \theta}{7\cdot \dfrac{sen \, \theta}{ \, cos \, \theta} \, }=\dfrac{18\cdot \cancel{sen \, \theta} \cdot cos \, \theta}{7\cdot \cancel{sen\theta}}[/tex]
[tex]\qquad PE=\dfrac{18}{7}\cdot cos \, \theta \, .\quad \textcolor{#800000}{(iii)} \, [/tex]
Mas, observando o triângulo retângulo [tex]BCF \, [/tex], vemos que [tex]cos\, \theta=\dfrac{6}{7}[/tex]; logo, de [tex]\textcolor{#800000}{(iii)} \, [/tex], segue que:
[tex]\qquad PE=\dfrac{18}{7}\cdot \dfrac{6}{7}=\dfrac{108}{49} \, .[/tex]
Portanto, a distância do ponto [tex]E \, [/tex] à semirreta [tex]r \, [/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{108}{49} \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
