.Sala para leitura_025: Família de ângulos

Família de ângulos

Dadas duas retas distintas [tex]r[/tex] e [tex]s[/tex], paralelas ou não, e uma reta [tex]t[/tex] concorrente com [tex]r[/tex] e [tex]s[/tex], que denominamos de transversal, automaticamente fica definida uma família de oito ângulos, conforme ilustra a figura abaixo.

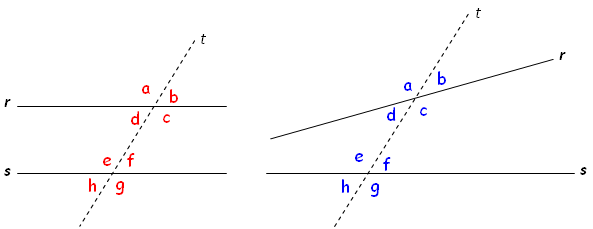
Pares desses ângulos costumam receber nomes particulares, de acordo com a posição de um deles em relação à do outro:

• alternos internos: [tex]\boxed{\,\hat{d} \, \text{ e } \, \hat{f}\,} \, [/tex] ; [tex] \, \boxed{\,\hat{c} \, \text{ e } \, \hat{e}\,} \, .[/tex]
• alternos externos: [tex]\boxed{\,\hat{a} \, \text{ e } \, \hat{g}\,} \, [/tex] ; [tex] \, \boxed{\,\hat{b} \, \text{ e } \, \hat{h}\,} \, .[/tex]
• correspondentes: [tex]\boxed{\,\hat{a} \, \text{ e } \, \hat{e}\,} \, [/tex] ; [tex] \, \boxed{\,\hat{b} \, \text{ e } \, \hat{f}\,} \, [/tex] ; [tex] \, \boxed{\,\hat{d} \, \text{ e } \, \hat{h}\,} \, [/tex] ; [tex] \, \boxed{\,\hat{c} \, \text{ e } \, \hat{g}\,} \, .[/tex]
• opostos pelo vértice: [tex]\boxed{\,\hat{a} \, \text{ e } \, \hat{c}\,} \, [/tex] ; [tex] \, \boxed{\,\hat{b} \, \text{ e } \, \hat{d}\,} \, [/tex] ; [tex] \, \boxed{\,\hat{e} \, \text{ e } \, \hat{g}\,} \, [/tex] ; [tex] \, \boxed{\,\hat{f} \, \text{ e } \, \hat{h}\,} \, .[/tex]

Quando [tex]r[/tex] e [tex]s[/tex] não são retas paralelas, em geral, só conseguimos garantir a congruência entre os dois ângulos que compõem um par de ângulos opostos pelo vértice. (Utilizando a nossa notação, [tex]\hat{a} \, \equiv \hat{c} \, [/tex] ; [tex]\hat{b} \, \equiv \hat{d} \, [/tex] ; [tex]\hat{e} \, \equiv \hat{g} \, [/tex] ; [tex]\hat{f} \, \equiv \hat{h} \, [/tex].) No entanto, quando [tex]r[/tex] e [tex]s[/tex] são retas paralelas, temos apenas duas medidas para os oito ângulos definidos por cada reta transversal, e essas duas medidas somam [tex]180^\circ[/tex].

Fantástico, não é?

Com a ajuda do applet é possível visualizar uma importantíssima propriedade da geometria plana:

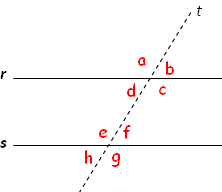
Se [tex]r \, [/tex] e [tex] \, s[/tex] são retas paralelas, então, com base na notação da figura ao lado, temos que:

• ângulos correspondentes são congruentes: [tex]\hat{a} \, \equiv \hat{e} \, [/tex] ; [tex]\hat{b} \, \equiv \hat{f} \, [/tex] ; [tex]\hat{d} \, \equiv \hat{h} \, [/tex] ; [tex]\hat{c} \, \equiv \hat{g} \, [/tex] ;
• ângulos alternos internos são congruentes: [tex]\hat{d} \, \equiv \hat{f} \, [/tex] ; [tex]\hat{c} \, \equiv \hat{e} \, [/tex] ;
• ângulos alternos externos são congruentes: [tex]\hat{a} \, \equiv \hat{g} \, [/tex] ; [tex]\hat{b} \, \equiv \hat{h} \, [/tex] ;
• ângulos opostos pelo vértice são congruentes: [tex]\hat{a} \, \equiv \hat{c} \, [/tex] ; [tex]\hat{b} \, \equiv \hat{d} \, [/tex] ; [tex]\hat{e} \, \equiv \hat{g} \, [/tex] ; [tex]\hat{f} \, \equiv \hat{h} \, [/tex].

Vale a pena registrar que a congruência de apenas um par de ângulos alternos (ou um par de ângulos correspondentes) definidos em duas retas intersectadas por uma transversal garante que essas duas retas são paralelas.

CUIDADO: A congruência de dois ângulos opostos pelo vértice definidos por uma transversal a duas retas dadas NÃO garante que essas duas retas sejam paralelas.

Equipe COM – OBMEP