.Texto_010: Um pouco sobre poliedros

O que são poliedros?

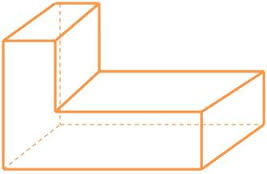
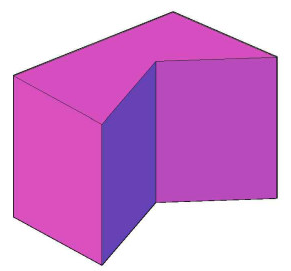
Nesta nossa breve discussão, vamos adotar uma definição de poliedro que, embora não seja muito geral, atende perfeitamente às nossas finalidades. Adotando essa definição, podemos escrever com rigor a ideia intuitiva de que poliedro é um objeto geométrico de três dimensões, formado por polígonos.

Assim, para afirmarmos, neste tópico, que um objeto é um poliedro, teremos que verificar se as condições (a), (b) e (c) são, simultaneamente, cumpridas. Se uma delas falhar, o objeto não pode ser classificado/chamado de poliedro. Nessa altura do campeonato vocês podem estar se perguntando: E os exemplos?
Bom, chegou a hora deles e, portanto, convidamos vocês para a Atividade 1.

Vamos lá? É só clicar no botão abaixo e
bons estudos!

Observem atentamente as 16 figuras abaixo e investiguem se o objeto que cada uma representa atende às condições (a), (b) e (c) da nossa definição de poliedro.

Na análise de cada figura, é claro que:

• se as três condições forem satisfeitas, então a figura representa um poliedro;
• se uma das condições falhar já é suficiente para vocês garantirem que não se trata de um poliedro, e nem seria necessário testar as demais condições.

Mas queremos saber se vocês entenderam, de fato, as três condições, por isso a atividade não é, simplesmente, garantir se temos ou não poliedros, mas sim verificar quais dentre as condições (a), (b) e (c) são válidas e quais não, para cada um dos 16 objetos representados.

Objeto 1	Objeto 2	Objeto 3	Objeto 4
Objeto 5	Objeto 6	Objeto 7	Objeto 8
Objeto 9	Objeto 10	Objeto 11	Objeto 12
Objeto 13	Objeto 14	Objeto 15	Objeto 16

Os poliedros podem ser classificados em várias categorias. A próxima definição trata de uma categoria importante de poliedros: os poliedros convexos.

Dentre os poliedros convexos, destacaremos um tipo conhecido desde a antiguidade e que recebeu tratamento especial no livro XIII dos Elementos de Euclides: os poliedros regulares.

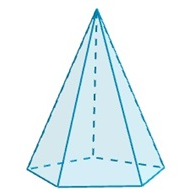
Observem que a segunda condição da definição de poliedro regular não decorre da primeira, como inicialmente poderíamos pensar. A bipirâmide pentagonal, por exemplo, tem dez faces que são triângulos equiláteros, mas o número de arestas que partem de cada vértice dela não é o mesmo (de alguns partem 4 e de outros partem 5). Dessa forma a bipirâmide pentagonal não é um poliedro regular.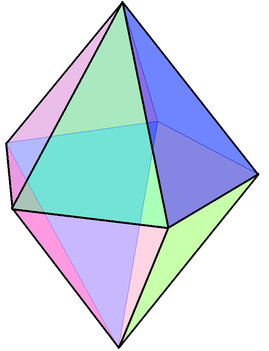

É possível demonstrar que existem apenas cinco tipos de poliedros regulares: os tetraedros, os cubos, os octaedros, os dodecaedros e os icosaedros.

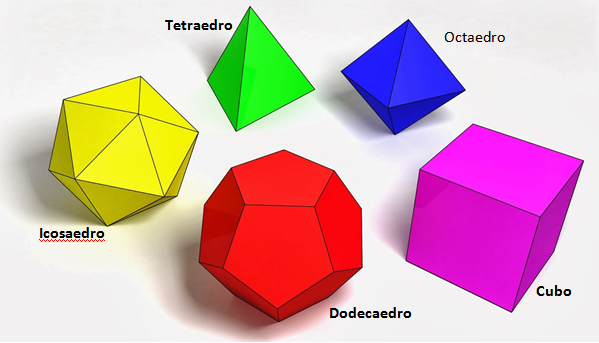
Cabe aqui a observação de que, historicamente, o termo poliedro surgiu para designar o objeto sólido (sólidos de Platão, por exemplo). Atualmente o termo poliedro é utilizado tanto para o sólido como para a sua superfície (nosso caso).

A relação de Euler para poliedros

Apresentaremos agora um importante resultado sobre poliedros, conhecido como Relação de Euler ou Fórmula de Euler ou Teorema de Euler. Trata-se de uma propriedade geral que estabelece uma relação entre o número de vértices, o número de arestas e o número de faces de um poliedro convexo. O resultado foi anunciado pelo grande matemático suíço Leonhard Euler (1707–1783) em uma carta que ele escreveu para seu amigo, o também matemático Christian Goldbach (1690–1764), em novembro de 1750.

Observe que o resultado garante que a relação [tex]V – A + F = 2 [/tex] vale para todo poliedro convexo, mas nada podemos garantir para poliedros não convexos. Embora existam poliedros não convexos para os quais a relação é verdadeira, também existem poliedros não convexos para os quais ela não vale. Particularmente, poliedros para os quais a Relação Euler é válida são chamados poliedros Eulerianos. Assim:

Todo poliedro convexo é Euleriano, mas nem todo poliedro Euleriano é convexo.

Não faremos a demonstração aqui de que a relação de Euler é uma condição necessária para que um poliedro seja convexo, pois isso fugiria do nosso propósito que é, apenas, apresentar informações básicas para uma melhor execução das atividades relacionadas aos caleidociclos. Para os que se interessarem por conhecer uma demonstração desse resultado e explorá-lo um pouco mais, indicamos os seguintes artigos publicados na Revista do Professor de Matemática, RPM, edição número 3 de 1982 e edição número 47 de 2010, respectivamente:

E agora, vamos praticar?

Indo além da relação de Euler . . .

Muitos matemáticos se debruçaram sobre a relação [tex]V – A + F = 2 [/tex] tentando fazer dela um “teorema de verdade“, livre de contraexemplos, por mais de um século. Como frutos de toda essa discussão colhemos a necessidade de uma definição precisa do que seja um poliedro (o próprio Euler nunca definiu precisamente poliedro) e a genial visão de Poincaré de que o número [tex]V – A + F[/tex] é, na verdade, uma característica topológica e não geométrica. Na verdade, ele notou que esse número é um invariante topológico, o que explicaria porque para todos os poliedros convexos [tex]V – A + F=2[/tex].

A ideia de objetos homeomorfos explica porque alguns dos objetos que vocês examinaram na Atividade 6 têm a mesma característica de Euler-Poincaré: mesmo, a princípio, tendo formas geométricas bem diferentes eles podem ser deformados e transformados em um mesmo objeto.