|
P I P A
|
|
Sala 2
Uma pipa 3D
|
Tópicos
|
|
 |
Retornando das férias, nada como iniciar os estudos se divertindo…
|

I – Apresentação do Tema
Se pipas convencionais, com alguns centímetros e feitas apenas com papel, varetas e linha, já encantam quando colorem o céu, então o que dizer das pipas 3D?
Os enormes dragões chineses talvez sejam as pipas 3D mais conhecidas e, por incrível que pareça, apesar de todo aquele tamanho elas voam.
Não acreditam?
Então, vejam…
Sonzogni e seus Dragões
Mas não são apenas os dragões chineses que podem ser transformados em enormes objetos que voam. Em festivais de pipas 3D, conseguimos ver as mais variadas formas cruzando o céu.
Festivais de pipas
Cliquem na figura correspondente ao festival que vocês querem assistir.
Na janela que irá abrir, é só clicar na setinha e, depois de assistir a um vídeo, é só fechar a janela que se abriu.

|

|

|
| Wildwood, 2013 | Hammonasset, 2014 | Seal Beach, 2011 |
E se vocês acreditam que o céu é dos pássaros, concordamos com vocês!
Festival de pássaros pipas em Dieppe
Embora bonitas e, até, surpreendentes, não são essas as pipas 3D que iremos estudar. Estudaremos outro tipo com formas, digamos, mais matemáticas:
as Pipas Tetraédricas de Graham Bell.
Este será o tema desta Sala de Atividades e ele exigirá um pouco de visão espacial.
II – Até Graham Bell soltava pipas!
O nome Alexander Graham Bell lhes parece familiar?
Talvez a maioria das pessoas associem esse nome à invenção do telefone; não o telefone celular que utilizamos hoje em dia, mas aquele objeto que deu origem não somente ao celular, mas aos modernos sistemas de telecomunicações.
Embora Graham Bell seja conhecido e reconhecido por sua contribuição para o advento do telefone, há alguns indícios de que não foi ele quem inventou o objeto. Tanto que a patente número 174.465 concedida a Graham Bell em 7 de Março de 1876, pelo Escritório de Patentes dos Estados Unidos, foi revogada em 2002 em favor de Antonio Santi Giuseppe Meucci, pelo Congresso dos Estados Unidos.
Discórdias sobre a paternidade do telefone à parte, o que vai nos interessar é o envolvimento de Graham Bell com as pipas 3D.
 |
 |
| Alexander Graham Bell | Antonio Santi Giuseppe Meucci |
O desejo da humanidade de voar é tão antigo que talvez tenha nascido junto com o primeiro homem e, particularmente, Graham Bell envolveu-se com a discussão sobre a possibilidade de se construir máquinas voadoras aerodinamicamente estáveis.
Assim foi que, a partir de 1891, Graham Bell iniciou um novo projeto de estudo: a construção de uma estrutura com grande área de superfície e, ao mesmo tempo, leve, de modo que voasse e permitisse transportar um homem.
Seus estudos o levaram a combinar triângulos equiláteros e construir, a partir de 1902, pipas, utilizando tetraedros cobertos por tecido. As estruturas assim construídas poderiam ser pequenas, médias, grandes, ou muito grandes, dependendo do número de peças utilizadas; existem informações de que Graham Bell chegou a construir uma dessas estruturas com quase 4 mil tetraedros!
Estava, então, inventada a Pipa tetraédrica de Graham Bell: uma estrutura forte e rígida que voava…
Fotos da construção de uma torre de observação composta por células tetraédricas e inaugurada em agosto de 1907, assim como fotos de pipas tetraédricas construídas por Graham Bell, certamente darão uma ideia do objeto central dessa nossa discussão. Vejam as fotos e consultem as referências. Vale muito a pena!
 A torre de observação sendo construída. |
 Os triângulos utilizados na construção dos tetraedros. |
 Parte da torre de observação. |
 A torre de observação em uso. |
 Uma pipa tetraédrica construída na época de Graham Bell. |
 Graham Bell e sua esposa, Mabel Hubbard Bell |
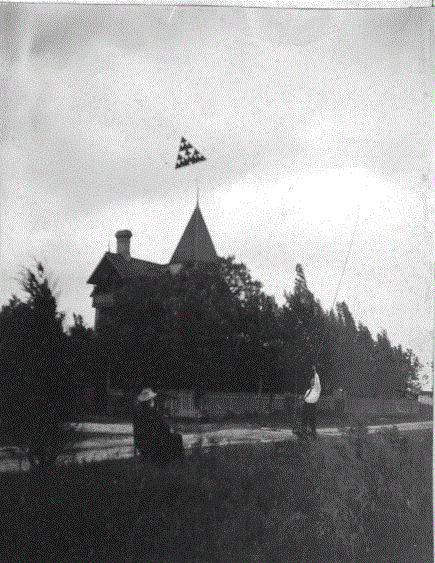 Uma pipa tetraédrica sendo empinada. |
 Outra pipa tetraédrica construída na época de Graham Bell. |
III – Pequenas pesquisas
Até aqui citamos alguns aspectos da vida de Graham Bell e a discórdia envolvendo a invenção do telefone, alertamos sobre a necessidade de um pouco de visão espacial para o entendimento das pipas tetraédricas e observamos que tetraedros de alguma forma são compostos por triângulos.
Agora está na hora de vocês começarem a trabalhar; assim, seria interessante vocês pesquisarem sobre a discórdia citada e recordarem alguns tópicos dessa área tão bonita da Matemática que é a geometria espacial.
Então, pesquisem os assuntos indicados abaixo para que vocês aprendam um pouco mais e possam aproveitar ainda mais toda a nossa discussão. Busquem informações na Internet, em livros e, mais uma vez, não dispensem a ajuda imprescindível de seus professores.
1) Quem foi Graham Bell?
2) Quem inventou o telefone?
3) Os sólidos platônicos.
4) O que são poliedros?
5) O que é uma pirâmide?
IV – As Pipas Tetraédricas de Graham Bell
O tema central desta Sala de Atividades é a pipa tetraédrica de Graham Bell, um objeto que, cerca de 120 anos depois de ter sido inventado, vocês terão a oportunidade de construir e de comprovar que ele, de fato, voa. Mas antes vale a pena entender que objeto é esse que vai ser construído.
O primeiro passo para isso é observar que uma pipa tetraédrica é uma estrutura formada por objetos que podem ser matematicamente definidos e, a partir dos quais, deriva o nome desse tipo de pipa: os tetraedros.
- se vocês sabem o que é uma pirâmide, podemos dizer que um tetraedro é uma pirâmide triangular, cujas faces são triângulos equiláteros;
- se vocês sabem o que é um poliedro, podemos dizer que um tetraedro é um poliedro regular formado por quatro triângulos equiláteros.
Características importantes de um tetraedro:
✓ Tem quatro faces.
✓ Cada face é um triângulo equilátero.
✓ Tem seis arestas.
✓ Tem quatro vértices.
✓ De cada vértice partem três arestas.
Vocês podem visualizar essas características utilizando o tetraedro do aplicativo disponibilizado a seguir.
- Cliquem no botão Spin para controlar o movimento da figura manualmente.
- Ao clicar no botão Drag, a figura volta a se movimentar automaticamente.
- Ao clicar no botão Explode, vemos separadamente os triângulos que definem a figura. Clicando novamente no botão, vemos o tetraedro.
Extraído de http://www.disfrutalasmatematicas.com/
Assim, o tetraedro é uma figura tridimensional que, quando “desmontada” e representada num plano, resulta em uma figura formada pela união de quatro triângulos equiláteros, necessariamente congruentes. Ao clicar no botão Explode do aplicativo é possível observar o movimento desses triângulos.
Esse processo de representação de um tetraedro no plano é um exemplo do que conhecemos na matemática como planificação. Vocês podem acompanhar a planificação de um tetraedro, no próximo vídeo.
Planificação de um tetraedro
Agora, o próximo passo é determinar como dispor os tetraedros, de modo a formar as estruturas que denominamos de pipas tetraédricas.
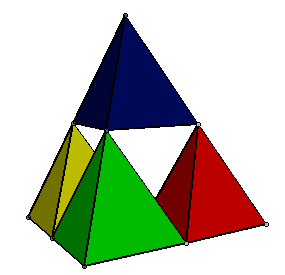
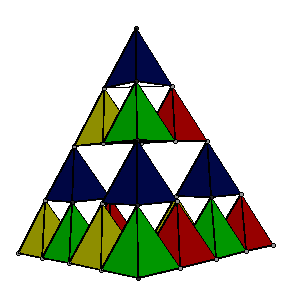
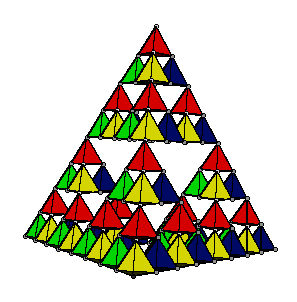
Observem atentamente cada estrutura da sequência de figuras abaixo e notem que:
- os tetraedros que formam cada pipa têm apenas duas de suas faces revestidas;
- a partir da segunda, cada pipa é construída a partir de quatro pipas do modelo anterior.
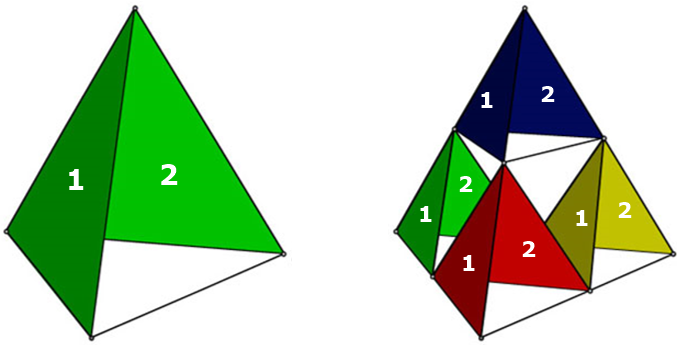
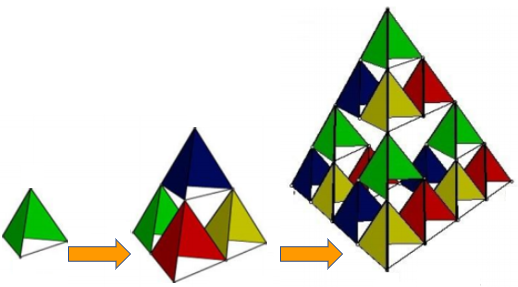
 |
 |
 |
 |
 |
| 1 célula | 4 células | 16 células | 64 células | 256 células |
Para vocês que conseguiram entender a estrutura das pipas tetraédricas de Graham Bell, só falta vê-las em ação.
Então, vamos lá, escolham uma das pipas – pequena, média ou grande – e cliquem na figura correspondente – primeira, segunda, terceira. Na janela que irá abrir, é só clicar na setinha e, depois de assistir a um vídeo, é só fechar a janela que se abriu.

|

|

|
V – Uma pipa do futuro
As Pipas Tetraédricas de Graham Bell inspiraram um casal de designers a construir a bela estrutura geométrica que pode ser apreciada nas próximas três imagens.



Os construtores são do País de Gales e criaram o modelo definitivo dessa forma a partir de uma impressora 3D. Segundo o Daily Mail, foram impressos conectores de nylon e 23 mil pedaços de materiais leves, como fibra de carbono. Foram necessários meses de trabalho para imprimir e construir a estrutura.
Vocês podem estar se perguntando:
O que essa forma geométrica faz em um tópico de pipas?
Aparentemente, ele é uma extravagante e bela forma geométrica, e nada mais. Mas, pasmem:
Ela voa e fica mais bela, ainda, no ar!
Se vocês não acreditam, vejam o vídeo abaixo. Aproveitem e observem outros detalhes da construção.
Little Shining Man
VI – Oficina para construção de pipas tetraédricas
Chegou a hora de vocês se divertirem!!!!
Que tal vocês organizarem pequenas oficinas em suas escolas para construir pipas tetraédricas de Graham Bell?
Pode parecer difícil; mas fiquem calmos, pois não é…
Vocês só precisarão ler com atenção as instruções que disponibilizaremos e pedir para que seus professores lhes ajudem na organização das oficinas e no acompanhamento da execução.
Então, mãos à obra…
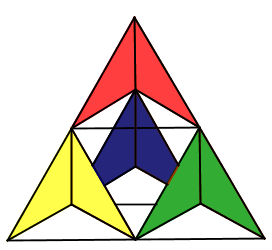
Instruções:
Clicando no link abaixo, vocês terão acesso a uma página contendo instruções, dicas e modelos para a construção de pipas tetraédricas com quatro células.
![]() Construção da pipa tetraédrica
Construção da pipa tetraédrica

Vídeos e fotos
Os melhores alunos de cada Programa de Iniciação Científica da OBMEP, PIC/OBMEP, participam de um encontro de uma semana, no qual assistem a palestras, oficinas, gincanas matemáticas e minicursos adequados aos seus respectivos níveis de escolaridade. No ano de 2014, esse encontro foi realizado em Florianópolis, Santa Catarina, e uma das atividades oferecidas aos participantes foi uma oficina para a construção de pipas tetraédricas de Graham Bell.
Disponibilizamos para vocês algumas fotos e um vídeo dessa oficina, que foi orientada pelo professor Humberto Bortolossi, docente da Universidade Federal Fluminense que, além de orientar, foi o idealizador da atividade.
VII – A matemática das pipas tetraédricas
O elemento matemático definidor de uma pipa tetraédrica é o poliedro conhecido por tetraedro, que por sua vez é definido a partir de quatro triângulos equiláteros. Nas atividades que se seguem, vamos explorar esses dois objetos matemáticos: o triângulo e o tetraedro.
Questão 9.1:
Quando nos referimos à planificação do tetraedro, afirmamos que
– “esse poliedro é uma figura tridimensional que, quando “desmontada” e representada num plano, resulta em uma figura formada pela união de quatro triângulos equiláteros, necessariamente congruentes.”
Justifiquem o porquê de os quatro triângulos serem necessariamente congruentes.
Questão 9.2: 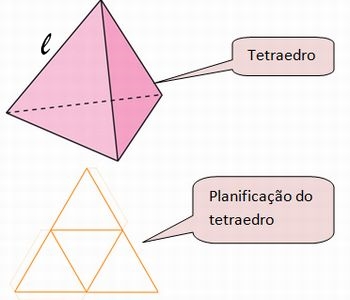 Suponha um tetraedro com arestas de comprimento l.
Suponha um tetraedro com arestas de comprimento l.
a) Qual é a área dos triângulos equiláteros que definem esse tetraedro?
b) Qual é a área total desse tetraedro?
c) Qual é o volume desse tetraedro?
Justifiquem.
A imagem abaixo mostra três pipas tetraédricas de Graham Bell e será utilizada como referência nas próximas questões.
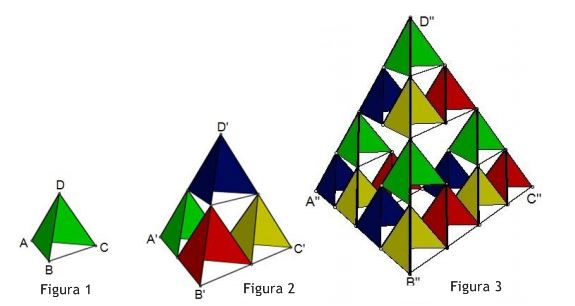
Observem que a estrutura da figura 2 é constituída por quatro réplicas da estrutura da figura 1 e a estrutura da figura 3 é formada por quatro réplicas da estrutura da figura 2.
Consideraremos que l é o comprimento dos canudos utilizados na construção das pipas das figuras 1, 2 e 3.
Questão 9.3:
a) Verifique que os triângulos [tex]ABC, \, A’B’C'[/tex] e [tex]A”B”C” [/tex] são semelhantes.
b) Qual é a razão entre as medidas dos segmentos [tex]AB, \, A’B'[/tex] e [tex]A”B”[/tex], tomados dois a dois?
c) Qual é a razão entre as áreas dos triângulos [tex]BCD, \, B’C’D'[/tex]e [tex]B”C”D”[/tex], tomados dois a dois?
d) Qual é a razão entre os volumes dos tetraedros [tex]ABCD, \, A’B’C’D'[/tex] e [tex]A”B”C”D”[/tex], tomados dois a dois?
Justifiquem.
Questão 9.4:
a) Quantos canudos são necessários para se construir a estrutura tetraédrica [tex] ABCD[/tex]?
b) Sabemos que a estrutura tetraédrica [tex]A’B’C’D'[/tex] é construída utilizando-se quatro cópias da estrutura tetraédrica [tex]ABCD[/tex]. Quantos canudos são necessários para se construir a estrutura tetraédrica [tex]A’B’C’D'[/tex]?
c) E quantos canudos são necessários para se construir a estrutura tetraédrica [tex]A”B”C”D”[/tex]?
d) Mais geralmente, se n é um número natural, quantos canudos são necessários para se construir uma estrutura tetraédrica que foi construída a partir de 2n cópias da estrutura tetraédrica [tex]ABCD[/tex]?
Justifiquem.
Questão 9.5:
Denominaremos de asa de uma pipa tetraédrica a toda face da pipa que está encapada. Assim as asas de uma pipa são as suas faces coloridas.
a) Qual é a área total das asas da estrutura tetraédrica [tex]ABC[/tex] (figura 1)?
b) Qual é a área total das asas da estrutura tetraédrica [tex]A’B’C’D'[/tex](figura 2)?
c) Qual é a área total das asas da estrutura tetraédrica [tex]A”B”C”D”[/tex] (figura 3)?
d) De maneira geral, qual é a área de uma estrutura tetraédrica que foi construída a partir de 2n cópias da estrutura tetraédrica [tex]ABCD[/tex]?
e) O que vocês podem concluir a partir dos cálculos efetuados?
Questão 9.6:
Suponha que cada canudo tenha peso P e que os pesos das asas e das linhas sejam desprezíveis em comparação com o peso do canudo.
a) Calcule a razão entre o peso e a área total das asas da estrutura tetraédrica [tex]ABCD[/tex] (figura 1).
b) Calcule a razão entre o peso e a área total das asas da estrutura tetraédrica [tex]A’B’C’D'[/tex] (figura 2).
c) Calcule a razão entre o peso e a área total das asas da estrutura tetraédrica [tex]A”B”C”D”[/tex] (figura 3).
d) De maneira geral, calcule a razão entre o peso e a área total das asas da estrutura tetraédrica que foi construída a partir de 2n cópias da estrutura tetraédrica [tex]ABCD[/tex].
e) O que vocês podem concluir a partir dos cálculos efetuados?
VIII – Uma investigação
Já comentamos que a pipa tetraédrica de Alexander Graham Bell foi construída a partir do envolvimento de seu criador na discussão sobre a possibilidade de se construir máquinas voadoras, mas essa não era uma preocupação apenas de Graham Bell.
O início do século XX foi cientificamente pautado pela preocupação se seria possível ou não a construção de grandes aparatos voadores estáveis o suficiente para levar um homem aos céus e trazê-lo de volta em absoluta segurança.
Participe dessa discussão e entenda em que contexto nasceram as pipas tetraédricas e como a matemática ajudou Graham Bell.
IX – Um céu do início do século XX
Que tal vocês aproveitarem as pipas tetraédricas que construíram e organizarem um festival de pipas tetraédricas e com isso reproduzirem o céu de um dia do início do século XX?
A primeira coisa a fazer, antes de colocar as pipas construídas no ar, é convidar um bombeiro ou um policial para fazer palestra sobre os cuidados necessários ao brincar de pipa.
Depois, aproveitando a presença do bombeiro, ou do policial, reúnam-se com seus professores e organizem os passos iniciais do festival:
- Escolham o local.
- Decidam se vai acontecer apenas uma revoada de pipas ou um concurso de pipas.
- Definam a Comissão Organizadora do Evento.
Definida a Comissão, esta ficará responsável pela organização do Festival: datas, autorizações, convidados, divulgação, entre outros afazeres.
Se a opção for promover um concurso de pipas, será essencial providenciar um regulamento, definindo:
- Categorias, por exemplo:
– a pipa tetraédrica mais bonita;
– a maior pipa tetraédrica;
– a pipa tetraédrica que voa mais alto.
- Tipos de participação, por exemplo:
– individual; por equipe; por sala de aula; por família.
- Regras
- Critérios de pontuação
- Premiação
- Jurados
- Inscrições (Poderá ser arrecadado, como inscrição, um quilo de alimento não perecível. Os alimentos arrecadados poderão ser entregues a alguma instituição de caridade.)
X – Encerramento do tema
A observação do voo dos pássaros e a forma com que eles se sustentam no ar pela força do movimento de balanço de suas asas ainda hoje ocupa a cabeça e os sonhos de muitas pessoas. Esse é mais um sonho que, ao longo da história, levou diversos pensadores e cientistas a desenvolverem projetos de máquinas com base nessa forma de voar.
O filósofo e monge inglês Roger Bacon (1219-1292) já no final do século XIII afirmou que as pessoas poderiam construir máquinas que lhes permitissem voar sendo sustentadas pelo ar, assim como um navio é sustentado pela água. Por volta de 1490, essa afirmação foi transformada em projeto pelo artista, inventor e cientista italiano Leonardo da Vinci (1452-1519).
A máquina projetada por da Vinci, o ornitóptero (do grego, ornithos (ave) + pteron (asa)), tinha como objetivo ser capaz de fazer o homem voar batendo as asas, assim como fazem os pássaros.
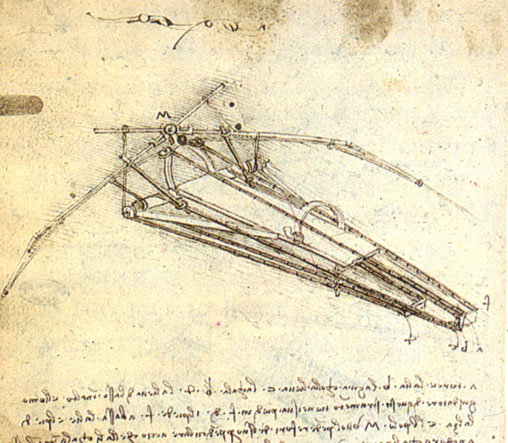
Ornitóptero de “da Vinci”
Leonardo da Vinci nunca testou sua máquina, mas seu sonho parece que está ganhando vida: engenheiros da FESTO (empresa alemã que desenvolve maquinário para automação industrial) desenvolveram um protótipo capaz de imitar, muito de perto, o voo dos pássaros. O robô se chama SmartBird e é capaz de voar simplesmente batendo as suas asas mecânicas.
É com o voo dessa pipa 3D sem linhas e varetas que encerramos a Sala de Atividades
O inacreditável pássaro robô SmartBird

Para ver uma rápida explicação sobre o mecanismo do SmartBird,
por um de seus criadores, clique aqui.



➨ A pipa tetraédrica de Graham Bell: abordagem em sala de aula como elemento motivador da aprendizagem (Site acessado em 20/11/19)
➨ Cometas tradicionales (Texto acessado em 20/11/19)
➨ Portal do Professor (Site acessado em 20/11/19)
➨ Um estudo sobre poliedros e atividades para o ensino de matemática (Site acessado em 20/11/19)
Equipe COM – OBMEP
Junho de 2015.
➨ ABC Design (Site acessado em 02/03/15)
➨ UFF – Conteúdo Digital (Site acessado em 20/11/19)
➨ Daily Mail (Site acessado em 20/11/19)
➨Licenças sob Domínio público via Wikimedia Commons
➨ Portal do Professor (Site acessado em 20/11/19)
➨Vimeo (Site acessado em 20/11/19)
➨YouTube (Site acessado em 20/11/19)

