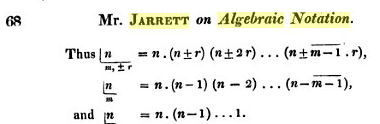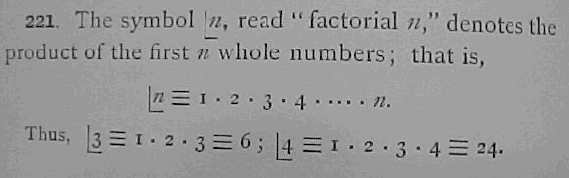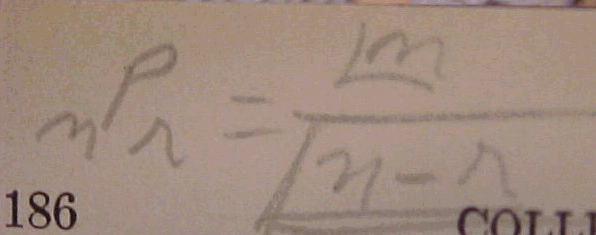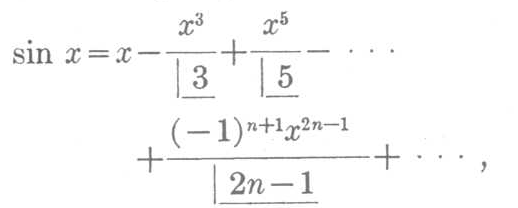|
Vamos apresentar mais formalmente dois conceitos importantes que aparecem naturalmente quando lidamos com o Princípio Fundamental da Contagem: fatorial e permutação simples. |
De quantas maneiras os cinco membros de um Clube Olímpico de Matemática podem se organizar em uma sala de computação com cinco computadores?
No caso do problema formulado, há 5 possibilidades para escolhermos a pessoa que utilizará o primeiro computador. Escolhida tal pessoa, há 4 possibilidades para aquela que ocupará o segundo computador.
Seguindo esse raciocínio, é muito simples perceber que, utilizando o PFC, a resposta ao problema será:
5 ⋅ 4 ⋅ 3⋅ 2 ⋅ 1 = 120.
Imagine, porém, que o problema inicial se referisse a 100 funcionários do Call Center de uma importante empresa que fossem fazer um treinamento em uma gigantesca sala de computação, com 100 computadores. Será que, para registrarmos a solução, precisaríamos escrever o correspondente produto com cem fatores???
Com certeza não precisaríamos escrever todos os cem fatores e nem mesmo expressões com uso de reticências, como, por exemplo, 100 ⋅ 99 ⋅ 98 ⋅ . . . ⋅ 2 ⋅ 1. Explicitar produtos como esse toda vez que eles aparecerem é algo desnecessário, já que o matemático francês Christian Kramp (Conheça um pouco do trabalho desse matemático aqui.) decidiu adotar uma notação muito simples para produtos desse tipo: ele decidiu representar o fatorial do número n por n! (leia n fatorial).
– Elegante, não é?
Porém, esta notação não foi a única utilizada para representar o fatorial de um número natural. Para conhecer um pouco dessa história, clique no botão abaixo.
Agora que já viajamos um pouco pela história do fatorial, vamos conferir alguns exemplos? Observe:
4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24;
10! = 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 3628800
n! = n ⋅ (n – 1) ⋅ (n – 2) ⋅ … ⋅ 3 ⋅ 2 ⋅ 1.
De uma maneira mais formal, o fatorial de um número natural [tex]n[/tex] é o número denotado por [tex]n![/tex] e definido da seguinte forma:
• [tex]n!=1[/tex], se [tex]n=0[/tex];
• [tex]n!=n \cdot (n-1)![/tex], se [tex]n\gt 0[/tex].
A atenção e o cuidado na hora de trabalhar com fatoriais é muito importante. A soma[tex] \, a! + b! \, [/tex] ou o produto [tex] \, a! \cdot b! \, [/tex] , por exemplo, não são equivalentes a [tex] \, (a + b)! \, [/tex] ou a [tex] \, (a \cdot b)! \, [/tex](tente entender o porquê!).
Uma interessante propriedade dos fatoriais é a de que, se [tex]a[/tex] e [tex]b[/tex] forem números naturais, com [tex]a\gt b[/tex], então
[tex] \qquad\qquad \dfrac{a!}{b!} = a(a-1)(a-2)\cdot \, \cdots \, \cdot(b+1)[/tex]
ou, de forma equivalente,
[tex]\qquad\qquad a!=a(a-1)(a-2)\cdot \, \cdots \, \cdot(b+1)\cdot b! [/tex].
Que tal tentar provar essas igualdades?
Elas facilitam bastante cálculos que envolvam fatoriais. De acordo com elas, nós temos, por exemplo, [tex]\dfrac{10!}{9!} = 10[/tex] e [tex]\dfrac{50!}{47!} = 50\cdot 49\cdot 48 = 117600[/tex]. Por que isso ocorre?
Podemos utilizar o PFC e resolver o problema geral de uma permutação simples com n objetos distintos: calcular a quantidade de maneiras de dispormos n diferentes objetos em fila. Para tanto, vamos realizar um raciocínio semelhante ao realizado no início do texto: calcular o número de maneiras que podemos escolher o objeto que ocupará o primeiro lugar da fila, depois o segundo lugar, depois o terceiro, até esgotar as [tex]n[/tex] posições da fila.
| n escolhas | (n-1) escolhas | … | 2 escolhas | 1 escolha | ||||
| 1º lugar da fila | 2º lugar da fila | (n-1)º lugar da fila | nº lugar da fila |
A resposta será [tex]n![/tex] , não será?
Portanto, o número de permutações simples de [tex]n[/tex] objetos em fila fica definido pela igualdade [tex] P_n=n![/tex].
Útil e fácil!
Formalmente:
Permutações simples são definidas como maneiras de organizarmos [tex]n[/tex] objetos distintos em uma fila. O número total de permutações simples é denotado por [tex]P_n[/tex] e é verificada a igualdade [tex]P_n=n![/tex]
Pequenas atividades:
1. Quantos algarismos você acha que o número 14! possui?
2. Em quantas ordens diferentes você pode pedir o autógrafo dos 11 jogadores titulares de um time de futebol?
A maquineta disponibilizada abaixo poderá ajudar nos cálculos da segunda atividade e também na hora de conferir o palpite da primeira. Além disso, você poderá utilizá-la para calcular o fatorial de qualquer número natural menor que 21.
É importante lembrar que o conceito de permutação simples é constantemente ligado ao de fatorial, mas a recíproca nem sempre é verdadeira! Há outras áreas da matemática que utilizam o fatorial; não somente a Contagem e a Combinatória.
MAQUINETA 1
A maquineta funciona adequadamente no Excel.
☞ MAQUINETA 2 – Utilize esta Maquineta para comparar os valores [tex]a! + b! \, [/tex] e [tex] \, (a + b)! [/tex].
MAQUINETA 2
A maquineta funciona adequadamente no Excel.
☞ MAQUINETA 3 – Utilize esta Maquineta para comparar os valores [tex]a! \cdot b! \, [/tex] e [tex] \, (a \cdot b)! [/tex].
MAQUINETA 3
A maquineta funciona adequadamente no Excel.
Observação: Ao abrir o arquivo de uma Maquineta, observe se a planilha está no Modo de Exibição Protegido.
Em caso positivo, habilite a Edição antes de usar a Maquineta.
– Francimar de Brito Vieira
– Noemi Zeraick Monteiro
– Sonia Regina Di Giacomo
◆ Equipe COM – OBMEP
Voltar para a Sala de Estudos sobre o PFC
|
Agora eu posso concordar… |
 |
 |
Que bom que está gostando dos temas. |
|
Vamos lá! |
 |
Referências, acessadas em 04/08/18:
http://www.pballew.net/arithme2.html;
http://www-history.mcs.st-and.ac.uk/Biographies/Kramp.html.