|
Apresentaremos aqui algumas definições e propriedades básicas relativas ao estudo de probabilidade para ajudá-los com os problemas e as atividades do nosso Blog.
|
Probabilidade e eventos
Eventos
A Teoria das Probabilidades é o ramo da Matemática que fornece ferramentas para modelarmos os chamados fenômenos ou experimentos aleatórios, isto é, aquelas ações em que o "acaso" representa um papel preponderante e não podemos prever com certeza o que vai acontecer. São exemplos de experimentos aleatórios:
(2) Escolher uma peça de um lote de fabricação e verificar se a mesma tem ou não defeito.
(3) A cobrança de um pênalti por um jogador de futebol.
(4) O lançamento de uma moeda e a verificação se, depois da queda, a face voltada para cima é cara ou coroa.
(5) A retirada de uma bola de uma urna com [tex]50[/tex] bolas numeradas de [tex]1[/tex] a [tex]50[/tex] e observação de seu número.
(6) Verificar o tipo sanguíneo de um habitante de uma cidade escolhido ao acaso.
(7) Retirar uma carta de um baralho completo e verificar o seu naipe.
Mesmo apresentando resultados imprevisíveis se repetidos várias vezes em processos semelhantes, podemos quantificar a chance que cada resultado possível tem de ocorrer em fenômenos aleatórios utilizando ferramentas da Teoria das Probabilidades. Para facilitar a apresentação dessas ferramentas, é usual denominar o conjunto de todos os possíveis resultados de um experimento aleatório de espaço amostral do experimento e de eventos os possíveis resultados de um experimento.
Cada elemento de um espaço amostral é denominado ponto amostral.
► Evento: qualquer subconjunto do espaço amostral. Os eventos geralmente são indicados por letras maiúsculas do nosso alfabeto, indexadas ou não; e, na prática, dizemos que um evento E ocorre se, quando realizado o experimento, obtém-se um resultado que pertence a E.
Um primeiro passo no estudo de um experimento aleatório é compreendermos os resultados possíveis de se obter com a realização desse experimento, ou seja, antes de mais nada, é necessário conhecer e entender bem o espaço amostral do experimento.
► Para os experimentos exemplificados acima, observe que os respectivos espaços amostrais são os seguintes:
(2) [tex]\Omega_2 = \{[/tex]peça defeituosa , peça sem defeitos[tex]\}[/tex].
(3) [tex]\Omega_3 = \{[/tex]pênalti convertido , pênalti desperdiçado[tex]\}[/tex] ou
[tex]\quad \;\Omega_3 = \{[/tex]pênalti convertido , defesa do goleiro , bola chutada para fora[tex]\}[/tex],
dependendo do que desejamos analisar.
(4) [tex]\Omega_4=\{[/tex]cara , coroa[tex]\}[/tex].
(5) [tex]\Omega_5=\{1,2,3,4,\cdots,49,50\}[/tex].
(6) [tex]\Omega_6=\{A, B, AB, O\}[/tex].
(7) [tex]\Omega_7=\{[/tex]ouros, copas, paus, espadas[tex]\}[/tex].
► Para esses experimentos, podemos, por exemplo, definir respectivamente os seguintes eventos:
(2) [tex]E_2:[/tex] A peça escolhida é defeituosa. Neste caso, [tex]E_2=\{[/tex]peça defeituosa [tex]\}\subset \Omega_2[/tex].
(3) [tex]E_3:[/tex] O jogador fez o gol. Neste caso, [tex]E_3= \{[/tex]pênalti convertido[tex]\}\subset \Omega_3[/tex].
(4) [tex]E_4:[/tex] Obter cara. Neste caso, [tex]E_4=\{[/tex]cara[tex]\}\subset \Omega_4[/tex].
(5) [tex]E_5:[/tex] Retirar uma bola com numeração acima de [tex]45[/tex]. Neste caso, [tex]E_5=\{46,47,48,49,50\}\subset \Omega_5[/tex].
(6) [tex]E_6:[/tex] O tipo sanguíneo do habitante é [tex]AB[/tex]. Neste caso, [tex]E_6=\{AB\}\subset \Omega_6[/tex].
(7) [tex]E_7:[/tex] O naipe da carta é paus. Neste caso, [tex]E_7=\{[/tex]paus[tex]\}\subset \Omega_7[/tex].
Tipos especiais de eventos
► Há eventos que sempre ocorrem e por isso são chamados de eventos certos. Já os que nunca ocorrem são chamados de eventos impossíveis.
Lançar um dado, cujas faces estão numeradas de [tex]1[/tex] a [tex]6[/tex], e "obter um número menor do que oito" é um evento certo; mas "obter um número maior do que dez" é um evento impossível.
► Dentro de um mesmo espaço amostral, quando a ocorrência de um evento impossibilita a ocorrência de outro evento dizemos que os eventos são mutuamente excludentes ou disjuntos.
No lançamento de um dado com as faces numeradas de [tex]1[/tex] a [tex]6[/tex], por exemplo, os eventos "obter um valor maior do que quatro" e "obter um valor menor do que 2" são mutuamente excludentes, já que os dois não podem ocorrer simultaneamente.
► Os eventos que possuem apenas um resultado do experimento são chamados de eventos elementares ou eventos simples; esses eventos são os subconjuntos unitários do espaço amostral. Assim, cada evento elementar é formado por um único ponto amostral.
Os eventos [tex]E_2[/tex], [tex]E_3[/tex], [tex]E_4[/tex], [tex]E_6[/tex] e [tex]E_7[/tex] dos nossos exemplos de experimentos são todos elementares. No lançamento de um dado, cujas faces estão numeradas de [tex]1[/tex] a [tex]6[/tex], temos seis eventos elementares: [tex]\{1\}[/tex], [tex]\{2\}[/tex], [tex]\{3\}[/tex], [tex]\{4\}[/tex], [tex]\{5\}[/tex] e [tex]\{6\}[/tex]. No Sorteio da Mega-Sena, cada cartão com seis números que pode ser apostado é um exemplo de um evento elementar.
Observe que, como os eventos são conjuntos, podemos definir operações entre eles.
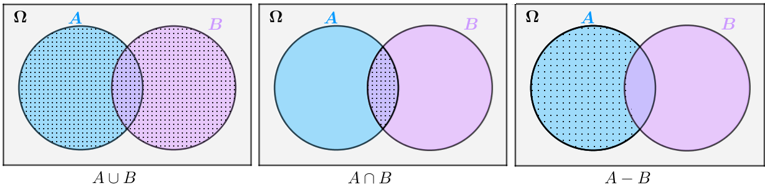
Dessa forma, dados dois eventos podemos utilizar operações entre conjuntos de modo a criar novos eventos, como mostramos abaixo.
Composição de eventos
Sejam [tex]A[/tex] e [tex]B[/tex] eventos de um mesmo experimento aleatório.
► O conjunto [tex]A \cup B\;[/tex] indica um evento que ocorre se e somente se pelo menos um dos dois eventos, [tex]A[/tex] ou [tex]B[/tex], ocorre.
► O conjunto [tex]A \cap B\;[/tex] indica um evento que ocorre se e somente se os dois eventos, [tex]A[/tex] e [tex]B[/tex], ocorrem simultaneamente.
– Usando essa simbologia, podemos dizer que os eventos [tex]A[/tex] e [tex]B[/tex] são mutuamente excludentes quando [tex]A \cap B=\emptyset [/tex].
► O conjunto [tex]A-B\;[/tex] indica um evento que ocorre se e somente se [tex]A[/tex] ocorre, mas [tex]B[/tex] não ocorre.
► O evento complementar de um evento [tex]A[/tex], que indicamos por [tex]\overline{A}[/tex] ou [tex]A^C[/tex], é o conjunto formado por todos os resultados do experimento que não pertencem a [tex]A[/tex]. Assim, [tex]\overline{A}[/tex] ocorre se e somente se [tex]A[/tex] não ocorre.
Se [tex]A_1,A_2,\cdots,A_n[/tex] são eventos de um mesmo experimento aleatório, podemos generalizar as duas combinações iniciais de eventos.
► A união [tex]A_1\cup A_2\cup \cdots \cup A_n\;[/tex], que pode ser simbolizada por [tex] {\textstyle \bigcup\limits_{i=1}^n} A_i[/tex], indica um evento que ocorre quando pelo menos um dos eventos [tex]A_i[/tex] ocorrer.
► A interseção [tex]A_1\cap A_2\cap \cdots \cap A_n\;[/tex], que pode ser simbolizada por [tex] {\textstyle \bigcap\limits_{i=1}^n} A_i[/tex], indica um evento que ocorre quando todos os eventos [tex]A_i[/tex] ocorrerem.
Para ver alguns exemplos de eventos definidos a partir de outros eventos, clique no botão abaixo.
A chance de um evento ocorrer
Em experimentos aleatórios, embora não saibamos que evento irá ocorrer, podemos prever que alguns eventos têm mais chances de ocorrer do que outros. Por exemplo em um lançamento de um dado não viciado, cujas faces estão numeradas de [tex]1[/tex] a [tex]6[/tex], e a verificação da numeração da face voltada para cima, se compararmos as chances de ocorrerem os seguintes eventos:
[tex]\qquad D_1:[/tex] obter um número menor do que seis;
[tex]\qquad D_2:[/tex] obter o número seis;
podemos concluir que, embora não seja impossível que [tex]D_2[/tex] ocorra, a chance de ocorrência do evento [tex]D_1[/tex] é maior.
Vamos então olhar os experimentos aleatórios sob um ponto de vista quantitativo e tentar associar a cada evento de um experimento aleatório números que nos deem uma indicação da chance de ocorrência desse evento quando o experimento em questão for realizado repetidas vezes, nas mesmas condições. Lembramos que nesta nossa conversa trataremos apenas de experimentos aleatórios cujos espaços amostrais são conjuntos finitos, como os mostrados nos nossos exemplos anteriores.
Frequência Relativa
Uma maneira, digamos, prática de atribuir a um evento [tex]E[/tex] um número que avalie as chances de ocorrência desse evento é determinar o que definiremos como a frequência relativa de [tex]E.[/tex]
Suponhamos que esse experimento seja repetido [tex]N[/tex] vezes, nas mesmas condições, e nestas o evento [tex]E[/tex] ocorra exatamente [tex]m[/tex] vezes, [tex]m\leqslant N[/tex].
Então, a frequência relativa de vezes que o evento [tex]E[/tex] ocorreu, ou simplesmente a frequência relativa de [tex]E[/tex], é denotada por [tex]f(E)[/tex] e assim definida:
[tex]\boxed{\textcolor{#8b4513}{f(E)=\dfrac{\,m\,}{N}}}\,.[/tex]
Observação importante: Como [tex]0 \leqslant m\leqslant N[/tex], então [tex]\boxed{0 \leqslant f(E) \leqslant 1}\,.[/tex]
Assim, quando for necessário utilizar porcentagem para expressar uma frequência relativa, lembre-se de multiplicar o resultado da divisão [tex]\dfrac{\,m\,}{N}[/tex] por [tex]100[/tex], ou de utilizar uma regra de três.
A frequência relativa de um evento pode sempre ser calculada, mas para que a frequência relativa de um evento [tex]E[/tex] mostre, de fato, a chance de [tex]E[/tex] ocorrer, o experimento aleatório ao qual o evento está associado deve ser repetido muitas vezes. Isso porque somente se o experimento se repetir um número muito grande de vezes é que a frequência relativa de um evento se estabilizará próxima de algum número.
Dessa forma, não é porque você fez quatro lançamentos de uma moeda e obteve três caras e apenas uma coroa que, em um lançamento qualquer, a chance de se obter cara é [tex]\dfrac{3}{4}[/tex] ([tex]75\%[/tex]) e a chance de se obter coroa é [tex]\dfrac{1}{4}[/tex] ([tex]25\%[/tex]).
Vimos que a experiência de se lançar uma moeda honesta e verificar a face voltada para cima, depois da queda, tem como espaço amostral o conjunto [tex]\{[/tex]cara , coroa[tex]\}[/tex]. Intuitivamente, espera-se que a frequência relativa aos eventos "obter cara" e "obter coroa" seja de [tex]50\%[/tex] cada, ou seja, metade dos lançamentos obtemos cara e a outra metade, coroa. Observem:
► Pearson jogou uma moeda [tex]24\,000[/tex] vezes e obteve [tex]12\,012[/tex] caras; o que resulta em uma frequência relativa de [tex]\dfrac{12012}{24000}= 0,5005[/tex], ou seja, [tex]50,05\%[/tex] de caras.
► Kerrich jogou uma moeda [tex]10\,000[/tex] vezes e obteve [tex]5\,067[/tex] caras; o que resulta em uma frequência relativa de [tex]\dfrac{5067}{10000}= 0,5067[/tex], ou seja, [tex]50,67\%[/tex] de caras.
Probabilidade Clássica
Para não dependermos exclusivamente da repetição de um experimento com a finalidade de obtermos a chance de ocorrência de um evento, vamos apresentar um procedimento teórico cuja utilização depende de alguns cuidados. O mais importante é observar com atenção o tipo de espaço amostral no qual esse procedimento pode ser utilizado.
A cada evento elementar [tex]\{a_i\}[/tex] vamos associar um número real [tex]p_i[/tex], denominado probabilidade do evento [tex]\{a_i\}[/tex] ou probabilidade de ocorrência do ponto amostral [tex]a_i\,[/tex], que satisfaz as seguintes condições:
[tex]\qquad \textcolor{#8b4513}{\textbf{(i)}}[/tex] [tex]0 \leqslant p_i \leqslant 1\,,\;\forall i\in \{1,2,\cdots,k\}[/tex].
[tex]\qquad \textcolor{#8b4513}{\textbf{(ii)}}[/tex] [tex]p_1+p_2+\cdots+p_k=1\,[/tex].
Particularmente, se [tex]p_1=p_2=\cdots=p_k[/tex], diremos que o espaço [tex]\Omega[/tex] é equiprovável. Portanto, espaços equiprováveis são aqueles cujos pontos amostrais têm a mesma probabilidade de ocorrer. Nesse caso, se [tex]p[/tex] for essa probabilidade, segue de [tex]\textcolor{#8b4513}{\textbf{(ii)}}[/tex] que:
[tex]\qquad \underbrace{p+p+\cdots+p}_{k\text{ vezes}}=1\\
\qquad k\cdot p=1\\
\qquad p=\dfrac{1}{k}\,.[/tex]
Para espaços amostrais equiprováveis, podemos definir números que traduzam nossa expectativa de ocorrência de seus eventos. De agora em diante, o número que indica a chance de ocorrência de um evento [tex]E[/tex] será denominado probabilidade de [tex]E[/tex] e será denotado por [tex]P(E)\,.[/tex]
Definição clássica de probabilidade
Suponha um experimento aleatório cujo espaço amostral é finito e equiprovável. Se [tex]E[/tex] é um evento qualquer do espaço amostral [tex]\Omega[/tex] desse experimento aleatório, a probabilidade do evento [tex]E[/tex] ocorrer, ou simplesmente a probabilidade do evento [tex]E[/tex], é definida como a razão entre o número de elementos de [tex]E[/tex] e número de elementos de [tex] \Omega[/tex]. Em símbolos,
[tex] P(E)=\dfrac{n(E)}{n(\Omega)}[/tex],
sendo [tex]n(E)[/tex] o número de elementos do evento e [tex]n(\Omega)[/tex] o número de elementos do espaço amostral.
Informalmente, podemos dizer que a probabilidade de um evento é o número de casos favoráveis dividido pelo número de casos possíveis:

Observação importante: Como [tex]E \subset \Omega[/tex], então [tex]n(E) \leqslant n(\Omega)[/tex]. Assim, [tex]\boxed{0 \leqslant P(E) \leqslant 1}\,.[/tex]
Assim, quando for necessário utilizar porcentagem para expressar uma probabilidade, lembre-se de multiplicar o resultado da divisão [tex]\dfrac{n(E)}{n(\Omega)}[/tex] por [tex]100[/tex] ou de utilizar uma regra de três.
Vejamos alguns cálculos utilizando, mais uma vez, os nossos exemplos.
► No caso do lançamento de um dado, exemplo (1), quando queremos saber qual a chance de o resultado obtido ser par, estamos buscando estabelecer qual a probabilidade do evento [tex]E_1=\{2 , 4 , 6\}[/tex] ocorrer:
[tex]\qquad \qquad P(E_1)=\dfrac{n(E_1)}{n(\Omega_1)}=\dfrac{3}{6}=\dfrac{1}{2}=0,5.[/tex]
Percentualmente, [tex]P(E_1)=50\%.[/tex]
► Retirada uma carta de um baralho completo, exemplo (7), a probabilidade de o seu naipe ser paus é dada por:
[tex]\qquad \qquad P(E_7)=\dfrac{n(E_7)}{n(\Omega_7)}=\dfrac{1}{4}=0,25.[/tex]
Percentualmente, [tex]P(E_7)=25\%.[/tex]
► A probabilidade de se retirar uma bola com numeração acima de [tex]45[/tex] de uma urna com [tex]50[/tex] bolas numeradas de [tex]1[/tex] a [tex]50[/tex], exemplo (5), é:
[tex]\qquad \qquad P(E_5)=\dfrac{n(E_5)}{n(\Omega_5)}=\dfrac{5}{50}=\dfrac{1}{10}=0,1.[/tex]
Percentualmente, [tex]P(E_5)=10\%.[/tex]
As primeiras considerações formais sobre esta forma de calcular a chance de ocorrência de eventos provêm do século XVII como consequência do estudo dos jogos de azar. O assunto aparece especificamente em trocas de correspondências entre os matemáticos Pierre de Fermat (1601 – 1665) e Blaise Pascal (1623 – 1662) e nos estudos do matemático Christiaan Huygens (1629-1695). Mas foi o o matemático, físico e astrônomo francês Pierre Simon Laplace (1749-1827) quem primeiro apresentou formalmente a probabilidade como uma razão entre o número de casos favoráveis e o número de casos possíveis.
Probabilidades
De maneira geral, a frequência relativa utilizada para medir a chance de ocorrência de um evento é denominada probabilidade frequencial. Assim, apresentamos a você duas das várias maneiras de se definir probabilidade:
► o modelo frequencial ou frequentista, que utiliza a frequência relativa de um evento para medir a sua chance de ocorrer;
► o modelo equiprobabilístico, que utiliza a definição clássica de probabilidade de um evento para medir a sua chance de ocorrer.
Um terceiro modelo para o estudo de probabilidade é o modelo axiomático, que não será tratado aqui. O modelo axiomático generaliza os vários modelos de probabilidade.
De qualquer forma, a probabilidade é o número que associamos a um evento com a finalidade de estimar a chance de ele acontecer como resultado de um experimento aleatório. Bom, nesse momento da nossa conversa você poderá estar com a seguinte dúvida:
Probabilidade mede a chance de um evento acontecer e temos duas definições de probabilidade.
Então, qual é a chance: o número dado pela frequência relativa ou o dado pela probabilidade clássica?
"Frequência relativa" X "Probabilidade Clássica"
Quando introduzimos a noção de frequência relativa, observamos que:
A frequência relativa de um evento pode sempre ser calculada, mas para que a frequência relativa de um evento [tex]E[/tex] mostre, de fato, a chance de [tex]E[/tex] ocorrer, o experimento aleatório ao qual o evento está associado deve ser repetido muitas vezes. Isso porque somente se o experimento se repetir um número muito grande de vezes é que a frequência relativa de um evento se estabilizará próxima de algum número.
Pois bem, em espaços amostrais finitos e equiprováveis, o número ao qual a frequência relativa de um evento se estabilizará próxima é a chamada probabilidade clássica: a razão entre o número de elementos do evento e o número de elementos do espaço amostral.
Matematicamente falando, "a estimativa da probabilidade de um evento [tex]E[/tex] por frequência relativa é cada vez mais próxima da chamada probabilidade clássica do evento [tex]E[/tex], quando o número [tex]N[/tex] de repetições do experimento tender ao infinito".
Essa aproximação provoca uma observação interessante, que inclusive serve para renomear a frequência relativa e a probabilidade clássica, já que, não raramente, a probabilidade clássica e a frequência relativa são, respectivamente, denominadas de probabilidade "a priori" e probabilidade "a posteriori" uma vez que a primeira é obtida antes até de um experimento acontecer e a segunda é obtida após várias realizações do experimento.
No que se segue, o número que indica a chance de ocorrência de um evento [tex]E[/tex] será tratado como probabilidade de [tex]E[/tex] e será denotado por [tex]P(E)\,[/tex], independentemente de esse número ser uma probabilidade frequencial ou uma probabilidade clássica.
Existem várias propriedades que ajudam bastante na hora de resolvermos alguns problemas de probabilidade. Vamos apresentar, a seguir, algumas delas. (Aqui não nos preocuparemos com as demonstrações; isso será feito em outra Sala!)
Algumas propriedades das probabilidades
Sejam [tex]A[/tex] e [tex]B[/tex] eventos de um mesmo experimento aleatório cujo espaço amostral seja finito e os eventos elementares sejam igualmente "prováveis".
Então:
► [tex]P(\emptyset) = 0[/tex].
► [tex]P(\overline{A}) = 1 – P(A)[/tex]. (Essa é a probabilidade do evento [tex]A[/tex] não ocorrer.)
► Se [tex]A \subset B[/tex], então [tex]P(A) = P(B) – P(B – A)[/tex].
► Se [tex]A \subset B[/tex], então [tex]P(A) \leqslant P(B)[/tex].
► [tex]P(A \cup B) = P(A) + P(B) – P(A \cap B)[/tex].
► Se [tex]A[/tex] e [tex]B[/tex] forem mutuamente excludentes, ou disjuntos, então [tex]P\left(A\cup B\right)=P\left(A\right)+P\left( B\right)[/tex].
Vamos considerar o exemplo inicial (5) para fazermos algumas aplicações dessas propriedades.
Para ver essas aplicações, clique no botão abaixo e, após a leitura, não se esqueça de ocultar o material, para não sobrecarregar o visual!
Precisa de mais exemplos?
Então, clique no botão abaixo e lembre-se de que, antes de sair aplicando propriedades, você tem que se preocupar com a definição correta do espaço amostral do experimento que você está analisando.
Se o espaço amostral for equiprovável, você também terá que contar os casos prováveis e os casos possíveis; para isso, Diagramas de Venn e o Princípio Fundamental da Contagem podem ajudar!
Finalizando, é sempre bom lembrar que uma mesma palavra pode ter vários significados. Particularmente nesta Sala utilizamos a palavra chance com o significado que encontramos em um dicionário da língua portuguesa, ou seja, como a "possibilidade de algo acontecer", como podemos ver, por exemplo, clicando AQUI.
Fazemos esta observação, pois em Estatística a palavra chance pode ser definida como a razão entre probabilidade de um evento ocorrer e a probabilidade do evento não ocorrer, isto é, [tex] \dfrac{p} {1-p}[/tex], com [tex]p[/tex] sendo a probabilidade de o evento em questão ocorrer. Assim, poderíamos dizer que, neste caso, a chance seria a razão do esperado pelo inesperado!
Mas isso é assunto para outra Sala….
Equipe COM – OBMEP
Julho de 2020.
[1] A Matemática do Ensino Médio, volume 2: Coleção do Professor de Matemática – Elon Lages Lima; Paulo Cesar Pinto Carvalho; Eduardo Wagner e Augusto César Morgado.
[2] Análise Combinatória e Probabilidade: Coleção do Professor de Matemática – Augusto César Morgado; João Bosco Pitombeira de Carvalho; Paulo Cesar Pinto Carvalho e Pedro Fernandez.
[3] Aulete Digital (Último acesso em 15/06/20)
[4] Fundamentos de Matemática Elementar, volume 5 – Samuel Hazzan.
[5] Introdução à Teoria das Probabilidades – Prof. Victor Hugo Lachos Davila. (Último acesso em 15/06/20)
[6] Matemática, volume único – Gelson Iezzi; Osvaldo Dolce; David Mauro Degenszajn; Roberto Périgo.
[7] Wikipedia (Último acesso em 15/06/20)
[8] YouTube (Último acesso em 15/06/20)