.Sala de Estudo: Diagrama de Venn

De modo geral, um diagrama é uma representação visual simplificada de um determinado conceito ou ideia. Vamos explorar nesta Sala um tipo de diagrama bastante utilizado na Matemática: Diagrama de Venn.
Esses diagramas podem ajudar a entender melhor as operações entre conjuntos, bem como a perceber algumas de suas propriedades. Também são utilizados como representações gráficas de enunciados relacionados a problemas de raciocínio lógico, já que esse tipo de representação permite explorar as relações existentes entre as diversas partes que compõem uma proposição ou um enunciado.
Os Diagramas de Venn têm o nome de seu criador, John Venn – matemático e lógico inglês que viveu de 1834 a 1923.

John Venn
Imagem extraída do MacTutor History of Mathematics
(Último acesso em 28/06/20)

No dia 4 de agosto de 2014, o Google homenageou os 180 anos do nascimento de John Venn com um de seus doodles (Versões modificadas do logotipo do Google, usadas para feriados, aniversários de pessoas famosas e eventos importantes.). Na imagem podemos observar uma representação típica da interseção de dois conjuntos, conforme discutiremos mais adiante.

Imagem extraída do Guia do Estudante
(Último acesso em 28/06/20)

Nesta Sala, vamos apresentar os diagramas de Venn para utilizá-los na visualização e no entendimento de propriedades de conjuntos, bem como na solução de alguns problemas de raciocínio lógico.

Mas afinal, o que são os Diagramas de Venn?

Diagramas de Venn são representações esquemáticas que permitem visualizarmos conjuntos como se fossem regiões do plano. A partir do interior de um retângulo, que representará o conjunto universo (o conjunto de todos os elementos possíveis) de uma dada discussão, os vários conjuntos envolvidos são limitados por figuras fechadas como círculos, quadrados, retângulos, losangos. O interior de cada figura representa, simbolicamente, os elementos do respectivo conjunto. (No caso de um conjunto finito com poucos elementos, esses elementos podem ser dispostos na região do plano limitada pela figura que o representa.)
Independentemente de os conjuntos serem finitos ou infinitos, podemos indicar graficamente conceitos elementares que envolvam um número finito de conjuntos e as diferentes relações existentes entre eles.

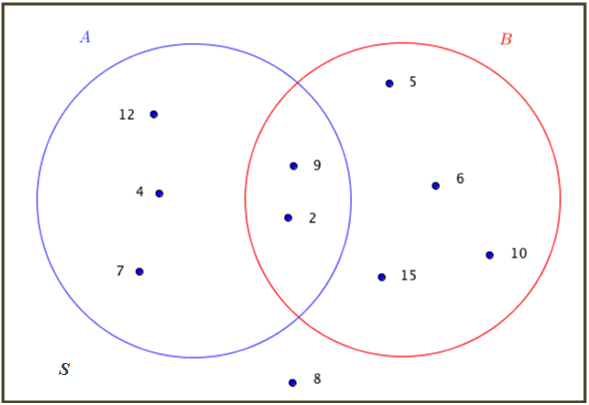
• Por exemplo, na figura abaixo temos a representação dos conjuntos [tex]A = \{2, 4, 7, 9, 12\}[/tex], [tex]B = \{2, 5, 6, 9, 10, 15\}[/tex] e [tex]S =\{2, 4, 5, 6, 7, 8, 9, 10, 12, 15\}[/tex] por meio de diagramas de Venn.

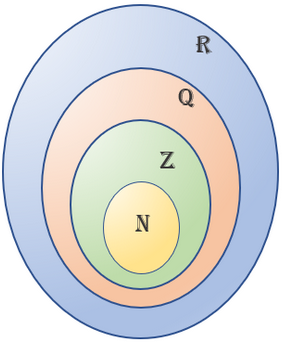
• Outro exemplo. Na próxima imagem, utilizamos diagramas de Venn para representar os conjuntos infinitos [tex]\mathbb{N}[/tex] (conjunto dos números naturais), [tex]\mathbb{Z}[/tex] (conjunto dos números inteiros), [tex]\mathbb{Q}[/tex] (conjunto dos números racionais) e [tex]\mathbb{R}[/tex] (conjunto dos números reais), explicitando a relação de inclusão entre eles.

• O próximo exemplo foi adaptado de uma questão da VUNESP/2011 (Concurso TJM-SP – Analista de Sistemas (Judiciário)).
  O diagrama da próxima figura mostra a relação dos seguintes conjuntos:
  
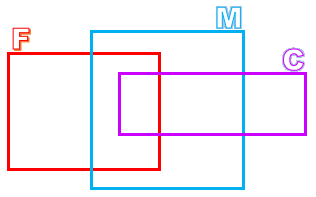
  • C: o conjunto das pessoas que são cantores;
  • F: o conjunto das pessoas felizes;
  • M: o conjunto das pessoas que são músicos.

  De acordo com esse diagrama, pode-se afirmar que:

  (a) todos os músicos são felizes.
  (b) não há cantores que são músicos e felizes.
  (c) os cantores que não são músicos são felizes.
  (d) os felizes que não são músicos não são cantores.
  (e) qualquer músico feliz é cantor.

Se você ficou curioso(a), a alternativa correta é a (d).

Equipe COM – OBMEP