 |
Qual é a área de um triângulo equilátero inscrito em uma circunferência de raio [tex]R[/tex]? |
|
[tex]\dfrac{base\cdot altura}{2}[/tex] |
 |
 |
A fórmula que você apresentou está correta, mas observe que você não conhece a base e a altura do triângulo em questão… |
|
Como assim?????? |
 |
O problema está fornecendo apenas o raio da circunferência na qual o triângulo está inscrito; assim, precisamos de uma fórmula que forneça a área do triângulo em função apenas do raio. |

 |
Não se preocupe! |
Área de um triângulo equilátero

A fórmula mais conhecida para o cálculo da "área de um triângulo qualquer" (ou, mais rigorosamente, "área de uma região triangular") é, de fato,
✐ [tex]\boxed{A_t=\dfrac{base \cdot altura}{2}}[/tex].
No entanto, existem outras fórmulas que nos fornecem essa área, entre elas a de Herão (ou Heron):
✐ [tex]\boxed{A_t=\sqrt{p(p-a)(p-b)(p-c)}}[/tex], sendo [tex]a,\, b,\, c[/tex] os comprimentos dos lados do triângulo e [tex]p=\dfrac{a+b+c}{2}[/tex] o semiperímetro do triângulo.
Vamos tomar dois caminhos diferentes e fazer duas soluções para o problema proposto: cada uma utilizando uma das fórmulas apresentadas.
Solução 1
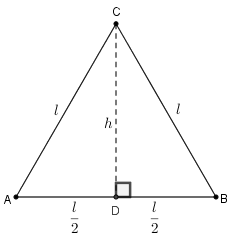
Sabemos que em um triângulo equilátero toda altura é também uma mediana; assim conseguimos relacionar os comprimentos das alturas com os comprimentos dos lados.
Seja, então, [tex]ABC[/tex] um triângulo equilátero cujos lados medem [tex]l[/tex] e, a altura, [tex]h[/tex].
Como a altura [tex]\overline{CD}[/tex] é também a mediana relativa ao lado [tex]\overline{AB}[/tex], do Teorema de Pitágoras, segue que:
[tex]\qquad l^2=h^2+\left(\dfrac{l}{2}\right)^2[/tex]
[tex]\qquad h^2=l^2-\left(\dfrac{l}{2}\right)^2[/tex]
[tex]\qquad h^2=\dfrac{3l^2}{4}[/tex]
[tex]\qquad\boxed{ h=\dfrac{l\sqrt{3}}{2}}[/tex].
Com isso, a fórmula [tex]A_t=\dfrac{base \cdot altura}{2}[/tex] para a área de um triângulo equilátero de lados com comprimento [tex]l[/tex] pode ser assim reescrita:
[tex]\qquad A_{teq}=\dfrac{l\cdot\dfrac{l\sqrt{3}}{2}}{2}=\dfrac{l^2\cdot\sqrt{3}}{4}. \qquad \color{#800000}{(i)}[/tex]
O problema não fornece o valor de [tex] l[/tex], assim, devemos encontrar uma relação entre o lado [tex] l[/tex] de um triângulo equilátero e o raio [tex] R[/tex] da circunferência na qual o triângulo está inscrito. Será o nosso próximo passo e para isso utilizaremos um pouco de trigonometria.
Consideremos, então, o triângulo equilátero [tex]ABC[/tex] inscrito em uma circunferência de centro [tex]O[/tex] e raio [tex] R[/tex]. Sabemos que os ângulos internos de um triângulo equilátero medem [tex]60^\circ[/tex] cada, assim, o ângulo central [tex]A\hat{O}B[/tex], relativo ao ângulo inscrito [tex]A\hat{C}B[/tex], mede [tex]120^\circ[/tex]. (Se você não se lembra da relação entre as medidas de um ângulo inscrito em uma circunferência e de seu respectivo ângulo central, visite esta Sala mais tarde.) Portanto, o triângulo isósceles [tex]AOB[/tex] define ângulos de base medindo [tex]30^\circ[/tex].
Dessa forma, se [tex]D[/tex] é, uma vez mais, o ponto médio do lado [tex]\overline{AB}[/tex], como o triângulo [tex]AOB[/tex] é isósceles, temos que os triângulos [tex]ODB[/tex] e [tex]ODA[/tex] são triângulos retângulos.
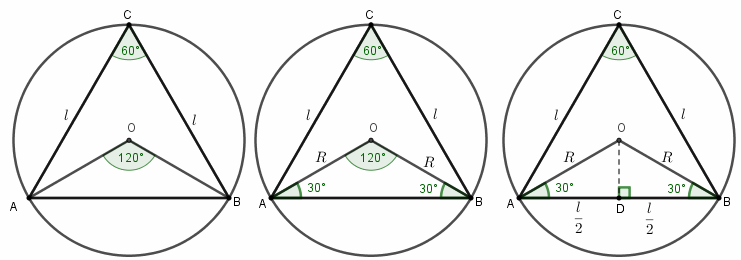
Analisando um dos triângulos retângulos [tex]ODB[/tex] ou [tex]ODA[/tex] e utilizando relações trigonométricas em triângulos retângulos, temos que
[tex]\quad \cos 30^\circ=\dfrac{\frac{l}{2}}{R}[/tex].
Assim, como [tex]\cos 30^\circ=\dfrac{\sqrt{3}}{2}\, [/tex], segue que [tex] \dfrac{\sqrt{3}}{2}=\dfrac{l}{2R}[/tex] ou, ainda, [tex]\boxed{l=\sqrt{3}R}[/tex].[tex]\qquad \color{#800000}{(ii)}[/tex]
Substituindo esse valor de [tex]l[/tex] em [tex]\color{#800000}{(i)}[/tex], obtemos:
[tex]\qquad A_{teq}=\dfrac{l^2\cdot\sqrt{3}}{4}=\dfrac{\left(\sqrt{3}R\right)^2\cdot\sqrt{3}}{4}=\dfrac{3\cdot R^2\cdot \sqrt{3}}{4}[/tex].
Dessa forma, a área de um triângulo equilátero inscrito em uma circunferência de raio [tex]R[/tex] é dada por [tex]\, \fcolorbox{black}{#adcf97}{$\dfrac{3\cdot R^2\cdot \sqrt{3}}{4}$}\, [/tex].
Solução 2
A fórmula geral de Herão para triângulos, [tex]A_{t}=\sqrt{p(p-a)(p-b)(p-c)}\, [/tex], fica bastante simplificada para triângulos equiláteros de lados com comprimento [tex]l[/tex] como o nosso:
[tex]\quad A_{teq}=\sqrt{p(p-l)(p-l)(p-l)}[/tex]
[tex]\quad A_{teq}=\sqrt{p(p-l)^3}[/tex].
Triângulos equiláteros com lados de comprimento [tex]l[/tex] têm semiperímetro [tex]\boxed{p=\dfrac{l+l+l}{2}=\dfrac{3l}{2}}[/tex], assim:
[tex]\quad A_{teq}=\sqrt{\dfrac{3l}{2}\left(\dfrac{3l}{2}-l\right)^3}[/tex]
[tex]\quad A_{teq}=\sqrt{\dfrac{3l}{2}\left(\dfrac{l}{2}\right)^3}[/tex]
[tex]\quad A_{teq}=\sqrt{3\left(\dfrac{l}{2}\right)^4}[/tex]
[tex]\quad \boxed{A_{teq}=\dfrac{l^2\sqrt{3}}{4}}\, [/tex].[tex]\qquad \color{#800000}{(iii)}[/tex]
Já temos a relação entre o lado [tex]l[/tex] do nosso triângulo equilátero e o raio [tex]R[/tex] da circunferência; logo, por [tex]\color{#800000}{(ii)}[/tex] e [tex]\color{#800000}{(iii)}[/tex], segue que [tex]A_{teq}=\dfrac{\left(\sqrt{3}R\right)^2\sqrt{3}}{4}[/tex], ou seja, [tex]\, \fcolorbox{black}{#adcf97}{$A_{teq}=\dfrac{3\cdot R^2\cdot \sqrt{3}}{4}$}\, [/tex].
 |
Para ver uma demonstração da fórmula de Herão, clique AQUI. |
Equipe COM – OBMEP
Outubro de 2019.
 |
Se for conveniente, você pode obter um arquivo PDF desta página. |
