Fórmula de Herão
A partir da conhecida fórmula para o cálculo da área do triângulo, [tex]A_t=\dfrac{base \cdot altura}{2}[/tex], podemos deduzir uma fórmula que nos fornece a área de um triângulo, a partir dos seus elementos mais básicos: a medida de seus lados.
Essa fórmula é atribuída a "Herão de Alexandria"(ou Heron ou Hero) e nos garante que, em um triângulo [tex]ABC[/tex] qualquer, a área [tex]A_t[/tex] é dada por:
✐ [tex]\boxed{A_t=\sqrt{p(p-a)(p-b)(p-c)}}[/tex], sendo [tex]a,\, b,\, c[/tex] os comprimentos dos lados e [tex]p=\dfrac{a+b+c}{2}[/tex] o semiperímetro do triângulo em questão.
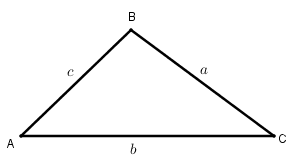
Fixemos o vértice de [tex]ABC[/tex] que define o ângulo interno com a maior medida, digamos [tex]B[/tex], e seja [tex]h[/tex] a medida da altura do triângulo [tex]ABC[/tex], relativa a esse vértice. Consideremos que essa altura divide o lado oposto ao vértice [tex]B[/tex] em dois segmentos cujas medidas são [tex]x[/tex] e [tex]b-x[/tex], conforme figura ao lado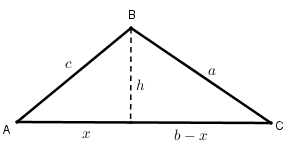 .
.
Pelo Teorema de Pitágoras, temos que
[tex]\qquad a^2=h^2+\left(b-x\right)^2=h^2+b^2-2bx+x^2. \qquad \color{#800000}{(i)}[/tex]
Ainda pelo Teorema de Pitágoras, temos que [tex]c^2=x^2+h^2[/tex], logo,
[tex]\qquad c^2-h^2=x^2\qquad \color{#800000}{(ii)}[/tex]
e
[tex]\qquad x=\sqrt{c^2-h^2}.\qquad \color{#800000}{(iii)}[/tex]
Dessa forma, por [tex] \color{#800000}{(i)}[/tex], [tex] \color{#800000}{(ii)}[/tex] e [tex] \color{#800000}{(iii)}[/tex], podemos afirmar que:
[tex]\qquad a^2=h^2+b^2-2\cdot b\cdot \sqrt{c^2-h^2}+\left(c^2-h^2\right) [/tex]
[tex]\qquad a^2=b^2-2\cdot b\cdot \sqrt{c^2-h^2}+c^2 [/tex]
[tex]\qquad 2\cdot b\cdot \sqrt{c^2-h^2}=b^2+c^2 -a^2 [/tex]
[tex]\qquad \sqrt{c^2-h^2}=\dfrac{b^2+c^2 -a^2}{2b}[/tex]
[tex]\qquad c^2-h^2=\left(\dfrac{b^2+c^2 -a^2}{2b}\right)^2[/tex]
[tex]\qquad h^2=c^2-\left(\dfrac{b^2+c^2 -a^2}{2b}\right)^2. \qquad \color{#800000}{(iv)}[/tex]
Como [tex]A_t=\dfrac{base \cdot altura}{2}[/tex], então [tex]\left(A_t\right)^2=\dfrac{b^2\cdot h^2}{4}[/tex]; assim, utilizando [tex] \color{#800000}{(iv)}[/tex], segue que:
[tex]\qquad A_t^2=\dfrac{b^2 \left( c^2-\left(\dfrac{b^2+c^2 -a^2}{2b}\right)^2\right)}{4}=\dfrac{b^2 \left( c^2-\dfrac{\left(b^2+c^2 -a^2\right)^2}{\left(2b\right)^2}\right)}{4}[/tex]
[tex]\qquad A_t^2=\dfrac{\cancel{b^2} \left( 4b^2c^2-\left(b^2+c^2 -a^2\right)^2\right)}{4\cdot 4 \cdot \cancel{b^2}}=\dfrac{ 4b^2c^2-\left(b^2+c^2 -a^2\right)^2}{16}[/tex]
[tex]\qquad A_t^2=\dfrac{ \left(2bc \right)^2-\left(b^2+c^2 -a^2\right)^2}{16}. \qquad \color{#800000}{(v)}[/tex]
Por um momento, façamos [tex]\boxed{z=2bc}\, [/tex] e [tex]\, \boxed{y=b^2+c^2 -a^2}[/tex]. Assim, de [tex] \color{#800000}{(v)}[/tex], segue que:
[tex]\qquad A_t^2=\dfrac{ z^2-y^2}{16}=\dfrac{(z+y)\, (z-y)}{16}[/tex]
e, portanto,
[tex]\qquad A_t^2=\dfrac{(\, \overbrace{\, 2bc\, }^{z}+\, \overbrace{b^2+c^2 -a^2}^{y}\, )\, (\, \overbrace{\, 2bc\, }^{z}-(\, \overbrace{b^2+c^2 -a^2}^{y}\, ))}{16}\\
\qquad A_t^2=\dfrac{(2bc+b^2+c^2 -a^2)\, (2bc-b^2-c^2 +a^2)}{16}[/tex]
[tex]\qquad A_t^2=\dfrac{((b^2+2bc+c^2) -a^2)\, (-(b^2-2bc+c^2) +a^2)}{16}[/tex]
[tex]\qquad A_t^2=\dfrac{((b+c)^2 -a^2)\, (-(b-c)^2 +a^2)}{16}[/tex]
[tex]\qquad A_t^2=\dfrac{((b+c)^2 -a^2)\, (a^2-(b-c)^2)}{16}.\qquad \color{#800000}{(vi)}[/tex]
Façamos, agora, [tex]\boxed{q=b+c}\, [/tex] e [tex]\, \boxed{k=b-c}[/tex]. De [tex] \color{#800000}{(vi)}[/tex], segue que:
[tex]\qquad A_t^2=\dfrac{(q^2 -a^2)\, (a^2-k^2)}{16}=\dfrac{((q+a)(q-a))\, ((a+k)(a-k))}{16}[/tex]
[tex]\qquad A_t^2=\dfrac{(q+a)(q-a)(a+k)(a-k)}{16}[/tex]
e, dessa forma,
[tex]\qquad A_t^2=\dfrac{(\, \overbrace{b+c}^{q}+a)(\, \overbrace{b+c}^{q}-a)\, (a+\overbrace{b-c}^{k})(a-(\, \overbrace{b-c}^{k}))}{16}[/tex]
[tex]\qquad A_t^2=\dfrac{(b+c+a)\cdot(b+c-a)\cdot(a+b-c)\cdot(a-b+c)}{16}[/tex]
[tex]\qquad A_t^2=\dfrac{b+c+a}{2}\, \cdot\, \dfrac{b+c-a}{2}\, \cdot\, \dfrac{a+b-c}{2}\, \cdot\, \dfrac{a-b+c}{2}\qquad \color{#800000}{(vii)}[/tex]
Note que, se [tex]\boxed{p=\dfrac{a+b+c}{2}}[/tex], então:
- [tex]\boxed{\dfrac{b+c-a}{2}}=\dfrac{b+c-a+(a-a)}{2}=\dfrac{b+c+a-2a}{2}=\dfrac{b+c+a}{2}-\dfrac{2a}{2}=\boxed{p-a}[/tex]
- [tex]\boxed{\dfrac{a+b-c}{2}}=\dfrac{a+b-c+(c-c)}{2}=\dfrac{a+b+c-2c}{2}=\dfrac{a+b+c}{2}-\dfrac{2c}{2}=\boxed{p-c}[/tex]
- [tex]\boxed{\dfrac{a-b+c}{2}}=\dfrac{a-b+c+(b-b)}{2}=\dfrac{a+c+b-2b}{2}=\dfrac{a+c+b}{2}-\dfrac{2b}{2}=\boxed{p-b}[/tex]
logo, segue de [tex] \color{#800000}{(vii)}[/tex] que:
[tex]\qquad A_t^2=p\cdot(p-a)\cdot(p-c)\cdot(p-b)=p\cdot(p-a)\cdot(p-b)\cdot(p-c)[/tex],
donde, finalmente,
[tex]\qquad \, \fcolorbox{black}{#adcf97}{$A_t=\sqrt{p\, (p-a)\, (p-c)\, (p-b)}$}[/tex].
Equipe COM – OBMEP
Novembro de 2017.
 |
Se for conveniente, você pode obter um arquivo PDF desta página. |
