Trigonometria do triângulo retângulo
 |
Discutiremos nesta sala as propriedades iniciais da trigonometria do triângulo retângulo.
|
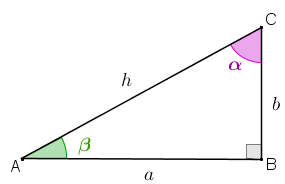
Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a, \, b, \, h[/tex], respectivamente e um dos ângulos agudos com medida [tex]\theta[/tex], [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].

Nessas condições, chamamos de:
● tangente de [tex]\theta[/tex], e denotamos por [tex]tg \, \theta[/tex], a razão entre os comprimentos do cateto oposto e do cateto adjacente a [tex]\theta[/tex]:
[tex]\qquad\qquad tg \, \theta= \dfrac{a}{b}[/tex];
● seno de [tex]\theta[/tex], e denotamos por [tex]sen \, \theta[/tex], a razão entre os comprimentos do cateto oposto a [tex]\theta[/tex] e da hipotenusa:
[tex]\qquad\qquad sen \, \theta= \dfrac{a}{h}[/tex];
● cosseno de [tex]\theta[/tex], e denotamos por [tex]cos \, \theta[/tex], a razão entre os comprimentos do cateto adjacente a [tex]\theta[/tex] e da hipotenusa:
[tex]\qquad\qquad cos \, \theta= \dfrac{b}{h}[/tex].
 |
Nesta sala, além de reapresentar as propriedades iniciais da trigonometria do triângulo retângulo, vamos justificá-las matematicamente e comentá-las.
|
|
Isso significa que para cada propriedade vamos fazer uma demonstraçãozinha, não é? |
 |
 |
Isso mesmo! Afirmações matemáticas carecem de justificativas para que sejam consideradas válidas. Particularmente as justificativas que faremos são muito simples de serem entendidas.
|
Para justificativas mais sofisticadas é necessário uma linguagem mais sofisticada, também.
Se vocês têm dificuldades com o uso de linguagem matemática, cliquem no próximo botão e aprendam um pouco mais…
Bom proveito, pessoal ! ! !
Propriedades iniciais da trigonometria do triângulo retângulo

Propriedade 1: Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a, \, b, \, h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
Nessas condições, são válidas as seguintes propriedades:
a) [tex]sen^2\theta + cos^2\theta = 1 \qquad\qquad[/tex]b) [tex]\dfrac{sen \, \theta}{cos \, \theta} = tg \, \theta[/tex].
|
|
|
Propriedade 2: Considerem dois ângulos agudos complementares com medidas [tex]\alpha[/tex] e [tex]\beta[/tex].
Então:
a) [tex] \, sen \, \alpha = cos \, \beta \, \, \, \, \, \, \, \, \qquad\qquad[/tex]b) [tex] \, tg \, \alpha = \dfrac{1}{tg \, \beta}[/tex].
|
|
|
Então:
a)[tex] \, sen \, 2\theta=2sen\theta \cdot cos\theta\qquad\qquad[/tex]b) [tex]sen \, \dfrac{\theta}{2}=\sqrt{\dfrac{1-cos \, \theta}{2}}[/tex].
|
|
|
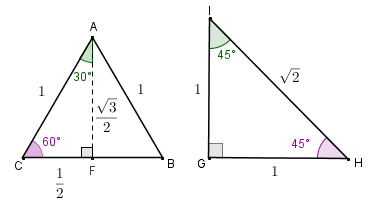
a) [tex] \, \, sen \, 30^{\circ}=\dfrac{1}{2}\qquad\qquad[/tex] [tex] \, \, \, \, cos \, 30^{\circ}=\dfrac{\sqrt{3}}{2}\qquad\qquad[/tex] [tex] tg \, 30^{\circ}=\dfrac{\sqrt{3}}{3}[/tex] .
b) [tex] \, \, sen \, 45^{\circ}=\dfrac{\sqrt{2}}{2}\qquad\qquad[/tex] [tex] cos \, 45^{\circ}=\dfrac{\sqrt{2}}{2}\qquad\qquad[/tex] [tex] tg \, 45^{\circ}=1[/tex] .
c) [tex] \, \, sen \, 60^{\circ}=\dfrac{\sqrt{3}}{2}\qquad\qquad[/tex] [tex] cos \, 60^{\circ}=\dfrac{1}{2}\qquad\qquad[/tex] [tex] \, \, \, \, tg \, 60^{\circ}=\sqrt{3}[/tex] .
|
|
|
Bons estudos!
Equipe COM – OBMEP

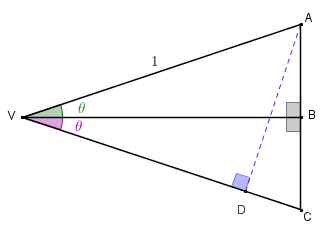 ● Com a informação de que [tex]\overline{VA} \, [/tex] e [tex]\overline{VC} \, [/tex] são segmentos de comprimento [tex]1[/tex], a figura por si só justifica a primeira igualdade. Mas, aí vai uma dica:
● Com a informação de que [tex]\overline{VA} \, [/tex] e [tex]\overline{VC} \, [/tex] são segmentos de comprimento [tex]1[/tex], a figura por si só justifica a primeira igualdade. Mas, aí vai uma dica: