Sala de Estudos: Matrizes

Um pouco de História

Há pouco mais de 150 anos, o estudo das matrizes tomou maiores proporções. O primeiro matemático a lhes dar um nome parece ter sido Augustin-Louis Cauchy (1789 – 1857), em 1826. Porém, o nome matriz só veio com James Joseph Sylvester (1814-1897), em 1850. Seu amigo Arthur Cayley (1821–1895), com sua famosa Memoir on the Theory of Matrices, de 1858, divulgou esse nome e iniciou a demonstrar sua utilidade.

Imagem extraída de O Baricentro da Mente.

Cayley introduziu as matrizes para simplificar a notação de uma transformação linear. A observação do efeito de duas transformações sucessivas sugeriu a definição de produto de matrizes. Daí chegou à ideia de inversa de uma matriz, o que obviamente pressupõe a de elemento neutro (no caso, a matriz identidade). Mais tarde, Cayley introduziu o conceito de adição de matrizes e o de multiplicação de matrizes por escalares, chamando a atenção para as propriedades algébricas dessas operações.

Ao desenvolver a teoria das matrizes, como outros assuntos, a grande preocupação de Cayley era a forma e a estrutura em álgebra. O século XIX se encarregaria de encontrar inúmeras aplicações para suas matrizes.

Mas onde as matrizes são aplicadas na minha vida?

Em matemática, uma matriz é uma representação de dados em linhas e colunas. Em outras palavras, é uma tabela retangular de números, símbolos ou expressões, sendo seus elementos organizados em linhas e colunas. Engana-se muito quem acredita que o estudo das matrizes não tem aplicação e importância na vida cotidiana da humanidade. Vamos apresentar algumas dessas aplicações: são diversos os graus de utilidade, de jogos a aplicações médicas!

Tabuleiro de Xadrez

Ele possui 64 casas, divididas em 8 colunas e 8 linhas. O tabuleiro de xadrez pode ser representado por uma matriz, onde cada uma de suas casas pode ser identificada por uma letra e um número. Cada jogada pode ser indicada pela letra da peça, mais a coordenada da casa de destino. Por exemplo, Be5 significa bispo se move para e5, a casa da coluna e e da linha 5.

Imagem extraída de Wikipedia.

Batalha Naval

Dois jogadores devem posicionar suas embarcações em determinadas posições de uma matriz (o tabuleiro) e cada um deve indicar uma posição para atacar e tentar afundar as embarcações do oponente.

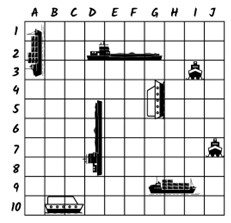Imagem extraída de Conexão Escola.

Pixels e telas

O pixel é definido como a menor parte de uma imagem. Eles são pequenos quadradinhos que possuem informações relacionadas a cores, cuja junção é o que nos permite enxergar imagens em telas eletrônicas. Quanto mais pixels, melhor a qualidade da imagem. O interessante sobre esses “quadradinhos” é que eles estão dispostos em matrizes, e desse modo, quanto maior a matriz, melhor a qualidade da imagem.

Imagem extraída de Matreemática.

Teoria dos Grafos

A teoria dos grafos é basicamente o estudo das relações entre objetos e conjuntos. A base para a teoria dos grafos são as matrizes e suas aplicações são diversas: análise de influências entre pessoas, jogos de xadrez, distribuição de redes de água e esgoto para uma população e outros problemas famosos, como o Problema do Caixeiro Viajante, que consiste em analisar uma forma otimizada do caminho que ele faria em uma viagem, começando num ponto e terminando a viagem nele, só que passando por todos os outros pontos apenas uma vez.

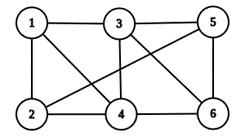Grafo: Imagem extraída de WikiMat.

Computação Gráfica

Na computação gráfica, o uso de matrizes é muito utilizado em diversas aplicações. Figuras tridimensionais em um monitor de computador ou celulares só são possíveis graças a uma matriz que é gerada pelo processamento da imagem na tela. Consequentemente podemos fazer com que um objeto em 3 dimensões seja projetado no monitor e a álgebra de matrizes possibilita com que novas imagens possam ser geradas do mesmo objeto por meio da rotação, translação, alterando sua escala, etc.

Imagem extraída de Freepik.

Tomografia Computadorizada

O objetivo de um exame de tomografia é construir a imagem de um corte transversal de um corpo humano a partir da análise do escaneamento por raios X. Como já citado, o pixel é o menor ponto da imagem que pode ser obtido. Portanto, uma imagem é formada por uma certa quantidade de pixels. O conjunto de pixels está distribuído em colunas e linhas que formam a matriz de imagem da tomografia. O valor atribuído a cada entrada desta matriz está relacionado com a quantidade de radiação que chegou neste ponto.

Imagem extraída de Saúde iD.

Criptografia

É o estudo de codificar ou decodificar mensagens a fim de torná-las secretas. Este método é muito antigo e já era utilizado desde os tempos do império romano. Atualmente, o uso da criptografia evoluiu e consequentemente aumentou o interesse no assunto devido à necessidade de manter a privacidade da informação que nós acessamos. Sem ela, nossas senhas de redes sociais, dispositivos, contas bancárias, entre outras, seriam facilmente decifradas e não teríamos nenhuma segurança de nossas informações. Uma forma de utilizar matrizes na criptografia é utilizar inversão de matrizes para descriptografar.

Imagem extraída de Freepik.

Controle de Tráfego

A figura abaixo representa um cruzamento de duas ruas de mão dupla, cujo fluxo de automóveis nos pontos A, B e C é definido por três conjuntos de semáforos.

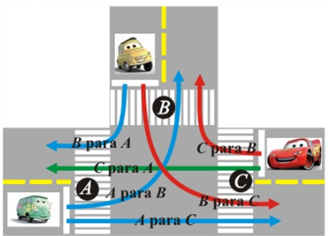Imagem extraída de O Baricentro da Mente.

As matrizes [tex]M_1[/tex], [tex]M_2[/tex] e [tex]M_3[/tex] indicam o tempo, em minutos, durante o qual os semáforos se mantêm simultaneamente abertos segundo a sequência dada:

Inicialmente, durante um minuto, ficam verdes os semáforos de A para B, de A para C e de B para A.

Em seguida, durante meio minuto, ficam verdes os semáforos de B para A, de B para C e de C para B.

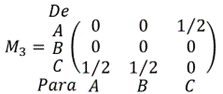
E, finalmente, durante meio minuto, ficam verdes os semáforos de C para A, de C para B e de A para C.
A matriz [tex]M[/tex] é obtida somando-se [tex]M_1[/tex], [tex]M_2[/tex] e [tex]M_3[/tex] termo a termo e mostra o tempo que cada semáforo fica aberto em cada sentido no período de dois minutos.

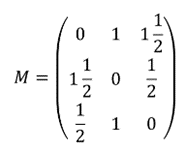
Podemos observar, por exemplo, que o semáforo de B para A fica aberto durante um minuto e meio a cada período de dois minutos.
Se multiplicarmos todos os termos da matriz [tex]M[/tex] por [tex]30[/tex], já que o período é de dois minutos, obteremos o tempo, em minutos, que cada semáforo fica aberto durante uma hora:

[tex]N=30 \cdot M[/tex]

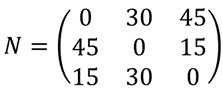
Neste exemplo hipotético, sabe-se que nestas ruas é possível passar até [tex]20[/tex] carros por minuto cada vez que os semáforos abrem. Assim, se multiplicarmos por [tex]20[/tex] todos os termos da matriz [tex]N[/tex], teremos a quantidade máxima de carros que podem passar por este cruzamento no período de uma hora.

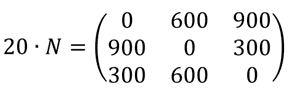
Se o número de carros em alguma das direções for maior que a quantidade máxima possível, teremos um engarrafamento, que poderá ou não ser resolvido alterando-se os tempos de abertura dos semáforos, isto é, modificando-se os valores das matrizes [tex]M_1, M_2[/tex] e [tex]M_3[/tex].

Se você ficou confuso com o último exemplo, não se preocupe! Você entenderá melhor a notação e as operações após terminarmos nosso passeio pelo mundo das matrizes. Vamos lá?

Vamos estudar a Matemática das Matrizes

CONCEITO

Como dito anteriormente, as matrizes são um conjunto de números ou símbolos distribuídos de forma retangular em filas verticais e horizontais, de modo que seus elementos sejam dispostos em linhas e colunas. Uma matriz é comumente utilizada para a organização de dados tabulares a fim de facilitar a resolução de problemas.

O conjunto das matrizes é uma estrutura matemática munida das operações de adição, subtração e multiplicação e de propriedades, como elemento neutro e inverso, o que possibilita a aplicação das matrizes em diversos campos do conhecimento.

Representação de uma Matriz

As matrizes são sempre representadas por letras maiúsculas ([tex]A, B, C, \cdots [/tex]), que são acompanhadas por índices, nos quais o primeiro número indica a quantidade de linhas, e o segundo, o número de colunas.

Denominamos [tex]m \times n[/tex] a ordem ou tipo da matriz. Filas horizontais são denominadas linhas e filas verticais são denominadas colunas. Também representamos uma matriz na escrita com utilização de seus elementos entre parênteses, colchetes ou duas barras verticais de cada lado.

Os elementos da matriz são denominados de entradas da matriz e obedecem uma regra de localização dentro da mesma. Veja:

[tex]\qquad A=\begin{pmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\
a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn}
\end{pmatrix}.
[/tex]

Em uma linguagem mais formal, podemos escrever a matriz assim:

[tex]\qquad A=(a_{ij})_{m \times n}[/tex], onde [tex]1 \leq i \leq m[/tex] e [tex]1 \leq j \leq n[/tex], com [tex]i, j \in \mathbb{Z}[/tex].

Cada entrada da matriz possui índices [tex]i[/tex] e [tex]j[/tex] que indicam, respectivamente, a posição da linha e da coluna. Desse modo, [tex]a_{11}[/tex] é o elemento da primeira linha e primeira coluna, [tex]a_{53}[/tex] é o elemento da quinta linha e terceira coluna e assim sucessivamente.

Construção de uma Matriz por uma Lei de Formação

Em geral, podemos construir uma matriz por meio de uma lei de formação previamente dada.

Igualdade de Matrizes

Duas matrizes, [tex]A=(a_{ij})_{m \times n}[/tex] e [tex]B=(b_{ij})_{m \times n}[/tex] são iguais quando [tex]a_{ij}=b_{ij}[/tex] para todo [tex]i \in \{1, 2, 3, \cdots, m\}[/tex] e todo [tex]j \in \{1, 2, 3, \cdots, n\}[/tex]. Em outras palavras, duas matrizes são iguais quando possuem mesma ordem e seus elementos são ordenadamente iguais.

TIPOS DE MATRIZES

Existem diversos tipos de matrizes. Vamos estudar alguns dos principais aqui nessa sala.

1. Matriz Quadrada

É uma matriz na qual a quantidade de linhas é igual à quantidade de colunas. Nesse caso, dizemos que uma matriz quadrada tem ordem [tex]n \times n[/tex] ou simplesmente ordem [tex]n[/tex].
Toda matriz quadrada possui duas diagonais: a principal e a secundária. A diagonal principal de uma matriz [tex]A_{n\times n}[/tex] é a coleção dos elementos [tex]a_{ij}[/tex] da matriz em que [tex]i=j[/tex]. A diagonal secundária dessa matriz é formada pelos elementos [tex]a_{ij}[/tex] em que [tex]i+j=n+1[/tex].

2. Matriz Unitária

É uma matriz de ordem um, ou seja, possui uma linha e uma coluna e, portanto, apenas um elemento.

3. Matriz Nula

É uma matriz na qual todas as entradas são nulas. Geralmente representamos a matriz nula pela letra [tex]O[/tex].

4. Matriz Linha

É uma matriz que possui apenas uma linha.

5. Matriz Coluna

É uma matriz que possui apenas uma coluna.

6. Matriz Triangular

É uma matriz quadrada em que todos os elementos que estão acima (Triangular Inferior) ou abaixo (Triangular Superior) da diagonal principal são iguais a zero.

7. Matriz Diagonal

A matriz diagonal é um caso particular de matriz triangular. Os termos que estão acima ou abaixo da diagonal principal são todos iguais a zero. Em outras palavras, uma matriz diagonal é uma matriz triangular tanto superior quanto inferior.

8. Matriz Oposta

É a matriz obtida quando trocamos todos os sinais dos elementos da matriz original.

9. Matriz Transposta

Dada uma matriz [tex]A=(a_{ij})_{m \times n}[/tex], chama-se transposta de [tex]A[/tex] a matriz [tex]A^t=(a’_{ij})_{n \times m}[/tex] tal que [tex]a’_{ji}=a_{ij}[/tex], para todo [tex]i[/tex] e todo [tex]j[/tex]. Por exemplo, [tex]a’_{11}, a’_{21}, a’_{31}, \cdots, a’_{n1}[/tex] são, respectivamente, iguais a [tex]a_{11}, a_{12}, a_{13}, \cdots, a_{1n}[/tex]. As colunas de [tex]A^t[/tex] são ordenadamente iguais às linhas de [tex]A[/tex].
Assim, transposta é a matriz obtida quando transformamos as linhas de uma matriz em colunas. Nesse caso, se a matriz original possui ordem [tex]m \times n[/tex], sua transposta possuirá ordem [tex]n \times m[/tex].

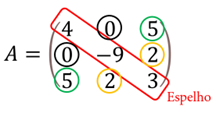
10. Matriz Simétrica

É uma matriz quadrada que é igual à sua transposta:

[tex]\qquad A=A^t.[/tex]

Uma observação interessante sobre uma matriz simétrica, é que a diagonal principal funciona como se fosse um espelho plano para os elementos que equidistam desse espelho. Observe:

11. Matriz Antissimétrica

É uma matriz quadrada cuja transposta é igual à sua oposta:

[tex]\qquad A^t=-A.[/tex]

Uma observação interessante sobre uma matriz antissimétrica, é que a diagonal principal funcional como se fosse um espelho plano onde os elementos que equidistam desse espelho visualizam seus simétricos. Observe:

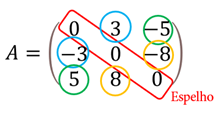
Outra observação importante para esse tipo de matriz é que a diagonal principal só pode ser formada por zeros.

12. Matriz Identidade

Uma matriz identidade é uma matriz diagonal em que os elementos da diagonal principal são iguais a [tex]1[/tex] e os demais elementos são iguais a [tex]0[/tex].

A matriz Identidade será muito importante quando estivermos estudando inversão de matrizes.

OPERAÇÕES COM MATRIZES

Adição

Dadas duas matrizes, [tex]A=(a_{ij})_{m \times n}[/tex] e [tex]B=(b_{ij})_{m \times n}[/tex], chamamos soma [tex]A+B[/tex] a matriz [tex]C=(c_{ij})_{m \times n}[/tex] tal que [tex]c_{ij}=a_{ij}+b_{ij}[/tex], para todo [tex]i[/tex] e todo [tex]j[/tex]. Em outras palavras, a adição de matrizes só pode ser realizada se as matrizes possuírem mesma ordem e a adição é feita ordenadamente entre elementos correspondentes.

Exemplo:
[tex]\qquad \begin{bmatrix}
6 & -2\\
1 & 2\\
-5 & 0
\end{bmatrix}
+
\begin{bmatrix}
5 & 7\\
2 & -8\\
1 & 0
\end{bmatrix}
=
\begin{bmatrix}
6+5 & -2+7\\
1+2 & 2+(-8)\\
-5+1 & 0+0
\end{bmatrix}
=
\begin{bmatrix}
11 & 5\\
3 & -6\\
-4 & 0
\end{bmatrix}.
[/tex]

Subtração

Dadas duas matrizes, [tex]A=(a_{ij})_{m \times n}[/tex] e [tex]B=(b_{ij})_{m \times n}[/tex], chamamos subtração ou diferença [tex]A-B[/tex] a matriz soma de [tex]A[/tex] com a matriz oposta de [tex]B[/tex].

Multiplicação de um escalar por uma Matriz

Dado um número real [tex]k[/tex] e uma matriz [tex]A=(a_{ij})_{m \times n}[/tex], chama-se produto [tex]k\cdot A[/tex] a matriz [tex]B=(b_{ij})_{m \times n}[/tex], tal que [tex]b_{ij}=k \cdot a_{ij}[/tex], [tex]\forall i,j[/tex]. Em outras palavras, multiplicar uma matriz por um número real é obter uma nova matriz na qual todos os elementos da matriz original foram multiplicados pelo número real.

Multiplicação de Matrizes

Dadas duas matrizes, [tex]A=(a_{ij})_{m \times n}[/tex] e [tex]B=(b_{jk})_{n \times p}[/tex], chamamos produto [tex]A \cdot B[/tex] a matriz [tex]C=(c_{ik})_{m \times p}[/tex] tal que

[tex]\qquad c_{ik}= a_{i1} \cdot b_{1k}+ a_{i2} \cdot b_{2k}+ a_{i3} \cdot b_{3k}+ \cdots + a_{in} \cdot b_{nk}, \forall i \in \{1, 2, 3, \cdots, m\}, k \in \{1, 2, 3, \cdots, p\}.[/tex]

É importante observar que a definição dada garante a existência do produto [tex]A \cdot B[/tex] somente se o número de colunas de [tex]A[/tex] for igual ao número de linhas de [tex]B[/tex]. A definição dada também afirma que o produto [tex]A \cdot B[/tex] é uma matriz que tem o número de linhas de [tex]A[/tex] e o número de colunas de [tex]B[/tex], pois [tex]C=A \cdot B[/tex] é da ordem [tex]m \times p[/tex]. Ainda pela definição, um elemento [tex]c_{ik}[/tex] da matriz [tex]A \cdot B[/tex] deve ser obtido pelo procedimento seguinte:
(i) toma-se a linha [tex]i[/tex] da matriz [tex]A[/tex]:

[tex]\qquad a_{i1} \ a_{i2} \ a_{i3} \ \cdots a_{in}[/tex].

(ii) toma-se a coluna [tex]k[/tex] da matriz [tex]B[/tex]

[tex]\qquad
b_{1k}\\
\qquad b_{2k}\\
\qquad b_{3k}\\
\qquad \vdots\\
\qquad b_{nk}
[/tex]

(iii) coloca-se a linha [tex]i[/tex] de [tex]A[/tex] na vertical ao lado da coluna [tex]k[/tex] de [tex]B[/tex] de acordo com o esquema abaixo

[tex]
\qquad a_{i1} \ b_{1k}\\
\qquad a_{i2} \ b_{2k}\\
\qquad a_{i3} \ b_{3k}\\
\qquad \vdots \\
\qquad a_{in} \ b_{nk}
[/tex]

(iv) calculam-se os [tex]n[/tex] produtos dos elementos que ficaram lado a lado conforme abaixo:

[tex]
\qquad a_{i1} \cdot b_{1k}\\
\qquad a_{i2} \cdot b_{2k}\\
\qquad a_{i3} \cdot b_{3k}\\
\qquad \vdots\\
\qquad a_{in} \cdot b_{nk}
[/tex]

(v) somam-se esses [tex]n[/tex] produtos, obtendo [tex]c_{ik}[/tex].

Exemplo:

[tex]\qquad \begin{bmatrix}
1 & 0 & 2\\
2 & 3 & 1
\end{bmatrix}
\cdot \begin{bmatrix}
3\\
2\\
4\end{bmatrix}
=
\begin{bmatrix}
1 \cdot 3+0 \cdot 2+2 \cdot 4\\
2 \cdot 3+3 \cdot 2+1 \cdot 4\\
\end{bmatrix}
=
\begin{bmatrix}
3+0+8\\
6+6+4\\
\end{bmatrix}
=
\begin{bmatrix}
11\\
16\\
\end{bmatrix}.
[/tex]

Inversão de Matrizes

Seja [tex]A[/tex] uma matriz quadrada de ordem [tex]n[/tex]. Dizemos que [tex]A[/tex] é matriz inversível se existir uma matriz [tex]B[/tex] tal que [tex]A \cdot B= B \cdot A=I_n[/tex]. Se [tex]A[/tex] não é inversível, dizemos que é uma matriz singular.

Teorema: Se [tex]A[/tex] é uma matriz inversível, então é única a matriz [tex]B[/tex] tal que [tex]A \cdot B= B \cdot A=I_n[/tex].

Demonstração: Suponha que exista uma matriz [tex]C[/tex] tal que [tex]A \cdot C= C \cdot A=I_n[/tex]. Então:

[tex]C=I_n \cdot C=(B \cdot A) \cdot C=B \cdot (A \cdot C)= B \cdot I_n=B[/tex].

Definição: Dada uma matriz inversível [tex]A[/tex] de ordem [tex]n[/tex], chamamos inversa de [tex]A[/tex] a matriz [tex]A^{-1}[/tex], que é única, tal que [tex]A \cdot A^{-1}= A^{-1} \cdot A=I_n[/tex]. Observe que a matriz [tex]A^{-1}[/tex], quando existe, também é quadrada de ordem [tex]n[/tex].

Dá pra imaginar o trabalhão que dá fazer a inversa de uma matriz quadrada de ordem [tex]3[/tex]? A cada aumento de ordem da matriz, fica mais trabalhoso o cálculo para determinar sua inversa, quando ela existe. O estudo dos determinantes é primordial para a determinação de inversas de matrizes quadradas. O estudo das chamadas matrizes elementares também é muito útil, mas foge do escopo desta sala.

Exercícios Propostos

1. (Enem 2021) Uma construtora, pretendendo investir na construção de imóveis em uma metrópole com cinco grandes regiões, fez uma pesquisa sobre a quantidade de famílias que mudaram de uma região para outra, de modo a determinar qual região foi o destino do maior fluxo de famílias, sem levar em consideração o número de famílias que deixaram a região. Os valores da pesquisa estão dispostos em uma matriz [tex]A=(a_{ij}), i, j \in \{1, 2, 3, 4, 5\}[/tex], em que o elemento [tex]a_{ij}[/tex] corresponde ao total de famílias (em dezenas) que se mudaram da região [tex]i[/tex] para a região [tex]j[/tex] durante um certo período, e o elemento [tex]a_{ii}[/tex] é considerado nulo, uma vez que somente são consideradas mudanças entre regiões distintas. A seguir, está apresentada a matriz com os dados da pesquisa.

[tex]\qquad \begin{bmatrix}
0 & 4 & 2 & 2 & 5 \\
0 & 0 & 6 & 2 & 3 \\
2 & 2 & 0 & 3 & 0 \\
1 & 0 & 2 & 0 & 4 \\
1 & 2 & 0 & 4 & 0
\end{bmatrix}
[/tex]

Qual região foi selecionada para o investimento da construtora?

a) 1
b) 2
c) 3
d) 4
e) 5

2. (Enem 2019) Um professor aplica, durante os cinco dias úteis de uma semana, testes com quatro questões de múltipla escolha a cinco alunos. Os resultados foram representados na matriz.

[tex]\qquad \begin{bmatrix}
3 & 2 & 0 & 1 & 2 \\
3 & 2 & 4 & 1 & 2 \\
2 & 2 & 2 & 3 & 2 \\
3 & 2 & 4 & 1 & 0 \\
0 & 2 & 0 & 4 & 4
\end{bmatrix}
[/tex]

Nessa matriz os elementos das linhas de [tex]1[/tex] a [tex]5[/tex] representam as quantidades de questões acertadas pelos alunos Ana, Bruno, Carlos, Denis e Érica, respectivamente, enquanto que as colunas de [tex]1[/tex] a [tex]5[/tex] indicam os dias da semana, de segunda-feira a sexta-feira, respectivamente, em que os testes foram aplicados. O teste que apresentou maior quantidade de acertos foi o aplicado na

a) segunda-feira.
b) terça-feira.
c) quarta-feira.
d) quinta-feira.
e) sexta-feira.

3. (Enem 2018) A Transferência Eletrônica Disponível (TED) é uma transação financeira de valores entre diferentes bancos. Um economista decide analisar os valores enviados por meio de TEDs entre cinco bancos [tex](1, 2, 3, 4[/tex] e [tex]5[/tex]) durante um mês. Para isso, ele dispõe esses valores em uma matriz [tex]A=(a_{ij})[/tex], em que [tex]1 \leq i \leq 5[/tex] e [tex]1 \leq j \leq 5[/tex], e o elemento [tex]a_{ij}[/tex] corresponde ao total proveniente das operações feitas via TED, em milhão de real, transferidos do banco [tex]i[/tex] para o banco [tex]j[/tex] durante o mês. Observe que os elementos [tex]a_{ii}=0[/tex], uma vez que TED é uma transferência entre bancos distintos. Esta é a matriz obtida para essa análise:

[tex]\qquad A=\begin{bmatrix}
0 & 2 & 0 & 2 & 2 \\
0 & 0 & 2 & 1 & 0 \\
1 & 2 & 0 & 1 & 1 \\
0 & 2 & 2 & 0 & 0 \\
3 & 0 & 1 & 1 & 0
\end{bmatrix}
[/tex]

Com base nessas informações, o banco que transferiu a maior quantia via TED é o banco

a) [tex]1.[/tex]
b) [tex]2.[/tex]
c) [tex]3.[/tex]
d) [tex]4.[/tex]
e) [tex]5.[/tex]

4. (Enem 2012) Um aluno registrou as notas bimestrais de algumas de suas disciplinas numa tabela. Ele observou que as entradas numéricas da tabela formavam uma matriz [tex]4 \times 4[/tex], e que poderia calcular as médias anuais dessas disciplinas usando produto de matrizes. Todas as provas possuíam o mesmo peso, e a tabela que ele conseguiu é mostrada a seguir.

[tex]\qquad \begin{array}{|c|c|c|c|c|}
\hline
\textbf{Disciplina} & \textbf{Bimestre 1} & \textbf{Bimestre 2} & \textbf{Bimestre 3} & \textbf{Bimestre 4} \\ \hline
Matemática & 5,9 & 6,2 & 4,5 & 5,5 \\ \hline
Português & 6,6 & 7,1 & 6,5 & 8,4 \\ \hline
Geografia & 8,6 & 6,8 & 7,8 & 9,0 \\ \hline
História & 6,2 & 5,6 & 5,9 & 7,7 \\ \hline
\end{array}[/tex]

Para obter essas médias, ele multiplicou a matriz obtida a partir da tabela por

a)[tex]\begin{bmatrix}
\dfrac{1}{2} & \dfrac{1}{2} & \dfrac{1}{2} & \dfrac{1}{2}\\
\end{bmatrix}
[/tex]

b) [tex]\begin{bmatrix}
\dfrac{1}{4} & \dfrac{1}{4} & \dfrac{1}{4} & \dfrac{1}{4}\\
\end{bmatrix}
[/tex]

c) [tex]\begin{bmatrix}
1\\
1\\
1\\
1
\end{bmatrix}
[/tex]

d) [tex]\begin{bmatrix}
\dfrac{1}{2}\\
\dfrac{1}{2}\\
\dfrac{1}{2}\\
\dfrac{1}{2}
\end{bmatrix}
[/tex]

e) [tex]\begin{bmatrix}
\dfrac{1}{4}\\
\dfrac{1}{4}\\
\dfrac{1}{4}\\
\dfrac{1}{4}
\end{bmatrix}
[/tex]

5. (Enem 2023) Os candidatos A, B e C participaram de um concurso composto por uma prova de Matemática, uma de Português e outra de Geografia, sendo os pesos dessas três provas diferentes. As notas obtidas por esses três candidatos e os pesos atribuídos a essas provas estão representados nas tabelas:

[tex]\textbf{Tabela I (Notas)}[/tex]

[tex]\begin{array}{|c|c|c|c|}
\hline
\textbf{Candidato} & \textbf{Matemática} & \textbf{Português} & \textbf{Geografia} \\ \hline
A & 9 & 6 & 7 \\ \hline
B & 8 & 7 & 8 \\ \hline
C & 9 & 5 & 6 \\ \hline
\end{array}[/tex]

[tex]\textbf{Tabela II (Pesos)}[/tex]

[tex]\begin{array}{|c|c|}
\hline
\textbf{Matérias} & \textbf{Pesos} \\ \hline
\text{Matemática} & 3 \\ \hline
\text{Português} & 2 \\ \hline
\text{Geografia} & 1 \\ \hline
\end{array}[/tex]

As notas finais são obtidas somando-se os produtos das notas pelos respectivos pesos. As notas finais dos três candidatos podem ser obtidas multiplicando-se a matriz das notas dos três candidatos nas três provas pela matriz dos pesos das três provas. A matriz das notas finais dos três candidatos é

a)[tex]\begin{bmatrix}
52 & 37 & 43\\
\end{bmatrix}
[/tex]

b) [tex]\begin{bmatrix}
46\\
46\\
43\\
\end{bmatrix}
[/tex]

c) [tex]\begin{bmatrix}
66\\
46\\
20\\
\end{bmatrix}
[/tex]

d) [tex]\begin{bmatrix}
27 & 12 & 7\\
24 & 14 & 8\\
27 & 10 & 6\\
\end{bmatrix}
[/tex]

e) [tex]\begin{bmatrix}
27 & 18 & 21\\
16 & 14 & 16\\
9 & 5 & 6\\
\end{bmatrix}
[/tex]

6. Construir a matriz [tex]A=(a_{ij})_{3 \times 3}[/tex] tal que [tex]a_{ij}=i-j[/tex].

7. Dadas as matrizes [tex]A=\begin{bmatrix}
1 & 5 & 7\\
3 & 9 & 11
\end{bmatrix}
[/tex], [tex]B=\begin{bmatrix}
2 & 4 & 6\\
8 & 10 & 12
\end{bmatrix}
[/tex] e [tex]\begin{bmatrix}
0 & -1 & -5\\
1 & 4 & 7
\end{bmatrix}
[/tex], calcule [tex]A+B+C[/tex], [tex]A-B+C[/tex], [tex]A-B-C[/tex], [tex]-A+B-C[/tex].

8. Resolva a equação matricial [tex]\begin{bmatrix}
a & b\\
c & d
\end{bmatrix}
\cdot
\begin{bmatrix}
3 & 1\\
-2 & 2
\end{bmatrix}
=
\begin{bmatrix}
5 & 7\\
-5 & 9
\end{bmatrix}
[/tex].

9. Prove que, se [tex]A[/tex] e [tex]B[/tex] são matrizes comutáveis, vale a igualdade: [tex](A+B) \cdot (A-B)=A^2-B^2[/tex].

10. Determine [tex]x, y, z[/tex] para que a matriz [tex]\begin{bmatrix}
1 & x & 5 \\
2 & 7 & -4\\
y & z & -3
\end{bmatrix}
[/tex] seja simétrica.

11. Determine [tex]x, y, z[/tex] para que a matriz [tex]\begin{bmatrix}
0 & -4 & 2 \\
x & 0 & 1-z\\
y & 2z & 0
\end{bmatrix}
[/tex] seja antissimétrica.

12. Prove que, se [tex]A[/tex] e [tex]B[/tex] são matrizes inversíveis de ordem [tex]n[/tex], então [tex](A \cdot B)^{-1}=B^{-1} \cdot A^{-1}[/tex].

13. (Fatec-SP) Sejam a matriz [tex]A=\begin{pmatrix}
3 & -1 \\
x & y
\end{pmatrix}
[/tex], em que [tex]x[/tex] e [tex]y[/tex] são números reais, e [tex]I_2[/tex] a matriz identidade de ordem [tex]2[/tex]. Se [tex]A^2=I_2[/tex], então o valor do módulo de [tex]x \cdot y[/tex] é

a) [tex]0[/tex].
b) [tex]8[/tex].
c) [tex]10[/tex].
d) [tex]16[/tex].
e) [tex]24[/tex].

14. Considerando as matrizes [tex]M_1=\begin{pmatrix}
0 & 1 \\
1 & 1
\end{pmatrix}[/tex], [tex] M_2=M_1 \cdot M_1, M_3=M_2 \cdot M_1, \cdots, M_n=M_{n-1} \cdot M_1[/tex], o número situado na segunda linha e segunda coluna da matriz [tex]M_{10}[/tex] é

a) [tex]56.[/tex]
b) [tex]67.[/tex]
c) [tex]78.[/tex]
d) [tex]89.[/tex]

[tex]15.[/tex] (FGV-SP) Sendo [tex]A=\begin{pmatrix}
1 & 1 \\
0 & 1
\end{pmatrix}[/tex] e [tex]B=\begin{pmatrix}
170 \\
10
\end{pmatrix}[/tex], a matriz [tex]X=\begin{pmatrix}
x \\
y
\end{pmatrix}[/tex] na equação [tex]A^{16} \cdot X=B[/tex] será

a) [tex]\begin{pmatrix}
5 \\
5
\end{pmatrix}[/tex]

b) [tex]\begin{pmatrix}
0 \\
10
\end{pmatrix}[/tex]

c) [tex]\begin{pmatrix}
10 \\
5
\end{pmatrix}[/tex]

d) [tex]\begin{pmatrix}
10 \\
10
\end{pmatrix}[/tex]

e) [tex]\begin{pmatrix}
5 \\
10
\end{pmatrix}[/tex]

Equipe COM – OBMEP