✏ Link da Sala para dispositivos da Apple.
Um passeio pelo mundo da Equação Quadrática
Na maioria das vezes, quando alguém vai aprender algo, uma pergunta que surge quase que naturalmente é:
– Onde eu vou usar isso?
Assim, muitos de vocês estão pensando com os seus respectivos botões:
– Equação quadrática . . . Qual a aplicação disso no dia a dia de uma pessoa?
Bom, com certeza não encontramos equações quadráticas dentro do sapato que a gente vai calçar. Também não vamos vê-las quando formos pegar a pasta e a escova de dentes dentro do armário do banheiro. Muito menos em cima da mesa, junto com o nosso café da manhã!
Lembre-se sempre de que não usar uma ferramenta matemática no seu cotidiano não é sinônimo de que essa ferramenta seja inútil.
O autor do projeto decidiu construir uma calçada pavimentada em torno da área a ser plantada, de modo que fiquem [tex]12[/tex] metros quadrados de terra para o cultivo das flores.
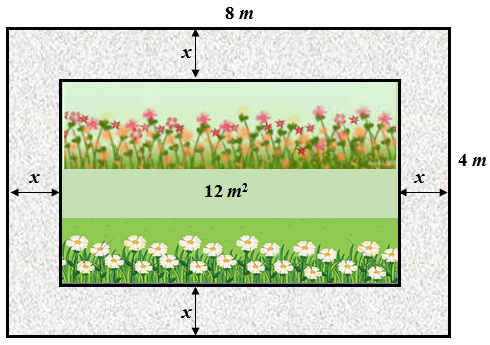
Para comprar o material, é claro que alguém precisará determinar a largura dessa calçada, não é?
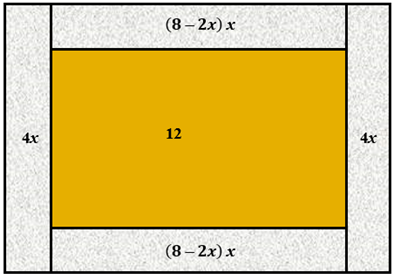
E para isso, observe que a área total de [tex]32 \text{ m}^2[/tex] destinada ao jardim pode ser decomposta em cinco áreas, de acordo com a figura ao lado. Portanto, considerando todas as medidas de área em [tex]\text{ m}^2[/tex], segue que:
[tex]\quad 32=\left(8-2x\right)\cdot x+\left(8-2x\right)\cdot x+4x+4x+12[/tex]
[tex]\quad 32=8x-2x^2+8x-2x^2+8x+12[/tex]
[tex]\quad 20=24x-4x^2[/tex]
[tex]\quad 4x^2-24x+20=0[/tex]
[tex]\quad \boxed{x^2-6x+5=0} \, .[/tex]
A igualdade obtida é um exemplo de equação quadrática.
Dito isso, como todos já perceberam, vamos estudar o objeto matemático denominado Equação Quadrática, ou Equação do 2º grau ou, mais sofisticadamente, Equação Polinomial do 2º grau. Uma ferramenta com inúmeras aplicações não no dia a dia da maioria das pessoas, mas em situações específicas do dia a dia de muita gente.
Esta é a primeira de três Salas que apresentaremos. No canto inferior direito de cada uma elas, vocês encontrarão links para ir para a próxima ou voltar para a anterior, se for o caso.
Bons estudos!
Um Pouco de História
Nesse início de conversa, não vamos definir formalmente o que é uma equação quadrática; isso será feito posteriormente. Só vamos lembrar que esse objeto é uma igualdade da forma [tex]ax^2+bx+c=0[/tex], na qual [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] são números reais quaisquer, com [tex]a \neq 0[/tex], e [tex]x[/tex] é um valor a ser determinado, se conhecermos [tex]a[/tex], [tex]b[/tex] e [tex]c.[/tex]
Vamos iniciar os nossos estudos usando a História para mostrar que problemas envolvendo, de alguma forma, a ideia de se resolver equações, não necessariamente quadráticas, estiveram presentes entre vários povos, desde muito tempo atrás.
Egito
Semelhantemente a muitos escritos de diversas outras nações, trechos da matemática egípcia foram encontrados em pedras. Mas também papiros resistiram ao desgaste do tempo por milhares de anos e contribuíram positivamente para a descoberta dos estudos matemáticos de origem egípcia.
Um importante documento egípcio é o papiro de Rhind, que data de 1650 a.C. e mede cerca de 30 cm de largura e 5 m de comprimento. Este artefato está localizado no British Museum (exceto alguns fragmentos localizados no Brooklyn Museum) e é também conhecido como Papiro de Ahmes, em homenagem ao escriba que o copiou.
 The Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus
Imagem extraída de The British Museum.
É possível encontrar neste papiro diversos problemas que hoje classificamos como aritméticos ou algébricos. Dentre os algébricos, há a abordagem de soluções de equações lineares que atualmente são escritas na forma [tex]x+ax=b[/tex] ou [tex]x+ax+bx=c[/tex], com [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] números conhecidos, e [tex]x[/tex] a incógnita.
No papiro, há a abordagem do método da Falsa Posição na resolução de tais equações. Vejamos um exemplo.
“Uma quantidade e o seu quarto torna-se 15. Qual é esta quantidade?”
Usando a notação algébrica atual, a solução poderia ser assim registrada:
1º passo: Chamemos de [tex]x[/tex] a quantidade procurada. Daí podemos escrever
[tex]\qquad x+ \dfrac{x}{4}=15\\
\qquad x \cdot \left(1+ \dfrac{1}{4} \right)=15.[/tex]
2º passo: Com a finalidade de eliminar a fração dessa equação, vamos substituir [tex]x[/tex] por [tex]4[/tex] na expressão [tex]x+ \dfrac{x}{4}[/tex], supondo ser essa uma solução.
[tex]\qquad 4 \cdot \left(1+ \dfrac{1}{4} \right)=5.[/tex]
Verificamos que [tex]x=4[/tex] não é solução da equação. Agora, a ideia é encontrar uma constante que multiplicada por [tex]5[/tex] chegue à solução.
3º passo: Dividindo a constante [tex]15[/tex] (proveniente do passo [tex]1[/tex]) por [tex]5[/tex] (proveniente do passo [tex]2[/tex]), obtemos o resultado [tex]3[/tex].
Agora, multiplicando a expressão obtida no passo [tex]2[/tex] por esse resultado, segue que:
[tex]\qquad 3 \cdot 4 \cdot \left(1+ \dfrac{1}{4} \right)=3 \cdot 5=15.[/tex]
Finalmente, conclui-se que a solução do problema utilizando o método da Falsa Posição é [tex]\boxed{x=3 \times 4 = 12}.[/tex]
Poucos são os registros de equações de segundo grau entre os egípcios, mas um papiro que data de aproximadamente [tex]1950[/tex] a.C., encontrado em Kahun, contém o seguinte problema:
“Uma dada superfície de [tex]100[/tex] unidades de área deve ser representada como a soma de dois quadrados cujos lados estão entre si como [tex]1: \dfrac{3}{4}[/tex].”
Neste documento, aparece pela primeira vez a solução de uma equação do [tex]2^\circ[/tex] grau. Atualmente, podemos enunciar este problema como mostrado abaixo:
“A soma das áreas de dois quadrados é [tex]100[/tex] unidades. O triplo do lado de um deles é igual ao quádruplo do lado do outro.”
Como modelar matematicamente tal situação? Vejamos.
Sejam [tex]x[/tex] e [tex]y[/tex] as medidas dos lados desses quadrados. Assim:
[tex]\qquad x^2+y^2=100 \qquad \qquad \textcolor{#0faaff}{(1)}[/tex]
[tex]\qquad 3x=4y. \qquad \qquad \qquad ~\textcolor{#20b0ff}{(2)}[/tex]
Vamos ver como se resolve esse sistema de equações utilizando o método da Falsa Posição?
1º passo: Suponhamos que [tex]x=4[/tex], então segue de [tex]\textcolor{#20b0ff}{(2)}[/tex] que [tex]y=3.[/tex]
2º passo: Assim, substituindo em [tex]\textcolor{#20b0ff}{(1)}[/tex], encontramos [tex]4^2+3^2=25.[/tex]
Observe que o par ordenado [tex](4, 3)[/tex] não é solução do problema em questão.
3º passo: Entretanto, multiplicando os dois membros da expressão [tex]4^2+3^2=25[/tex] por [tex]4[/tex], temos:
[tex]\qquad 4 \cdot (4^2+3^2)=4 \cdot 25 \\
\qquad 4 \cdot 3^2 +4 \cdot 4^2 = 100.[/tex]
4º passo: Como [tex]4 = 2^2[/tex], temos:
[tex]\qquad 2^2 \cdot 3^2+2^2 \cdot 4^2=100[/tex]
[tex]\qquad (2 \cdot 3)^2+(2 \cdot 4)^2=100[/tex]
[tex]\qquad 6^2+8^2=100[/tex].
Assim, obtemos que [tex]\boxed{x=6}~[/tex] e [tex]~\boxed{y=8}~[/tex] é solução do problema.
Mesopotâmia
O período em torno de [tex]4\ 000[/tex] a.C. foi marcado por certo progresso cultural pelo uso da escrita, da roda e dos metais. Na Mesopotâmia (região entre os rios Tigre e Eufrates), a civilização dos sumérios foi responsável pela construção de casas e templos decorados com cerâmicas e mosaicos artísticos em desenhos geométricos. Mas um avanço cultural grandioso foi o desenvolvimento da escrita cuneiforme, produzida com um estilete em tabuletas de barro cozidas pelo sol ou em fornos.
 Barra de argila. Antigo texto matemático babilônico sobre equações de segundo grau
Barra de argila. Antigo texto matemático babilônico sobre equações de segundo grau
Imagem extraída de The British Museum.
Os babilônios também foram uma das civilizações marcantes que ocuparam a região mesopotâmica. Na Babilônia, uma das primeiras aparições das equações quadráticas pode ser encontrada no clássico problema mostrado a seguir.
“Pede-se o lado de um quadrado sabendo que a diferença entre a área desse quadrado e seu lado é o número [tex]870[/tex].”
Nos dias de hoje, observamos que esse problema deve ser pensado apenas numericamente, uma vez que não podemos extrair um comprimento de uma área.
Feita a ressalva, algebricamente, o problema pode ser modelado como [tex]x^2-x=870[/tex],
O procedimento realizado pelos escribas nas tabuletas de argila corresponde à seguinte sequência de cálculos:
[tex]1^\circ)[/tex] Tome a metade de [tex]1[/tex] (coeficiente de [tex]x^2[/tex]): [tex]1/2=0,5.[/tex]
[tex]2^\circ)[/tex] Multiplique por ela mesma: [tex]0,5 \times 0,5 = 0,25.[/tex]
[tex]3^\circ)[/tex] Some o resultado a [tex]870[/tex]: [tex]870+0,25=870,25.[/tex]
[tex]4^\circ)[/tex] Obtém-se um quadrado: [tex]870,25=29,5^2.[/tex]
[tex]5^\circ)[/tex] Tomando a metade de [tex]1[/tex] e somando à base [tex]29,5[/tex], obtém-se [tex]30[/tex], que é o lado do quadrado procurado.
Utilizando métodos atuais, esse procedimento é justificado pelo que conhecemos como o Complemento de Quadrados. Observe.
Vamos tentar converter o lado esquerdo da equação [tex]x^2-x=870[/tex] no produto notável conhecido como Quadrado da Diferença de Dois Termos, ou seja, uma expressão da forma [tex](x-a)^2=x^2-2\cdot a\cdot x+a^2[/tex].
[tex]1^\circ)[/tex] Veja que [tex]x^2-x=x^2-x+\dfrac{1}{4}-\dfrac{1}{4}.[/tex]
[tex]2^\circ)[/tex] Reescrevamos a expressão obtida da seguinte forma:
[tex]\qquad x^2-x=\left(x^2-2 \cdot x \cdot \dfrac{1}{2}+\dfrac{1}{4}\right) -\left(\dfrac{1}{2}\right)^2\\
\qquad x^2-x=\left(x-\dfrac{1}{2}\right)^2 -\left(\dfrac{1}{2}\right)^2\,.[/tex]
[tex]3^\circ)[/tex] Como [tex]x^2-x=870[/tex], segue que:
[tex]\qquad \left(x-\dfrac{1}{2}\right)^2 -\left(\dfrac{1}{2}\right)^2=870\\
\qquad \left(x-\dfrac{1}{2}\right)^2=870+0,25\\
\qquad \left(x-\dfrac{1}{2}\right)^2=870,25=(29,5)^2\,.[/tex]
[tex]4^\circ)[/tex] Desta forma, temos:
[tex]\qquad x-\dfrac{1}{2}=29,5\\
\qquad x=30[/tex]
ou
[tex]\qquad x-\dfrac{1}{2}=-29,5\\
\qquad x=-29.[/tex]
Por se tratar de uma medida de comprimento, apenas o valor [tex]x=30[/tex] é válido para o problema em questão.
Grécia
Os gregos foram a mais antiga civilização que desempenhou forte papel em relação ao formalismo matemático atual. Na Grécia, a natureza da matemática era mais abstrata, com mais aplicações práticas e muitas vezes com viés filosófico. Os gregos tomaram a matemática como ciência por meio do uso de demonstrações para validar resultados de argumentações.
Dentre tantos brilhantes matemáticos gregos que se destacaram, temos: Tales de Mileto, Pitágoras, Platão, Aristóteles, Parmênides, Zenon, Arquimedes, Apolônio, Ptolomeu, Diofanto, Euclides – com sua importante obra Os Elementos de Geometria – dentre outros.
O desenvolvimento da Geometria na Grécia proporcionou um grande desenvolvimento no tratamento geométrico de muitos problemas matemáticos: dentre eles, a equação quadrática.
Observemos um problema da obra Os Elementos.
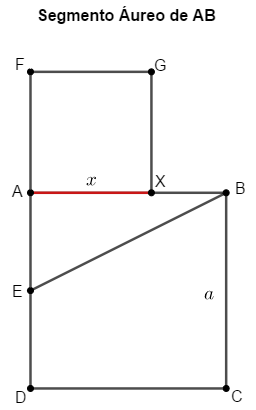
Proposição [tex]11[/tex] – Livro [tex]II[/tex] (Segmento Áureo):
“Dividir uma linha reta em duas partes tais que o retângulo contido pelo todo e uma das partes tenha área igual à área do quadrado sobre a outra parte.”
Podemos escrever esse texto como : “Dado um segmento de reta [tex]\overline{AB}[/tex], deve-se determinar o ponto [tex]X[/tex] desse segmento tal que o retângulo de lados [tex]\overline{AB}[/tex] e [tex]\overline{XB}[/tex] tenha a mesma área do quadrado de lado [tex]\overline{AX}[/tex]”.
Vamos modelar essa situação matematicamente:
[tex]1^\circ)[/tex] Indiquemos as medidas dos segmentos [tex]\overline{AB}~[/tex] e [tex]\overline{AX}~[/tex] por [tex]a[/tex] e [tex]x[/tex], respectivamente. Assim, [tex]a[/tex] e [tex]x[/tex] devem satisfazer à equação [tex]a \cdot (a-x)=x^2.[/tex]
[tex]2^\circ)[/tex] Construamos o quadrado [tex]ABCD[/tex] sobre o segmento dado [tex]\overline{AB}.[/tex]
[tex]3^\circ)[/tex] Tomemos o ponto médio [tex]E[/tex] do segmento [tex]\overline{DA}.[/tex]
[tex]4^\circ)[/tex] Tomemos [tex]F[/tex] sobre o prolongamento de [tex]\overline{DA}[/tex] de maneira que [tex]EF=EB.[/tex]
[tex]5^\circ)[/tex] Construamos um quadrado de lado [tex]\overline{AF}[/tex] externo ao quadrado [tex]ABCD.[/tex]
[tex]6^\circ)[/tex] O vértice [tex]X[/tex] desse quadrado, pertencente ao segmento [tex]\overline{AB}~[/tex], é a solução do problema.
Observe a figura abaixo à esquerda que apresenta com mais detalhes a construção geométrica realizada. A figura à direita mostra o “retângulo contido pelo todo e uma das partes” e o “quadrado sobre a outra parte” que têm a mesma área.
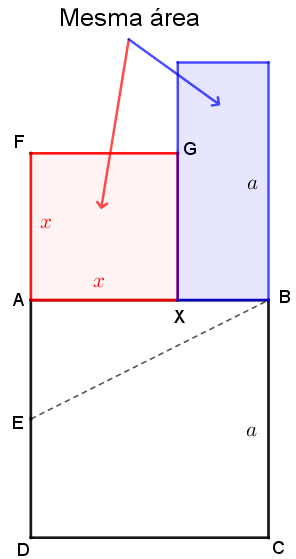
Algebricamente, sendo [tex]E[/tex] o ponto médio de [tex]\overline{AD}[/tex], então [tex]AE=\dfrac{1}{2}AD=\dfrac{a}{2}[/tex].
Aplicando o Teorema de Pitágoras no triângulo [tex]ABE[/tex], temos:
[tex]\qquad EB=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a \sqrt{5}}{2}[/tex].
Sendo [tex]AX=AF=x[/tex], por construção tem-se que:
[tex]\quad AF=EF-EA=EB-EA=\dfrac{a \sqrt{5}}{2}-\dfrac{a}{2}=\dfrac{a \cdot (\sqrt{5}-1)}{2}[/tex].
O resultado encontrado corresponde à raiz positiva da equação [tex]a \cdot (a-x)=x^2[/tex], e é a medida do segmento [tex]\overline{AX}.[/tex]
Índia
Matemáticos indianos também deram importantes contribuições para o desenvolvimento da Matemática. A contribuição mais significativa da Índia foi o sistema de numeração decimal e posicional, com o uso de nove símbolos e do zero.
Dentre os grandes matemáticos indianos, temos Aryabhata (século VI D.C.), Brahmagupta (século VII D.C.), Sridhara (século XI D.C) e, o mais famoso deles, Bhaskara (1114-1185).
Bhaskara foi o mais importante matemático do século XII. Ele preencheu as lacunas deixadas na obra de Brahmagupta, apresentando uma solução para a equação geral [tex]x^2=1+py^2[/tex] e considerando o problema da divisão por zero.
As obras mais conhecidas de Bhaskara são o Lilavati e o Vija-Ganita que contêm problemas sobre os tópicos favoritos dos Hindus: equações lineares e quadráticas, mensuração, progressões aritméticas e geométricas, tríades pitagóricas, entre outros.
Apesar de todo seu talento, Bhaskara não foi o matemático que deu o passo fundamental para o desenvolvimento das equações quadráticas. A regra que usava e que originou a fórmula atual que muitos chamam de “fórmula de Bhaskara” foi devida a Sridhara.
A imagem a seguir mostra como Brahmagupta e seus contemporâneos escreviam, respectivamente, as equações [tex]x^2-10x=-9~[/tex] e [tex]~7xy+\sqrt{12}-8=3x^2+10x.[/tex] (O primeiro membro da equação era escrito em uma linha e o segundo membro na linha abaixo.)
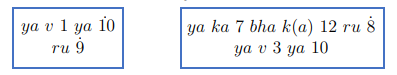
Ficou curioso(a)?
Use a tabelinha abaixo para tentar traduzir.

Arábia
A civilização arábica influenciou fortemente o desenvolvimento da matemática transformando suas cidades em grandes centros de saber.
Bagdá foi uma cidade que passou a ser a capital oriental do conhecimento e produção científica. Ali fora fundada a biblioteca que ficou conhecida como Casa da Sabedoria, que inicialmente se ocupou de traduções para o árabe de textos persas, hindus e gregos. Com o tempo, tornou-se uma instituição de pesquisa e produção científica de grande destaque no período entre os séculos IX e XIII.
Um estudioso de grande importância vinculado à casa da sabedoria foi o matemático e astrônomo Muhammad Ibn Musa Al-Khwarizmi (780-850), que influenciou significativamente os rumos da matemática. Duas obras dele merecem destaque:
- O “Livro da Adição e da Subtração segundo o Cálculo dos Indianos”, no qual são abordados temas sobre o sistema de numeração decimal hindu e suas operações.
- O “Tratado sobre Cálculo da Al-Jabr e Al-Muqabalah”, considerado o alicerce da álgebra como área de conhecimento matemático. Na obra, o autor descreve soluções de equações de primeiro e segundo graus.
Observe, no quadro abaixo, o procedimento realizado por al-Khwarizmi (ou al-Khowarizmi, ou ainda Alcuarismi) para a solução da equação quadrática [tex]x^2+10x=39[/tex].
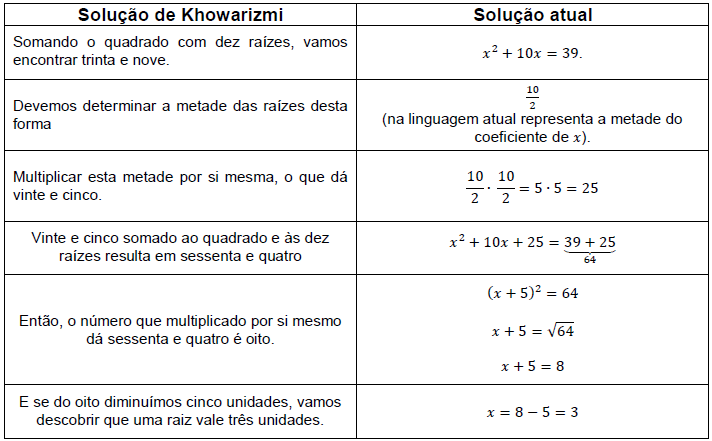 Imagem extraída de Guelli, 1995, p. 29.
Imagem extraída de Guelli, 1995, p. 29.
É importante notar que na passagem de [tex](x+5)^2=64[/tex] para [tex] x+5=\sqrt{64}[/tex] foi considerada apenas a raiz positiva. Porém, hoje sabemos que há duas raízes reais dadas pelas igualdades [tex]x+5=\pm 8[/tex].
Nessa obra Al-Khowarizmi classificou as equações de primeiro e segundo graus em seis tipos canônicos, a saber:
Tipo 1: [tex]ax^2=bx[/tex] (quadrado igual a uma raiz);
Tipo 2: [tex]ax^2=c[/tex] (quadrado igual a um número);
Tipo 3: [tex]bx=c[/tex] (raiz igual a número);
Tipo 4: [tex]ax^2+bx=c[/tex] (quadrado e raiz igual a um número);
Tipo 5: [tex]ax^2+c=bx[/tex] (quadrado e número igual a uma raiz);
Tipo 6: [tex]bx+c=ax^2[/tex] (raiz e número igual a um quadrado).
Um fato curioso é que para Al-Khowarizmi a equação na forma [tex]ax^2+bx+c=0[/tex] não fazia sentido, pois ele não utilizava números negativos.
China
A civilização chinesa foi responsável por diversas inovações tecnológicas, tais como: o uso da impressão, da pólvora, do papel e da bússola.
Um dos textos matemáticos chineses que mais merecem destaque é o dos “Nove Capítulos sobre a Arte matemática”. O trabalho consta de [tex]246[/tex] problemas sobre agricultura, procedimentos em negócios, engenharia, agrimensura, resoluções de equações e propriedades de triângulos retângulos.
Um famoso matemático chinês foi Chu Shih-Chieh (1280-1303). Ele foi responsável por dois importantes tratados: Introdução ao Estudo da Matemática, em 1299, e O Precioso Espelho dos Quatro Elementos, em 1303, que é considerado a sua obra mais importante.
Em O Precioso Espelho dos Quatro Elementos, ele desenvolveu uma técnica diferenciada baseada na construção por aproximações sucessivas de raízes de equações de [tex]2^\circ[/tex] grau; tal técnica foi denominada método fan-fa; com ela era encontrava uma única raiz: a positiva.
Em 1819, o método fan-fa foi rebatizado para método de Horner em homenagem ao matemático inglês William George Horner, que desenvolveu o esquema de Horner para solução de equações algébricas e redescobriu o método fan-fa.
De lá para cá
Diversas outras culturas trabalharam no desenvolvimento de métodos de resolução da equação do [tex]2^\circ[/tex] grau. Mas a maneira de se resolver esse tipo de equação era basicamente como Bhaskara resolvia. O que aconteceu de novo foi, na realidade, o desenvolvimento da notação para representação dessas equações e diferentes formas para uma melhor representação de suas respectivas soluções.
Nessa caminhada, encontramos nomes como François Viète (1540-1603), René Descartes (1596-1650), matemáticos que podem ser encontrados na nossa Pequena Galeria de Grandes Matemáticos e sobre os quais voltaremos a falar na nossa próxima Sala.
Para finalizar esse breve histórico, percebam a evolução da notação algébrica de 1494 a 1693, observando as várias maneiras de representar a equação [tex]\boxed{x^2+5x-6=0}.[/tex]
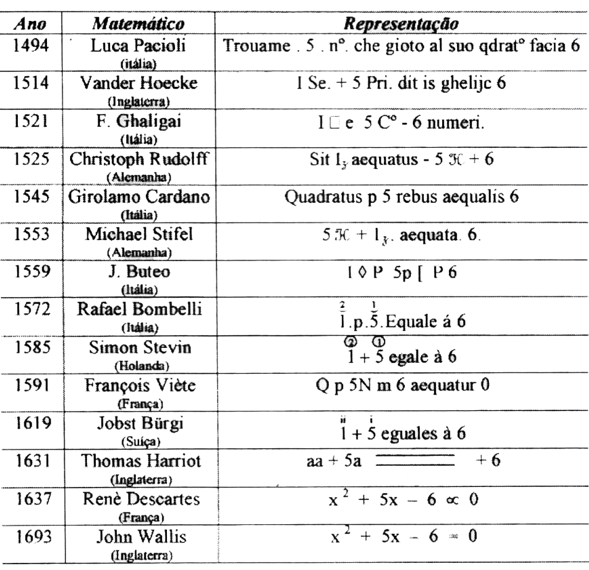 Imagem extraída de A Equação Quadrática – Alexandre Trovon
Imagem extraída de A Equação Quadrática – Alexandre Trovon
Um vídeo para aprender mais
Vídeoaula de História da Matemática do Mestrado PROFMAT
Professora Tatiana Roque
Equipe COM – OBMEP
Julho de 2023.
