Fórmula de Herão
✐ [tex]\boxed{A_t=\sqrt{p(p-a)(p-b)(p-c)}}[/tex],
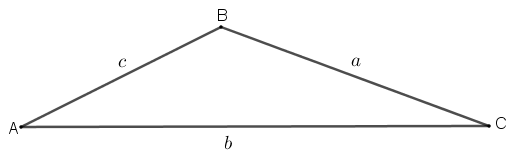
sendo [tex]a,\, b,\, c[/tex] os comprimentos dos lados e [tex]p=\dfrac{a+b+c}{2}[/tex] o semiperímetro do triângulo em questão.
Essa fórmula pode ser provada de diversas maneiras e, em qualquer uma delas, temos uma bela oportunidade de aprendermos mais um pouco de Matemática. E é isso que faremos:
- apresentaremos algumas belas demonstrações da Fórmula de Herão, cada uma com base em resultados interessantes de Matemática.
Nesta Sala Inicial, apresentaremos apenas um brevíssimo resumo das demonstrações. Para ter acesso a cada uma delas, basta clicar no botão correspondente.
Bons estudos, pessoal!
Dedução 1
A primeira dedução é uma das mais tradicionais e "usa e abusa" da Álgebra. Da Geometria propriamente dita são utilizados apenas dois resultados e dos mais conhecidos:
✐ Fórmula da área de um triângulo a partir de uma base e de sua respectiva altura:
[tex]\qquad \qquad \boxed{A_t=\dfrac{base \cdot altura}{2}}\, .[/tex]
✐ Teorema de Pitágoras: Em um triângulo retângulo de catetos com comprimentos [tex]c_1\, [/tex] e [tex]\, c_2[/tex] e hipotenusa com comprimento [tex]h[/tex], temos que:
[tex]\qquad \qquad \boxed{c_1^2+c_2^2=h^2}\, .[/tex]
Para conhecer esta demonstração, clique no botão abaixo.
Dedução 2
Esta segunda dedução é surpreendentemente curta, mas utiliza muita geometria elementar sobre triângulos e circunferências inscritas e dois resultados não muito conhecidos – o primeiro envolve apenas Geometria Euclidiana e o segundo, o menos conhecido, utiliza relações trigonométricas envolvendo tangentes e secantes de ângulos agudos:
✐ Lema 1: A área de um triângulo é igual ao produto da medida do raio da sua circunferência inscrita pelo seu semiperímetro.
✐ Lema 2: Se [tex]\alpha\, ,\, \beta\, ,\, \gamma[/tex] são medidas positivas de três ângulos tais que [tex]\alpha+\beta+\gamma=\dfrac{\pi}{2}[/tex], então:
[tex]\qquad \qquad \boxed{ \tan\,\alpha\cdot \tan\,\beta+ \tan\,\gamma \cdot \tan\,\alpha +\tan \gamma \, \cdot \tan\,\beta= 1}\, .[/tex]
Para ver as demonstrações da fórmula e dos Lemas,
clique no botão abaixo.
Dedução 3
Para a terceira demonstração da fórmula de Herão, além da famosa [tex]\dfrac{base \times altura}{2}[/tex] e de dois produtos notáveis, serão utilizados dois resultados tradicionais da trigonometria de um triângulo retângulo:
✐ Lei Fundamental da Trigonometria: Se [tex]\theta[/tex] é a medida de um dos ângulos internos de um triângulo, então:
[tex]\qquad \qquad \boxed{sen^2\,\theta +cos^2\,\theta=1}\, .[/tex]
✐ Lei dos Cossenos: Se [tex]a, b[/tex] e [tex]c[/tex] são os comprimentos dos lados de um triângulo qualquer e [tex]\theta[/tex] é a medida do ângulo definido pelos lados cujos comprimentos são [tex]a\, [/tex] e [tex]\, b[/tex], temos que:
[tex]\qquad \qquad \boxed{c^2=a^2+b^2-2ab\, cos\,\theta}\, .[/tex]
Para conhecer esta terceira demonstração, clique no botão abaixo.
Dedução 4
A quarta dedução da fórmula de Herão utiliza uma propriedade clássica sobre segmentos tangentes a uma circunferência e um dos Lemas da Dedução 2:
✐ Uma propriedade de tangência a circunferências: Se a partir de um ponto [tex]P[/tex] externo a uma circunferência [tex]\Gamma[/tex] traçarmos os segmentos [tex]\overline{PA}[/tex] e [tex]\overline{PB}[/tex] tangentes a [tex]\Gamma[/tex], com [tex]A[/tex] e [tex]B[/tex] pontos de [tex]\Gamma[/tex], então esses dois segmentos têm o mesmo comprimento.
✐ Lema: A área de um triângulo é igual ao produto da medida do raio da sua circunferência inscrita pelo seu semiperímetro.
Particularmente, para o Lema da Dedução 2, faremos uma segunda demonstração.
Trabalharemos também com conceitos e propriedades das
✐ circunferência inscrita e circunferência ex-inscrita a um dado triângulo. (Para relembrar esses conceitos, visite esta Sala de Leitura.)
Para acompanhar esta demonstração, clique no botão a seguir.
Dedução 5
O diferencial desta dedução é utilizar números complexos. Assim, serão utilizadas definições e propriedades básicas desse tipo de números. Nesta quinta dedução da fórmula de Herão, também serão utilizados um dos Lemas da Dedução 2 e a propriedade de tangência a circunferências da Dedução 4.
✐ Uma propriedade de tangência a circunferências: Se a partir de um ponto [tex]P[/tex] externo a uma circunferência [tex]\Gamma[/tex] traçarmos os segmentos [tex]\overline{PA}[/tex] e [tex]\overline{PB}[/tex] tangentes a [tex]\Gamma[/tex], com [tex]A[/tex] e [tex]B[/tex] pontos de [tex]\Gamma[/tex], então esses dois segmentos têm o mesmo comprimento.
✐ Lema: A área de um triângulo é igual ao produto da medida do raio da sua circunferência inscrita pelo seu semiperímetro.
Para acompanhar as demonstrações, clique no botão a seguir.
 |
Não disponibilizaremos problemas nesta Sala, pois o nosso objetivo é que vocês aprendam a Matemática envolvida nas demonstrações. |
Equipe COM – OBMEP
Julho de 2019.
