Circunferências ex-inscritas
|
Epa, o nome desta Sala não foi escrito erradamente? |
 |
 |
Não, o nome é esse mesmo! Leia o texto abaixo. |
Existem três tipos de circunferências notáveis associadas a um dado triângulo [tex]ABC[/tex]. Duas são mais conhecidas:
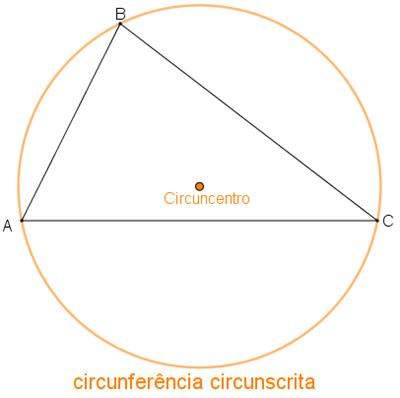
- A circunferência circunscrita ao triângulo [tex]ABC[/tex] é aquela que passa pelos seus três vértices. O centro dessa circunferência é denominado circuncentro e esse ponto é a interseção das mediatrizes dos lados do triângulo.
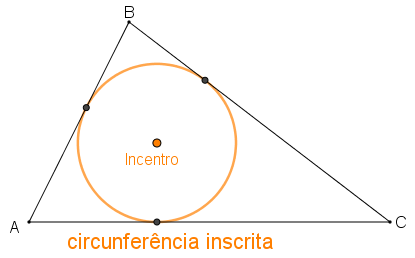
- A circunferência inscrita ao triângulo [tex]ABC[/tex] é aquela que está contida no interior desse triângulo e que é tangente aos seus três lados. O centro dessa circunferência é denominado incentro e esse ponto é a interseção das bissetrizes internas do triângulo.
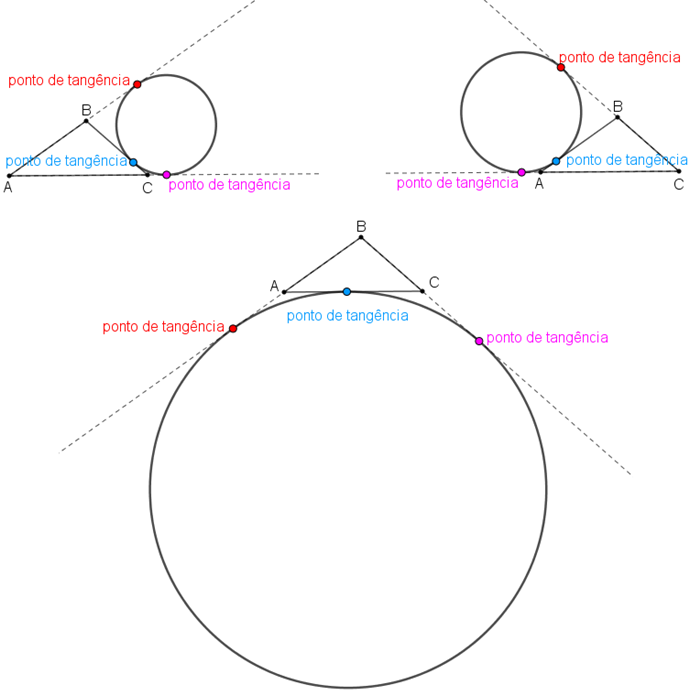
Aqui nesta Sala, vamos falar um pouco sobre o terceiro tipo de circunferência associada a um triângulo: circunferências ex-inscritas.
As ex-inscritas
Assim, dado um triângulo [tex]ABC[/tex], existem três circunferências ex-inscritas a ele:
- uma tangente ao lado [tex]BC[/tex] e aos prolongamentos dos lados [tex]AB[/tex] e [tex]AC \, [/tex];
- uma tangente ao lado [tex]AB[/tex] e aos prolongamentos dos lados [tex]CB[/tex] e [tex]CA \, [/tex];
- uma tangente ao lado [tex]CA[/tex] e aos prolongamentos dos lados [tex]BA[/tex] e [tex]BC \, [/tex].
É usual denotar cada um dos três ex-incentros de um triângulo utilizando a notação do respectivo vértice oposto ao lado ao qual a circunferência é tangente como índice e associar as circunferências ex-inscritas a esses vértices.
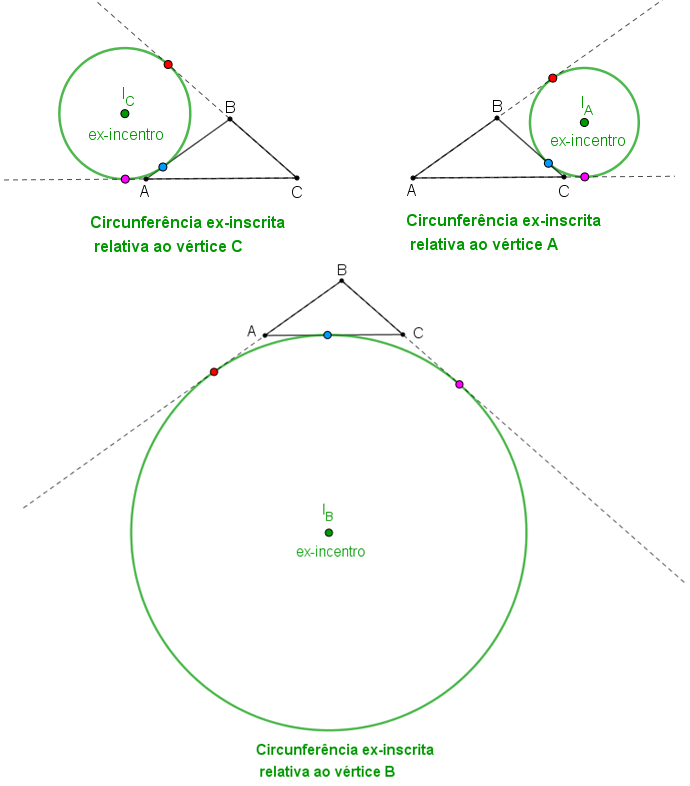
É comum também associar as três circunferências ex-inscritas aos respectivos lados do triângulo aos quais elas são tangentes. Assim, com relação às circunferências da figura acima:
- "a circunferência ex-inscrita relativa ao vértice [tex]C[/tex]" é também denominada "circunferência ex-inscrita ao lado [tex]AB[/tex]";
- "a circunferência ex-inscrita relativa ao vértice [tex]A[/tex]" é também denominada "circunferência ex-inscrita ao lado [tex]BC[/tex]";
- "a circunferência ex-inscrita relativa ao vértice [tex]B[/tex]" é também denominada "circunferência ex-inscrita ao lado [tex]CA[/tex]".
(1) Uma propriedade importante e que ajuda a traçar as circunferências ex-inscritas a um dado triângulo garante que:
- Dado um triângulo [tex]ABC[/tex], o centro da circunferência ex-inscrita tangente ao lado [tex]BC[/tex] e aos prolongamentos dos lados [tex]AB[/tex] e [tex]AC \, [/tex] é o ponto [tex]I_A[/tex] resultante da interseção da bissetriz interna relativa ao vértice [tex]A[/tex] e das bissetrizes externas relativas aos vértices [tex]B \, [/tex] e [tex] \, C.[/tex]
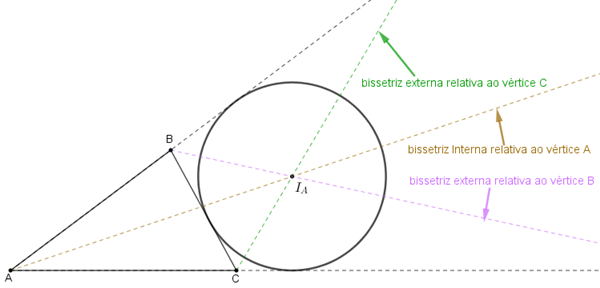
Para as outras duas circunferências ex-inscritas ao triângulo [tex]ABC[/tex], os respectivos ex-incentros são definidos de forma análoga.
(2) A próxima propriedade não é uma característica exclusiva das circunferências ex-inscritas a um triângulo, mas ajuda a traçá-las:
- Os raios definidos pelo centro de uma circunferência ex-inscrita e seus três pontos de tangência formam ângulos retos com os respectivos lados intersectados do triângulo (ou com os seus prolongamentos).
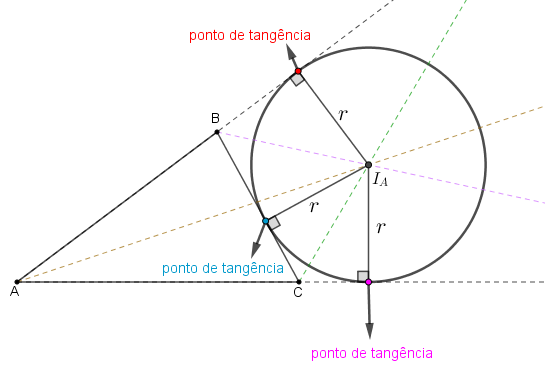
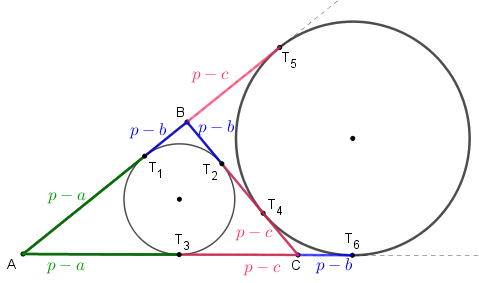
(3) Seja [tex]ABC[/tex] um triângulo cujos lados [tex]AB \, [/tex], [tex]BC \, [/tex] e [tex] \, CA[/tex] têm comprimentos [tex]c \, , \, a \, , b \, [/tex], respectivamente.
Se [tex]T_1 \, , \, T_2 \, , \, T_3 \, [/tex] são os pontos de tangência da circunferência inscrita ao triângulo [tex]ABC \, [/tex]; [tex]T_4 \, , \, T_5 \, , \, T_6 \, [/tex] são os pontos de tangência da circunferência ex-inscrita relativa ao vértice [tex]A[/tex] do triângulo [tex]ABC \, [/tex] e [tex]p=\dfrac{a+b+c}{2}[/tex] é o semiperímetro do triângulo [tex]ABC[/tex], então:
- Os comprimentos dos segmentos [tex]\textcolor{#009900}{AT_1} \, [/tex] e [tex] \, \textcolor{#009900}{AT_3}[/tex] são iguais a [tex]\textcolor{#009900}{p-a}.[/tex]
- Os comprimentos dos segmentos [tex]\textcolor{#0000FF}{BT_1} \, [/tex], [tex] \, \textcolor{#0000FF}{BT_2} \, [/tex] e [tex] \, \textcolor{#0000FF}{CT_6}[/tex] são iguais a [tex]\textcolor{#0000FF}{p-b}.[/tex]
- Os comprimentos dos segmentos [tex]\textcolor{#FF3366}{CT_2} \, [/tex], [tex] \, \textcolor{#FF3366}{CT_3} \, [/tex] e [tex] \, \textcolor{#FF3366}{BT_5}[/tex] são iguais a [tex]\textcolor{#FF3366}{p-c}.[/tex]
Usando as propriedades (1) e (2), podemos particularmente traçar as circunferências ex-inscritas a um dado triângulo. Então, utilizem um applet para obter a circunferência ex-inscrita tangente ao lado [tex]BC[/tex] de um dado triângulo [tex]ABC.[/tex] É só clicar no botão abaixo e seguir as instruções.
Bom proveito, pessoal!
As ex-inscritas e as inscritas
Consideremos o triângulo [tex]ABC[/tex] cujos lados [tex]AB \, [/tex], [tex]BC \, [/tex] e [tex] \, CA[/tex] têm comprimentos [tex]c \, , \, a \, , b \, [/tex], respectivamente.
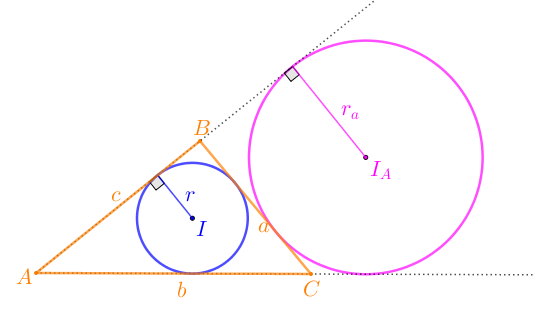
Vamos supor que [tex]r[/tex] é o raio da circunferência inscrita em [tex]ABC[/tex], [tex]r_a[/tex] é o raio da circunferência ex-inscrita ao lado [tex]BC[/tex] e [tex]p=\dfrac{a+b+c}{2}[/tex] é o semi perímetro de [tex]ABC[/tex].
A próxima figura ilustra propriedades gerais relativas a circunferências inscritas e ex-inscritas.
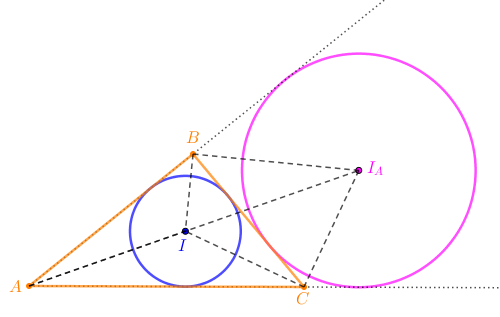
(4) O vértice [tex]A[/tex], o incentro [tex]I[/tex] e o ex-incentro [tex]I_A[/tex] são colineares.
- Esta propriedade é uma decorrência direta da definição do ex-incentro [tex]I_A[/tex], já que este é um ponto da bissetriz interna do vértice [tex]A.[/tex]
(5) A área [tex]S[/tex] do triângulo [tex]ABC[/tex] é dada pelo produto [tex]\boxed{p\cdot r} \, .[/tex]
- Se [tex]\textcolor{blue}{[AIB]}[/tex], [tex]\textcolor{blue}{[BIC]}[/tex] e [tex]\textcolor{blue}{[CIA]}[/tex] indicam as áreas dos respectivos triângulos indicados em cada notação, observe que:
[tex]\qquad S=\textcolor{blue}{[AIB]}+\textcolor{blue}{[BIC]}+\textcolor{blue}{[CIA]}\\
\qquad S=\dfrac{c\cdot r}{2}+\dfrac{a\cdot r}{2}+\dfrac{b\cdot r}{2}\\
\qquad S=\dfrac{c+b+a}{2} \cdot r\\
\qquad \boxed{S=p \cdot r} \, .[/tex]
(6) A área [tex]S[/tex] do triângulo [tex]ABC[/tex] é dada pelo produto [tex]\boxed{(p-a)\cdot r_a} \, .[/tex]
Se [tex]\textcolor{#FF00FF}{[AI_AB]}[/tex], [tex]\textcolor{#FF00FF}{[AI_AC]}[/tex] e [tex]\textcolor{#FF00FF}{[BI_AC]}[/tex] indicam as áreas dos respectivos triângulos indicados em cada notação, observe que:
[tex]\qquad S=\textcolor{#FF00FF}{[AI_AB]}+\textcolor{#FF00FF}{[AI_AC]}-\textcolor{#FF00FF}{[BI_AC]}\\
\qquad S=\dfrac{c\cdot r_a}{2}+\dfrac{b\cdot r_a}{2}-\dfrac{a\cdot r_a}{2}\\
\qquad S=\dfrac{c+b-a}{2} \cdot r_a\\
\qquad S=\dfrac{c+b-a+a-a}{2} \cdot r_a\\
\qquad S=\left(\dfrac{c+b+a}{2} -\dfrac{2a}{2}\right)\cdot r_a\\
\qquad\boxed{ S=(p-a) \cdot r_a} \, .[/tex]
De maneira análoga, obtemos as duas próximas propriedades.
(7) A área do triângulo [tex]ABC[/tex] é dada pelo produto [tex]\boxed{(p-b)\cdot r_b} \, .[/tex]
(8) A área do triângulo [tex]ABC[/tex] é dada pelo produto [tex]\boxed{(p-c)\cdot r_c} \, .[/tex]
(9) Relação entre os centros das circunferências inscrita e ex-inscritas:[tex]\boxed{\dfrac{1}{r_a}+\dfrac{1}{r_b}+\dfrac{1}{r_c}=\dfrac{1}{r}} \, .[/tex]
Pelas propriedade (5) , (6) , (7) e (8) temos que:
[tex]\qquad S=p \cdot r=(p-a) \cdot r_a =(p-b) \cdot r_b =(p-c) \cdot r_c [/tex]
assim, segue que:
[tex]\qquad \begin{align*}\boxed{\dfrac{1}{r_a}+\dfrac{1}{r_b}+\dfrac{1}{r_c}}&=\dfrac{p-a}{S}+\dfrac{p-b}{S}+\dfrac{p-c}{S}\\
&=\dfrac{1}{S} \left(p-a+p-b+p-c\right)\\
&=\dfrac{1}{S} \left(3p-(a+b+c)\right)\\
&=\dfrac{1}{S} \left(3p-2p\right)\\
&=\dfrac{p}{S}\\
&=\boxed{\dfrac{1}{r}}\\
\end{align*}[/tex]
 |
Existem outras propriedades interessantes sobre triângulos e suas circunferências. |
Equipe COM – OBMEP
Julho de 2019.
