Dedução 5
Nesta quinta dedução utilizaremos as definições e propriedades básicas dos números complexos e dois resultados da Geometria Plana: um resultado sobre tangência de retas e circunferência e um segundo que relaciona a área de um triângulo com o raio da sua circunferência inscrita e seu semiperímetro.
Na nossa discussão, os fatos elementares da Trigonometria e da Geometria Plana que utilizaremos serão apenas citados.
Ferramentas necessárias
O que vamos utilizar diretamente na dedução:
- definição algébrica de um número complexo;
- definição trigonométrica de um número complexo;
- produto de números complexos, via forma algébrica;
- produto de números complexos, via forma trigonométrica.
Se precisar, clique no botão a seguir para relembrar essas definições e propriedades.
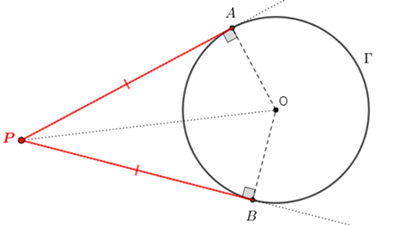
✐ Lema 1: Se, a partir de um ponto [tex]P[/tex] externo a uma circunferência [tex]\Gamma[/tex], traçarmos as retas [tex]PA[/tex] e [tex]PB[/tex] tangentes a [tex]\Gamma[/tex], com [tex]A[/tex] e [tex]B[/tex] pontos de [tex]\Gamma[/tex], então [tex]\overline{PA}[/tex] e [tex]\overline{PB}[/tex] terão o mesmo comprimento.
A dedução
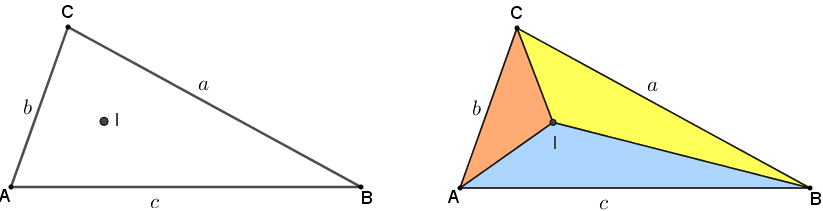
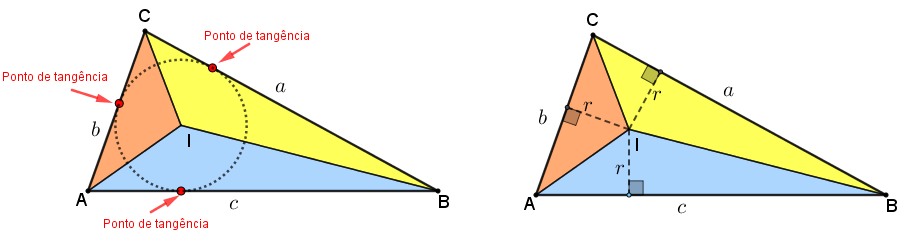
Sejam [tex]ABC[/tex] um triângulo e [tex]I[/tex] o centro da sua circunferência inscrita (incentro do triângulo [tex]ABC[/tex]). Considere que [tex]T_1[/tex], [tex]T_2[/tex] e [tex]T_3[/tex] são os pontos de tangência dos lados de [tex]ABC[/tex] com relação ao centro da sua circunferência inscrita.
Olhando [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] como pontos exteriores à circunferência inscrita do triângulo [tex]ABC[/tex], podemos utilizar o Lema 1 e concluir que:
- os segmentos [tex]\overline{AT_2}[/tex] e [tex]\overline{AT_3}[/tex] têm o mesmo comprimento, digamos [tex]x[/tex];
- os segmentos [tex]\overline{BT_1}[/tex] e [tex]\overline{BT_3}[/tex] têm o mesmo comprimento, digamos [tex]y[/tex];
- os segmentos [tex]\overline{CT_1}[/tex] e [tex]\overline{CT_2}[/tex] têm o mesmo comprimento, digamos [tex]z[/tex].
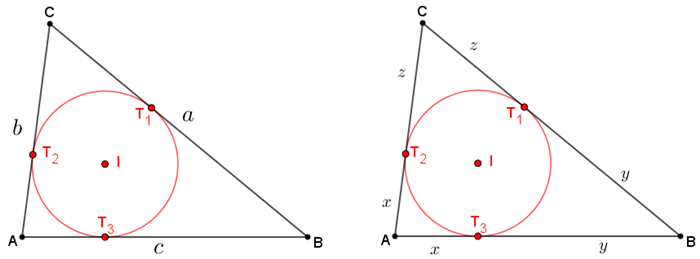
Com isso, temos que [tex]\boxed{a = y + z}[/tex] , [tex]\boxed{b = x + z}\, [/tex] e [tex]\, \boxed{c = x + y}\, .[/tex]
Vamos agora analisar três pares de triângulos internos ao triângulo [tex]ABC[/tex]: triângulos [tex]AT_2I[/tex] e [tex]AT_3I[/tex] ; triângulos [tex]BT_3I[/tex] e [tex]BT_1I[/tex] ; triângulos [tex]CT_1I[/tex] e [tex]CT_2I\, .[/tex]
Sendo [tex]r[/tex] a medida do raio da circunferência inscrita, observe que:
- Esses triângulos possuem um ângulo reto: os segmentos [tex]\overline{IT_1}[/tex], [tex]\overline{IT_2}[/tex] e [tex]\overline{IT_3}[/tex] são perpendiculares aos lados [tex]\overline{BC}[/tex], [tex]\overline{AC}[/tex] e [tex]\overline{AB}[/tex] respectivamente, uma vez que [tex]T_1[/tex], [tex]T_2[/tex] e [tex]T_3[/tex] são os pontos de tangência;
- os pares de triângulos "[tex]AT_2I[/tex] e [tex]AT_3I[/tex]", "[tex]BT_3I[/tex] e [tex]BT_1I[/tex]" e "[tex]CT_1I[/tex] e [tex]CT_2I\, [/tex]" possuem um lado comum;
- um dos catetos desses triângulos é raio da circunferência inscrita, cujo comprimento denotaremos por [tex]r[/tex].
Como "[tex]AT_2I[/tex] e [tex]AT_3I[/tex]", "[tex]BT_3I[/tex] e [tex]BT_1I[/tex]" e "[tex]CT_1I[/tex] e [tex]CT_2I\, [/tex]" são pares de triângulos retângulos com um cateto e a hipotenusa ordenadamente congruentes, então temos três pares de triângulos congruentes.

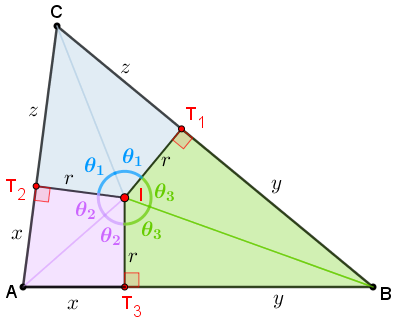
Dessa forma, podemos afirmar que:
- os ângulos [tex]T_1\hat IC[/tex] e [tex]T_2\hat IC[/tex] são congruentes;
- os ângulos [tex]T_2\hat IA[/tex] e [tex]T_3\hat IA[/tex] são congruentes;
- os ângulos [tex]T_1\hat IB[/tex] e [tex]T_3\hat IB[/tex] são congruentes.
Assim, se [tex]\theta_1[/tex], [tex]\theta_2[/tex] e [tex]\theta_3[/tex] forem as medidas desses ângulos, conforme mostra a figura ao lado, então podemos observar que [tex]2\theta_1+2\theta_2+2\theta_3=360^\circ[/tex], ou seja,
[tex]\boxed{\theta_1+\theta_2+\theta_3=180^\circ}.\qquad \textcolor{#800000}{(*)}[/tex]
A informação [tex]\textcolor{#800000}{(*)}[/tex] será muito útil no que se segue!
Agora vamos definir três números complexos:
[tex]\textcolor{#0099FF}{n_1=r + iz}\qquad;\qquad\textcolor{#CC66FF}{n_2=r + ix}\qquad;\qquad\textcolor{#66CC00}{n_3=r + iy}.\qquad \textcolor{#800000}{(ii)}[/tex]
Com base na figura acima, podemos representar geometricamente esse três números. Para isso, observe que [tex]\theta_1\lt 90^\circ[/tex], [tex]\theta_2\lt 90^\circ[/tex] e [tex]\theta_3\lt 90^\circ.[/tex]
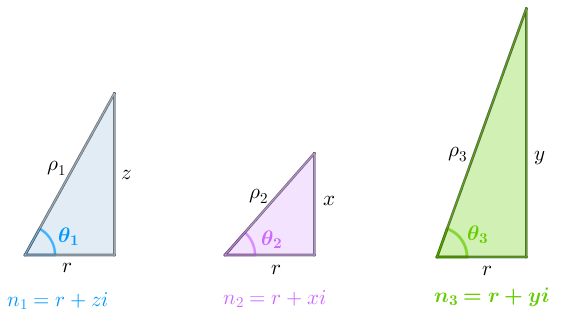
Com isso, temos a forma trigonométrica desses três números:
[tex]\textcolor{#0099FF}{n_1=\rho_1(cos\, \theta_1+isen\, \theta_1)}\qquad ;\qquad \textcolor{#CC66FF}{n_2=\rho_2(cos\, \theta_2+isen\, \theta_2)}\qquad ;\qquad \textcolor{#66CC00}{n_3=\rho_3(cos\, \theta_3+isen\, \theta_3)}.\qquad \textcolor{#800000}{(iii)}[/tex]
Vamos calcular o produto [tex]P[/tex] desses três números complexos, via suas formas trigonométricas:
[tex]\qquad P=n_1 \cdot n_2 \cdot n_3\\
\qquad P=(\rho_1(cos\, \theta_1+isen\, \theta_1)) \cdot (\rho_2(cos\, \theta_2+isen\, \theta_2)) \cdot (\rho_3(cos\, \theta_3+isen\, \theta_3))\\
\qquad P=\left[(\rho_1(cos\, \theta_1+isen\, \theta_1)) \cdot (\rho_2(cos\, \theta_2+isen\, \theta_2))\right] \cdot (\rho_3(cos\, \theta_3+isen\, \theta_3))\\
\qquad P=\rho_1\cdot \rho_2[cos\, (\theta_1+\theta_2)+isen\, (\theta_1+\theta_2)] \cdot (\rho_3(cos\, \theta_3+isen\, \theta_3))\\
\qquad P=\rho_1\cdot \rho_2\cdot \rho_3[cos\, \underbrace{(\theta_1+\theta_2+\theta_3)}_{180^\circ\text{, por }\textcolor{#800000}{(*)}}+isen\, \underbrace{(\theta_1+\theta_2+\theta_3)}_{180^\circ\text{, por }\textcolor{#800000}{(*)}}] \\
\qquad P=\rho_1\cdot \rho_2\cdot \rho_3[cos\, 180^\circ+isen\, 180^\circ] \\
\qquad P=\rho_1\cdot \rho_2\cdot \rho_3[(-1)+i(0)] \\
\qquad P=-\rho_1\cdot \rho_2\cdot \rho_3 .\\
[/tex]
Obtivemos como produto um número complexo com a parte imaginária igual a zero, ou seja, [tex]P[/tex] é um número real. Vamos obter agora o produto [tex]P[/tex] a partir da forma algébrica dos números [tex]n_1\, ,\, n_2\, ,\, n_3[/tex] e observar o que significa a parte imaginária de [tex]P[/tex] ser zero nessa forma:
[tex]\qquad P=n_1 \cdot n_2 \cdot n_3\\
\qquad P=(r + zi) \cdot (r + xi) \cdot (r + yi)\\
\qquad P=[(r + zi) \cdot (r + xi)] \cdot (r + yi)\\
\qquad P=[(r^2-z\cdot x)+(r\cdot x + z\cdot r)i] \cdot (r + yi)\\
\qquad P=[(r^2-z\cdot x) \cdot r-(r\cdot x + z\cdot r) \cdot y]+[(r^2-z\cdot x) \cdot y+(r\cdot x + z\cdot r)\cdot r]i\\
\qquad P=[(r^3-z\cdot x \cdot r) -(r\cdot x \cdot y + z\cdot r\cdot y)]+[(r^2 \cdot y-z\cdot x \cdot y)+(r^2 \cdot x + z\cdot r^2)]i\\
\qquad P=(r^3-z\cdot x \cdot r-r\cdot x \cdot y – z\cdot r\cdot y)+(r^2 \cdot y-z\cdot x \cdot y+r^2\cdot x + z\cdot r^2)i\, .\\
[/tex]
Sabemos que a parte imaginária de [tex]P[/tex] é zero; então, segue que:
[tex]\qquad r^2 \cdot y-z\cdot x \cdot y+r^2\cdot x + z\cdot r^2=0\\
\qquad r^2 \cdot y+r^2\cdot x + z\cdot r^2=z\cdot x \cdot y\\
\qquad r^2 \left( y+ x + z\right)=z\cdot x \cdot y\\
\qquad r^2 =\dfrac{x\cdot y \cdot z}{x+y+z},\\
[/tex]
e sendo [tex]r \gt 0[/tex], concluímos que [tex]r =\sqrt{\dfrac{x\cdot y \cdot z}{x+y+z}\, }.\qquad \textcolor{#800000}{(iv)}[/tex]
Agora, se denotarmos o semiperímetro do triângulo [tex]ABC[/tex] por [tex]p[/tex], então
[tex]\qquad p=\dfrac{a+b+c}{2}\\
\qquad p=\dfrac{(z+y)+(z+x)+(x+y)}{2}\\
\qquad p=\dfrac{2x+2y+2z}{2}\\
\qquad p=\dfrac{\cancel{2}(x+y+z)}{\cancel{2}}\\
\qquad p=x+y+z.\qquad \textcolor{#800000}{(v)}\\
[/tex]
Portanto, segue de [tex]\textcolor{#800000}{(iv)}[/tex] que [tex]r =\sqrt{\dfrac{x\cdot y \cdot z}{p}\, }.[/tex]
Dessa forma, pelo Lema 2, temos que a área [tex]A_t[/tex] do triângulo [tex]ABC[/tex] é dada por:
[tex]\qquad \qquad A_t =\sqrt{\dfrac{x\cdot y \cdot z}{p}\, } \, \cdot\, p\\[/tex]
donde
[tex]\qquad \qquad A_t =\dfrac {p}{\sqrt{p}} \cdot \sqrt{x\cdot y \cdot z\, }\, \, . \qquad \textcolor{#800000}{(vi)}[/tex]
Mas, de [tex]\textcolor{#800000}{(v)}[/tex], temos que [tex] p=x+y+z[/tex], então:
- [tex]x=(x+y+z)-y-z=p-(y+z)=p-a[/tex], ou seja, [tex]\boxed{x=p-a}[/tex];
- [tex]y=(x+y+z)-x-z=p-(x+z)=p-b[/tex], ou seja, [tex]\boxed{y=p-b}[/tex];
- [tex]z=(x+y+z)-x-y=p-(x+y)=p-c[/tex], ou seja, [tex]\boxed{z=p-c}[/tex].
Substituindo essas três igualdades obtidas em [tex]\textcolor{#800000}{(vi)}[/tex], obtemos:
[tex]\qquad A_t =\dfrac {p}{\sqrt{p}} \cdot \sqrt{(p-a)\cdot (p-b) \cdot (p-c)\, }\\
\qquad A_t= \sqrt{p}\cdot \sqrt{(p-a)\cdot (p-b) \cdot (p-c)\, } [/tex]
[tex]\qquad \, \fcolorbox{black}{#eee5de}{$A_t= \sqrt{p \cdot(p-a)\cdot (p-b) \cdot (p-c)}$}\, \\\, [/tex], que é a fórmula de Herão.
Equipe COM – OBMEP