Dedução 2
Esta dedução da fórmula de Herão utiliza dois resultados não muito conhecidos e algumas propriedades que envolvem triângulos e circunferências inscritas.
As justificativas para os dois Lemas podem ser feitas sem palavras, visualizando apenas imagens, e assim faremos. Mas se você não entender as justificativas visuais, deixaremos uma pequena explicação para cada imagem.
Os fatos elementares da Geometria Plana serão apenas citados.
Os lemas
✐ Lema 1: A área de um triângulo é igual ao produto da medida do raio da sua circunferência inscrita pelo seu semiperímetro.
A partir da figura abaixo não é difícil visualizar esse Lema.
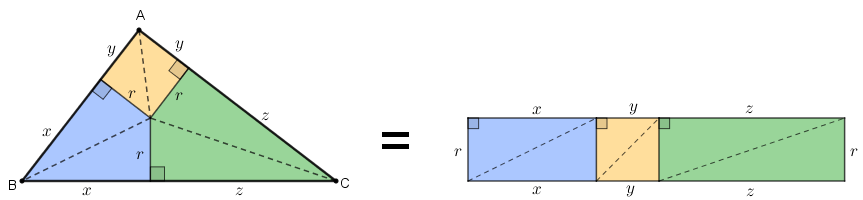
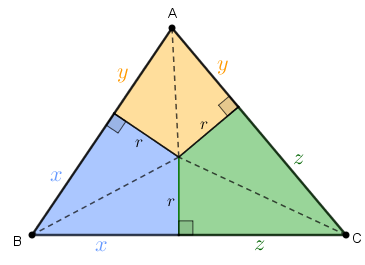
Com os triângulos internos ao triângulo [tex]ABC[/tex] já construídos, é simples explicar o resultado que chamamos de Lema 1, uma vez que o retângulo auxiliar desenhado à direita é construído a partir desses seis triângulos internos e, portanto, tem a mesma área de [tex]ABC[/tex].
Com efeito, se [tex]A_t[/tex] é a área do triângulo [tex]ABC[/tex], então [tex]\boxed{A_t=r\cdot(x+y+z)}[/tex].
Como o perímetro de [tex]ABC[/tex] é [tex]2x+2y+2z\, [/tex], então [tex]p=\dfrac{2x+2y+2z}{2}=x+y+z\, [/tex] é o semiperímetro; logo [tex]\fcolorbox{black}{#eee0e5}{$A_t=r\cdot p$}[/tex] e, assim, a área de um triângulo é o produto entre a medida do raio da sua circunferência inscrita e o seu semiperímetro.
Dessa forma, para justificar o Lema, basta justificar a construção dos triângulos internos ao triângulo [tex]ABC[/tex], com as medidas exibidas na figura.
Antes de ver as justificativas,
você pode utilizar um applet para simular o resultado.
É só clicar no próximo botão!
Applet
Depois de utilizar o applet, não se esqueça de fechar a janela que se abriu.
Se você ainda não conseguiu justificar a construção
dos seis triângulos internos, clique no próximo botão.
✐ Lema 2: Se [tex]\, \alpha\, ,\, \beta\, ,\, \gamma\, [/tex] são medidas positivas de três ângulos tais que [tex]\alpha+\beta+\gamma=\dfrac{\pi}{2}[/tex], então:
[tex]\qquad \qquad \boxed{ \tan\,\alpha\cdot \tan\,\beta+ \tan\,\gamma \cdot \tan\,\alpha +\tan \gamma \, \cdot \tan\,\beta= 1}\, .[/tex]
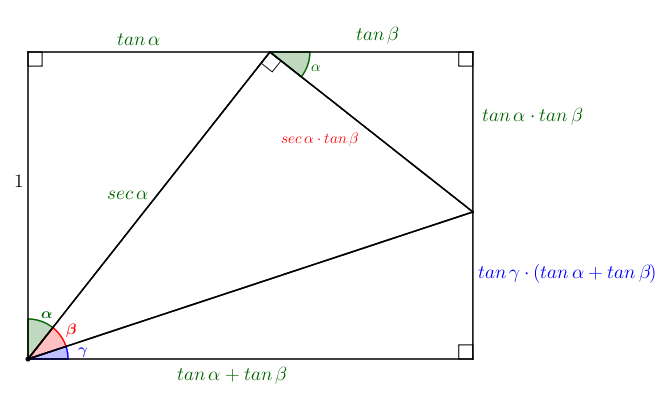
(Aqui, a explicação necessária para se obter o resultado é bem curtinha mesmo:devido às perpendicularidades mostradas na imagem, os lados opostos do quadrilátero externo têm a mesma medida. Particularmente, a igualdade entre os comprimentos dos lados verticais é a própria igualdade a ser mostrada. Relações trigonométrica justificam os comprimentos dos diversos triângulos da figura.)
A dedução
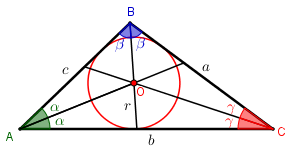
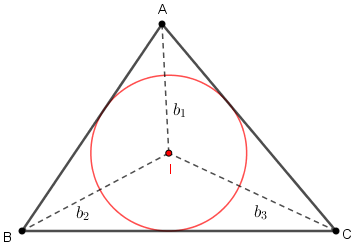
Seja [tex]ABC[/tex] um triângulo com lados medindo [tex]a, b[/tex] e [tex]c\, [/tex], conforme ilustramos na figura ao lado. Nessa figura também estão representadas as bissetrizes dos ângulos internos do triângulo [tex]ABC\, [/tex], assim como as medidas dos seis ângulos por elas determinados (dois a dois congruentes). Lembramos que as bissetrizes internas de um triângulo são concorrentes, e o ponto de encontro delas é o incentro, que é o centro da circunferência inscrita no triângulo, a qual também aparece na figura.
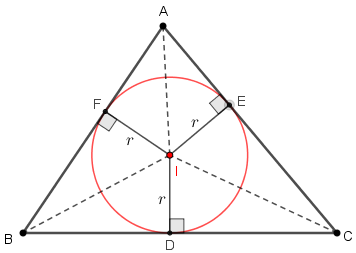
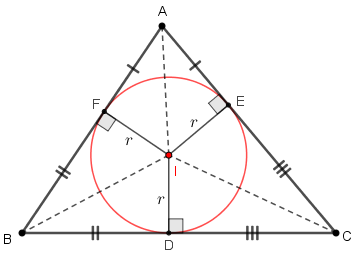
- Agora, observe com calma a figura abaixo. Nela aparecem o triângulo [tex]ABC\, [/tex], a sua circunferência inscrita e os raios, com medida [tex]r[/tex], nos pontos de tangência dessa circunferência com os lados do triângulo. (Lembramos que os segmentos definidos pelo centro da circunferência inscrita e pelos pontos de tangência formam ângulos retos com os respectivos lados intersectados do triângulo. Lembramos também que as distâncias de cada vértice do triângulo aos pontos de tangência dos lados definidos por esse vértice são iguais; essas distâncias estão representadas na figura por [tex]x,\, y\, [/tex] e [tex]\, z[/tex].) Finalmente, para simplificar a visualização, substituímos as três bissetrizes pelos respectivos segmentos [tex]\overline{OA}\, [/tex], [tex]\overline{OB}\, [/tex] e [tex]\overline{OC}\, [/tex] nelas contidos.
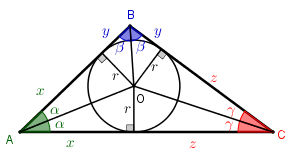
Pronto, já podemos fazer a dedução.
- Observe inicialmente, que o semiperímetro [tex]p[/tex] do triângulo [tex]ABC[/tex] satisfaz as seguintes igualdades:
[tex]\qquad p=\dfrac{a+b+c}{2}=x+y+z=x+a=y+b=z+c. \qquad \textcolor{#800000}{(i)}[/tex] - Por outro lado, como a soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex], então
[tex]2\alpha+2\beta+2\gamma=180^{\circ}[/tex].
Assim, [tex]\alpha+\beta+\gamma=90^{\circ}[/tex] e podemos, então, aplicar o Lema 2 às medidas [tex]\, \alpha\, ,\, \beta\, ,\, \gamma\, [/tex].
Portanto, segue que:
[tex]\qquad \tan\,\alpha\cdot \tan\,\beta+ \tan\,\gamma \cdot \tan\,\alpha +\tan \gamma \, \cdot \tan\,\beta= 1[/tex]
[tex]\qquad \dfrac{r}{x}\cdot \dfrac{r}{y}+ \dfrac{r}{z} \cdot \dfrac{r}{x} +\dfrac{r}{z} \cdot \dfrac{r}{y}= 1[/tex]
[tex]\qquad r^2 \cdot \left(\dfrac{1}{x \cdot y}+ \dfrac{1}{z \cdot x} +\dfrac{1}{z \cdot y}\right)= 1[/tex]
[tex]\qquad r^2 \cdot \dfrac{x+y+z}{x \cdot y \cdot z}= 1[/tex]
[tex]\qquad r^2 \cdot \dfrac{p}{x \cdot y \cdot z}\stackrel{\textcolor{#800000}{(i)}}{=} 1[/tex]
[tex]\qquad\dfrac{ \left(r \cdot p \right)^2}{x \cdot y \cdot z \cdot p}= 1 . \qquad \textcolor{#800000}{(ii)}[/tex]
Mas, pelo Lema 1, temos que [tex]A_t=r \cdot p[/tex]; logo, segue de [tex]\textcolor{#800000}{(ii)}[/tex] que:
[tex]\qquad\dfrac{ \left(A_t \right)^2}{x \cdot y \cdot z \cdot p}= 1[/tex]
[tex]\qquad\left(A_t \right)^2= \textcolor{#006400}{x} \cdot \textcolor{#0000CC}{y} \cdot \textcolor{#FF0000}{z} \cdot p \stackrel{\textcolor{#800000}{(i)}}{=} \textcolor{#006400}{(p-a)} \cdot \textcolor{#0000CC}{(p-b)} \cdot \textcolor{#FF0000}{(p-c)} \cdot p.[/tex]
Como [tex]A_t \gt 0[/tex], pois é uma área, concluímos que [tex]\, \fcolorbox{black}{#eee5de}{$A_t=\sqrt{p \cdot (p-a) \cdot (p-b)\cdot (p-c)}$}\, [/tex], que é a fórmula de Herão.
Equipe COM – OBMEP