Problema
(Indicado a partir do 9º ano do E. F.)
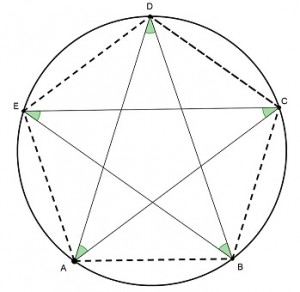
A Estrela de Cinco Pontas, também denominada Estrela Pentagonal ou Pentagrama, é de origem Pitagórica e pode ser construída com seus vértices sobre um pentágono regular, como indica a figura abaixo. Sendo assim, determine a soma dos ângulos em destaque.
Solução 1
Pela propriedade da soma dos ângulos internos, se S for a soma dos ângulos internos do pentágono, então cada ângulo interno de um pentágono regular mede
m = S / n = [(n−2)180°] / n = [(5−2)180°] / 5 = 108°.
Em cada ponta, cada ângulo ai , i = 1, 2, … , 10, é suplementar com relação a um dos ângulos internos do pentágono regular interno à estrela, logo todos esses ângulos são congruentes e medem, respectivamente, mi = 180° −108° = 72°, para i = 1, 2, … , 10.
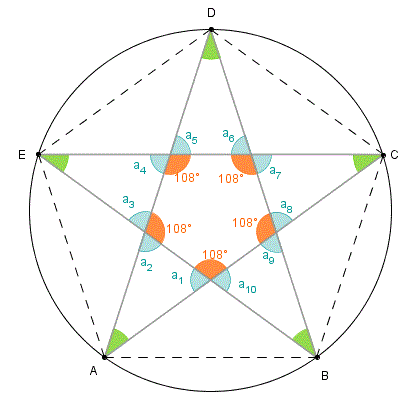
Com isso, os ângulos agudos formados pelas pontas medirão 180° −2 × 72° = 36°.
Agora, só multiplicamos essa medida pela quantidade de ângulos agudos de 36° formados, que seria 5 × 36° = 180° .
Solução elaborada pelo COM Fermatianos, com contribuições dos Moderadores do Blog.
Solução 2
Por conveniência, identificaremos os ângulos indicados em verde por [tex]\hat{A}[/tex], [tex]\hat{B}[/tex], [tex]\hat{C}[/tex], [tex]\hat{D}[/tex] e [tex]\hat{E}\,.[/tex]
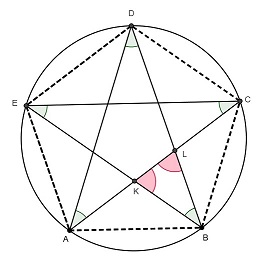
Observe, na figura abaixo, que os ângulos [tex]B\hat{K}L[/tex] e [tex]K\hat{L}B[/tex] são externos aos triângulos [tex]\triangle EKC[/tex] e [tex]\triangle ALD[/tex], respectivamente. Sendo assim, temos que [tex]B\hat{K}L=\hat{E}+\hat{C}[/tex] e [tex]K\hat{L}B=\hat{D}+\hat{A}[/tex], pelo Teorema do Ângulo Externo (*).
Logo,
[tex]\quad \hat{A}+\hat{B}+\hat{C}+\hat{D}+\hat{E}=(\hat{E}+\hat{C})+(\hat{A}+\hat{D})+\hat{B}=B\hat{K}L+K\hat{L}B+\hat{B}=180^{\circ},[/tex]
já que [tex]B\hat{K}L\,[/tex] , [tex]\,K\hat{L}B\,[/tex] e [tex]\,\hat{B}\,[/tex] são ângulos internos do triângulo [tex]\triangle KLB[/tex].
(*) Você pode encontrar o teorema do ângulo externo AQUI.
Solução elaborada pelos Moderadores do Blog.
Solução 3
Duas observações iniciais:
- Se [tex]a_i[/tex] for a medida, em graus, de cada ângulo interno de um pentágono regular e se [tex]S_i[/tex] for a soma dos ângulos internos do pentágono, então [tex]a_i=108^{\circ}[/tex], uma vez que [tex]a_i = \dfrac{S_i}{n}=\dfrac{(5-2)180^{\circ}}{5} =\dfrac{540^{\circ}}{5} = 108^{\circ}[/tex].
- Os triângulos [tex]ABE\, ,\, BCA \, ,\, CDB \, , \, DEC \, , \, EAD\, [/tex] têm dois lados congruentes (lados do pentágono regular inicial), então eles são isósceles e seus dois ângulos de base respectivos medem [tex]\dfrac{180^{\circ}-108^{\circ}}{2}=36^{\circ}[/tex].
Para cada ponta fixada da estrela, seja ae a medida em graus de cada um dos chamados ângulos externos do pentágono interno à estrela (todos têm a mesma medida). Observe que trata-se de um ângulo externo a um triângulo isósceles com ângulos da base medindo 36°, assim, pelo Teorema do Ângulo Externo (*), [tex]a_e = 36^{\circ} + 36^{\circ}[/tex], ou seja, [tex]a_e = 72^{\circ}[/tex].
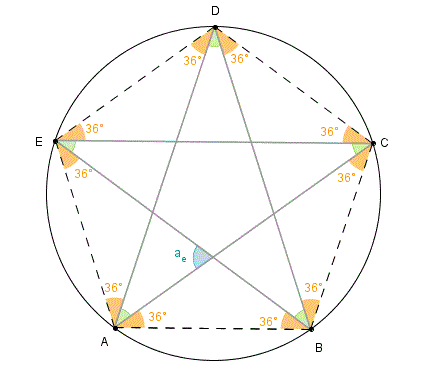
Como [tex]a_e=72^{\circ}[/tex], então cada ângulo formado pelas pontas da estrela medirá [tex] 180^{\circ}-2 \times 72^{\circ} = 36^{\circ}[/tex].
Assim, a soma a ser determinada é dada por [tex]5 \times 36^{\circ}= 180^{\circ} [/tex]; ou seja, a soma das medidas dos ângulos em destaque verde será igual a [tex]180^{\circ}[/tex].
(*) Você pode encontrar o teorema do ângulo externo AQUI.
Solução elaborada pelos Moderadores do Blog.
Solução 4
Unindo as pontas do Pentagrama, obtemos um pentágono regular onde cada ângulo interno [tex](a_i)[/tex] mede [tex]108^o[/tex].
[tex]\qquad a_i = \dfrac{S_i}{n}=\dfrac{(5-2)180^{\circ}}{5} =\dfrac{540^{\circ}}{5} = 108^{\circ}[/tex]
sendo [tex]S_i[/tex] a soma dos ângulos internos do pentágono.
O mesmo acontece com o pentágono regular no interior do pentagrama.
O Pentagrama é formado pelo pentágono regular e cinco triângulos isósceles cujas bases são os lados do pentágono interno. Desse modo, os ângulos relativos à base desses triângulos correspondem ao ângulo externo do pentágono interno, ou seja, os ângulos das bases desses triângulos medem [tex]72^o[/tex].
Indicando a medida de cada um dos ângulos em verde por [tex]x[/tex] temos que [tex]72^{\circ}+ 72^{\circ} + x = 180^{\circ}[/tex] e, assim, [tex]x=36^{\circ}[/tex].
Portanto, a soma dos ângulos em verde é [tex]5 \times 36^{\circ} = 180^{\circ}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 5
Nesta solução, denotaremos os ângulos indicados em verde por [tex]\hat{A}[/tex], [tex]\hat{B}[/tex], [tex]\hat{C}[/tex], [tex]\hat{D}[/tex] e [tex]\hat{E}[/tex] e suas respectivas medidas, em graus, por [tex]a , b, c, d, e [/tex].
Observamos, inicialmente, que se [tex]a_i[/tex] for a medida, em graus, de cada ângulo interno de um pentágono regular e se [tex]S_i[/tex] for a soma dos ângulos internos do pentágono, então [tex]a_i=108^{\circ}[/tex], uma vez que
[tex]\quad a_i = \dfrac{S_i}{n}=\dfrac{(5-2)180^{\circ}}{5} =\dfrac{540^{\circ}}{5} = 108^{\circ}[/tex].
Por outro lado, os triângulos [tex]ABE\, ,\, BCA \, ,\, CDB \, , \, DEC \, , \, EAD [/tex] têm dois lados congruentes (lados do pentágono regular inicial), então eles são isósceles e seus dois ângulos de base respectivos medem [tex]\dfrac{180^{\circ}-108^{\circ}}{2}=36^{\circ}[/tex].
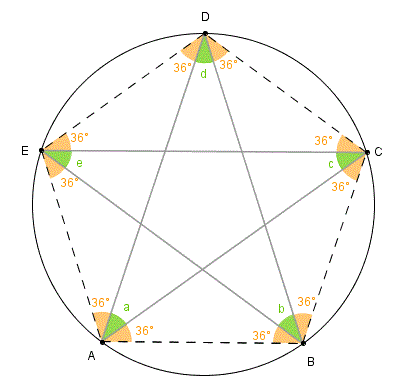
Assim, os ângulos [tex]\hat{A}[/tex], [tex]\hat{B}[/tex], [tex]\hat{C}[/tex], [tex]\hat{D}[/tex] e [tex]\hat{E}[/tex] têm a mesma medida e
[tex] a = b = c = d = e =108^{\circ}-36^{\circ}-36^{\circ}=108^{\circ}-72^{\circ}=36^{\circ}[/tex].
Portanto, a soma das medidas dos ângulos agudos em destaque será igual a
[tex] a + b + c + d + e =5 \times 36^{\circ}=180^{\circ}.[/tex]
Solução elaborada pelos Moderadores do Blog.
