✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 2º ano do E. M.)
Um laboratório testa a periculosidade de fungos desconhecidos. Estima-se que o teste forneça falsos negativos em 2% dos fungos tóxicos, enquanto rotula como perigosos 5% dos fungos inofensivos.
O professor Thiago observa com cautela que, mesmo que o teste classifique certo tipo de fungo como tóxico, ele tem 50% de chance de não o ser. Tomando como verdade a afirmação do professor Thiago, sua assistente Abigail inferiu que x% dos tipos de fungos analisados são tóxicos.
Calcule x.

Lembretes e notações
✏ Probabilidade condicional: Dados dois eventos [tex]A[/tex] e [tex]B[/tex], a probabilidade condicional de [tex]A[/tex] ocorrer dado que [tex]B[/tex] ocorre é denotada por [tex]P(A|B)[/tex] e calculada da seguinte forma:
[tex]\quad \boxed{P(A\mid B)=\dfrac{P(A\cap B)}{P(B)}=\dfrac{\text{probabilidade de A ocorrer e B ocorrer}}{\text{probabilidade de B ocorrer}}}.[/tex]
Para aprender um pouco mais sobre esse assunto, visite esta Sala do nosso Blog: Probabilidade Condicional (Um primeiro estudo).
✏ Princípio Fundamental da Contagem para dois eventos: Se
- um evento E1 puder ocorrer de [tex] m_1 [/tex] maneiras,
- e um evento E2 puder ocorrer de [tex]m_2 [/tex] maneiras,
e esses dois eventos forem independentes entre si (isto é, a ocorrência de um não muda a quantidade de possibilidades para a ocorrência do outro), então a quantidade de maneiras em que os dois eventos ocorrem ao mesmo tempo é
[tex]\qquad \qquad \boxed{m_1\times m_2} \,.[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
Este é um problema que envolve probabilidade condicional, já que precisaremos calcular a probabilidade de um fungo ser tóxico, sabendo que o teste deu positivo.
Vamos, então estudar a probabilidade [tex]P(\text{fungo tóxico}\mid\text{ teste positivo}).[/tex]
Pela informação do professor Thiago, sabemos que esta probabilidade é de apenas [tex]50\%[/tex]. Observe, pela fórmula dada acima, que:
[tex]\qquad P(\text{fungo tóxico}\mid\text{ teste positivo})=\dfrac{\text{probabilidade de o fungo ser tóxico e o teste dar positivo}}{\text{probabilidade do teste dar positivo}}[/tex].
- Se [tex]x\%[/tex] dos fungos são tóxicos, a probabilidade do fungo ser tóxico é [tex]x\%[/tex]. Quando ele é tóxico, o teste oferece um falso negativo com [tex]2\%[/tex] de chance; assim, oferece resultado correto em [tex]98\%[/tex] dos casos.
Isso implica que, pelo Princípio Fundamental da Contagem, a probabilidade do fungo ser tóxico e o teste dar positivo é dada por:
[tex]\qquad x\%\times 98\%=\dfrac{x}{100}\times \dfrac{98}{100}=\dfrac{98x}{10000}[/tex]. - Por outro lado, o teste dá positivo em dois casos: quando o fungo não é tóxico ([tex]5\%[/tex] de chance de dar um falso positivo) e quando o fungo realmente é tóxico ([tex]98\%[/tex] de chance de dar um positivo correto).
Como [tex](100-x)\%[/tex] dos fungos não são tóxicos, pelo Princípio Fundamental da Contagem, há uma probabilidade de
[tex]\qquad (100-x)\%\times5\%=\dfrac{100-x}{100}\times\dfrac{5}{100}=\dfrac{500-95x}{10000} [/tex]
do primeiro caso ocorrer.
A probabilidade do segundo caso já foi calculada: [tex]x\%\times 98\%=\dfrac{x}{100}\times \dfrac{98}{100}=\dfrac{98x}{10000}[/tex].
Assim,
[tex]\qquad P(\text{fungo tóxico}\mid\text{ teste positivo})=\dfrac{\dfrac{98x}{10000}}{\dfrac{500-5x}{10000} +\dfrac{98x}{10000}}[/tex]
[tex]\qquad P(\text{fungo tóxico}\mid\text{ teste positivo})=\dfrac{98x}{500-5x+98x}=50\%\,.[/tex]
Daí, segue que:
[tex]\qquad \dfrac{98x}{500+93x}=\dfrac{50}{100}\\
~~[/tex]
[tex]\qquad9800x=25000+4650x[/tex]
[tex]\qquad5150x=25000[/tex]
[tex]\qquad x\approx 4,85.[/tex]
Portanto, aproximadamente [tex]4,85\%[/tex] dos fungos são tóxicos.
 Confuso?
Confuso? Este tipo de raciocínio é um pouco incomum e quase contraintuitivo. Para facilitar a compreensão, podemos fazer uma tabela e estipular um valor numérico para a população testada. Isso facilita o raciocínio.
Por exemplo, suponha que temos uma população de [tex]10\,000[/tex] fungos. Assim,
- [tex]x\%[/tex] dos fungos são realmente tóxicos, isto é, [tex]100x[/tex];
- [tex](100-x)\%[/tex] dos fungos não são tóxicos, isto é, [tex]10 000 -100x[/tex];
- Dos [tex]100x[/tex] fungos tóxicos, [tex]98\%[/tex] são classificados como tal, ou seja, [tex]98x[/tex];
- Dos [tex]10 000 -100x[/tex] fungos inofensivos, [tex]5\%[/tex] são classificados como tóxicos, ou seja, [tex]500 – 5x[/tex].
Podemos montar a seguinte tabela:
| Teste positivo | Teste Negativo | |
| Fungos tóxicos | [tex]\,98x[/tex] | [tex]~100x-98x=2x[/tex] |
| Fungos inofensivos | [tex]500-5x[/tex] | [tex]10\,000-100x-\left(500-5x \right)=9\,500-95x[/tex] |
A probabilidade de um fungo ser tóxico dado que seu exame foi positivo é, então, [tex]\dfrac{98x}{98x+500-5x}=50\%[/tex].
Assim, segue que:
[tex]\qquad \dfrac{98x}{93x+500}=\dfrac{50}{100}[/tex]
[tex]\qquad 9800x=4650x+25000[/tex],
donde concluímos que [tex]x\approx 4,85[/tex].
Outro recurso didático que facilita a visualização é o diagrama de árvore:
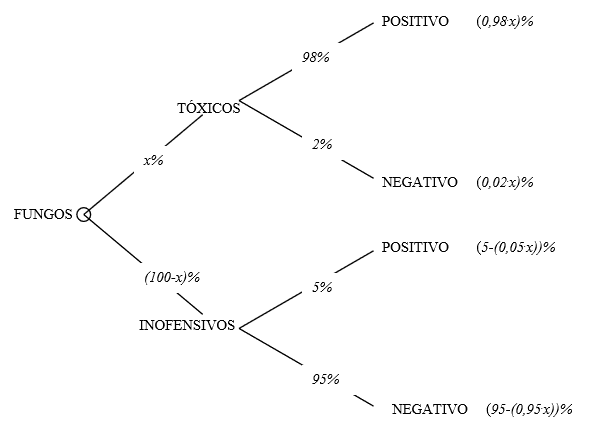
A probabilidade de um fungo ser tóxico dado que seu exame foi positivo é, então,
[tex]\qquad \dfrac{(0,98\cdot x)\%}{(0,98\cdot x)\%+(5-(0,05\cdot x))\%}=50\%[/tex].
Assim, [tex]x\approx 4,85[/tex].
Solução elaborada pelos Moderadores do Blog.
