Problema
(Indicado a partir do 2º ano do E. M.)
(FUVEST, 2009 – Adaptado) Seis times de futebol, entre os quais estão [tex]A[/tex] e [tex]B[/tex], vão disputar um campeonato. Suponha que na classificação final não existam empates. Um indivíduo fez duas apostas sobre a classificação final. Na primeira, apostou que [tex]A[/tex] não seria campeão; na segunda, apostou que [tex]B[/tex] seria o último colocado.
Responda:
a) Quantas são as classificações possíveis?
b) Em quantas classificações possíveis esse indivíduo ganha?

Lembrete
✏ Dados conjuntos, [tex]C_1[/tex] e [tex]C_2[/tex], o número de elementos da união desses dois conjuntos é dado por:
[tex]\qquad \qquad \boxed{n(C_1 \cup C_2)=n(C_1)+n(C_2)-n(C_1 \cap C_2)}[/tex].
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas,
- e todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então o número total de maneiras de tomarmos sucessivamente essas [tex]k[/tex] decisões é igual ao produto
[tex]\qquad \qquad \boxed{m_1\cdot m_2 \cdot \ldots \cdot m_k}\, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
a) Pelo Princípio Fundamental da Contagem, temos um total de [tex]6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1=720[/tex] classificações possíveis.
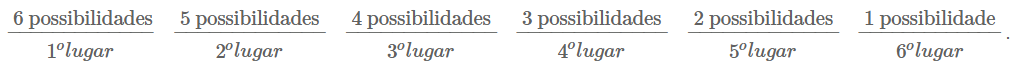
b) Já sabemos que o total de classificações possíveis é [tex]720[/tex]. Agora, calculemos:
- O número de classificações em que [tex]A[/tex] não é primeiro lugar.
- O número de classificações em que [tex]B[/tex] é o último lugar.
Temos [tex]5[/tex] possibilidade para a primeira posição, [tex]5[/tex] para a segunda, [tex]4[/tex] para a terceira, [tex]3[/tex] para a quarta, [tex]2[/tex] para a quinta e [tex]1[/tex] para a sexta. Logo, temos um total de [tex]5\cdot 5\cdot 4\cdot 3\cdot 2 \cdot 1=600[/tex].
Temos [tex]5[/tex] possibilidades para a primeira posição, [tex]4[/tex] para a segunda, [tex]3[/tex] para a terceira, [tex]2[/tex] para a quarta, [tex]1[/tex] para a quinta e [tex]1[/tex] para a sexta. Assim, temos um total de [tex]5 \cdot 4\cdot 3\cdot 2\cdot 1 \cdot 1=120[/tex].
Agora, vejamos quantos casos correspondem à intersecção dos dois casos anteriores, ou seja, [tex]A[/tex] não é primeiro e [tex]B[/tex] é o último. Temos [tex]4[/tex] possibilidades para a primeira posição, [tex]4[/tex] para a segunda, [tex]3[/tex] para a terceira, [tex]2[/tex] para a quarta, [tex]1[/tex] para a quinta e [tex]1[/tex] para a sexta. Portanto, temos um total de [tex]4 \cdot 4\cdot 3\cdot 2\cdot 1 \cdot 1=96[/tex].
Desta forma, são [tex]600+120-96=624[/tex] classificações possíveis para ele ganhar a aposta.
Utilizando os nosso cálculos, poderíamos ilustrar a resposta do problema por meio de um diagrama de Venn:
- Seja [tex]X[/tex] o conjunto do número de classificações em que [tex]A[/tex] não é primeiro lugar e [tex]Y[/tex] o conjunto do número de classificações em que [tex]B[/tex] é o último lugar. Como a intersecção dos conjuntos citados é [tex]96[/tex], temos o diagrama abaixo.
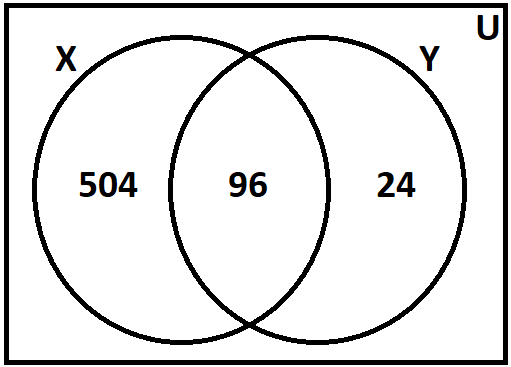
Portanto, a quantidade de casos pedidos é [tex]504+96+24=624[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
