✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de Dificuldade: Muito difícil)
(OPM – 2005) Foram traçadas três retas paralelas passando pelos vértices [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex] do quadrado [tex]ABCD[/tex], conforme mostra a figura.
A reta que passa por [tex]C[/tex] dista [tex]7 \, cm[/tex] da que passa por [tex]B[/tex] e [tex]5 \, cm[/tex] da que passa por [tex]D[/tex].
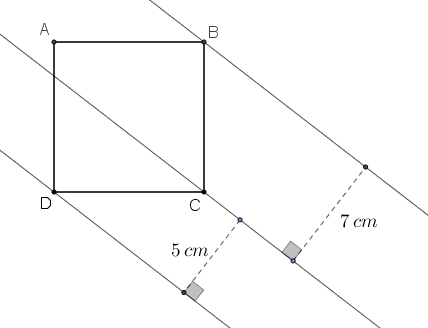
Qual a área do quadrado [tex]ABCD[/tex]?

Lembretes
(1) A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex].
(2) Ângulos alternos internos têm a mesma medida. (Se você não se lembra dos ângulos alternos internos, clique AQUI.)
(3) Caso de congruência L.A.Ao. (lado – ângulo – ângulo oposto): Se dois triângulos têm ordenadamente congruentes um lado, um ângulo adjacente e o ângulo oposto a esse lado, então estes triângulos são congruentes. (Se você não se lembra dos casos de congruência de triângulos, clique AQUI.)
Solução
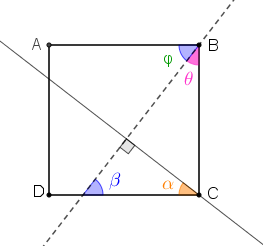 Das três paralelas que aparecem na imagem do enunciado do problema, vamos, inicialmente, observar apenas a que passa por [tex]C \, [/tex] e traçar uma perpendicular a ela que passa pelo ponto [tex]B \, .[/tex]
Das três paralelas que aparecem na imagem do enunciado do problema, vamos, inicialmente, observar apenas a que passa por [tex]C \, [/tex] e traçar uma perpendicular a ela que passa pelo ponto [tex]B \, .[/tex]Vamos observar com cuidado os quatro ângulos cujas medidas [tex]\alpha \, [/tex], [tex]\beta \, [/tex], [tex]φ \, [/tex] e [tex] \, \theta \, [/tex] aparecem destacadas na figura ao lado e para isso consideraremos as medidas dos ângulos em graus.
- Perceba que os ângulos cujas medidas são [tex]\beta \, [/tex] e [tex] \, φ \, [/tex] são alternos internos, logo [tex]\boxed{\beta=φ} \, .\quad \textcolor{#800000}{(i)}[/tex]
- Note que os ângulos cujas medidas são [tex]\theta \, [/tex] e [tex] \, φ \, [/tex] são ângulos complementares, isto é, [tex]\theta+φ=90^\circ \, [/tex]. Mas, por [tex]\textcolor{#800000}{(i)} \, [/tex], [tex]\beta=φ \, [/tex], portanto [tex]\theta+\beta=90^\circ \, [/tex] e, então, [tex]\boxed{\beta=90^\circ-\theta} \, .\quad \textcolor{#800000}{(ii)}[/tex]
- Como a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ \, [/tex], podemos concluir que [tex]\alpha+\beta+90^\circ=180^\circ \, [/tex] e, assim, [tex]\alpha+\beta=90^\circ \, .[/tex] No entanto, por [tex]\textcolor{#800000}{(ii)} \, [/tex], [tex]\boxed{\beta=90^\circ-\theta} \, [/tex]; logo, segue que:
[tex]\alpha+\beta=90^\circ \, [/tex]
[tex]\alpha+\left(\cancel{90^\circ}-\theta\right)=\cancel{90^\circ} \, [/tex]
[tex]\boxed{\alpha=\theta} \, .\quad \textcolor{#800000}{(iii)}[/tex]
Considere agora os segmentos [tex]\overline{DE}[/tex] e [tex]\overline{BF}[/tex], perpendiculares às retas paralelas.
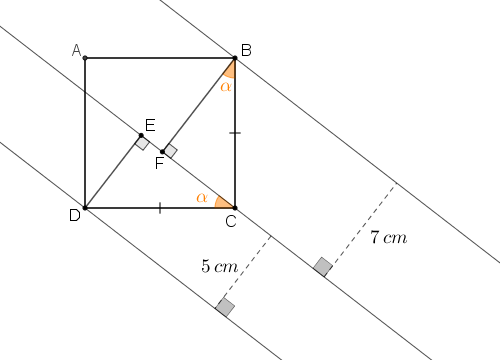
Veja que, utilizando o Caso de congruência L.A.Ao., podemos concluir que os triângulos [tex]BCF \, [/tex] e [tex] \, CDE[/tex] são congruentes e, consequentemente, os segmentos [tex]\overline{DE} \, [/tex] e [tex] \, \overline{CF}[/tex] têm o mesmo tamanho: [tex]5 \, cm[/tex] (Assim como [tex]\overline{FB} \, [/tex] e [tex] \, \overline{EC}[/tex]: [tex]7 \, cm[/tex].).
Dessa forma, podemos aplicar o Teorema de Pitágoras em qualquer um dos triângulos [tex]BCF \, [/tex] e [tex] \, CDE[/tex]. Portanto, se [tex]l[/tex] é o lado do quadrado [tex]ABCD \, [/tex], segue que:
[tex]\qquad l^2=5^2+7^2=25+49=74 \, cm^2 \, .[/tex]
Como [tex]l^2[/tex] é exatamente a área do quadrado [tex]ABCD \, [/tex], finalmente podemos concluir que a área do quadrado [tex]ABCD \, [/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$74 \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
