✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 1º ano do E. M. – Nível de dificuldade: Médio)
(XVI Concurso Primavera de Matemáticas, 2012) Duas circunferências de perímetro [tex]9~\text{cm}[/tex] cada foram desenhadas em uma folha de papel, de modo que cada uma passasse pelo centro da outra, resultando a figura abaixo.
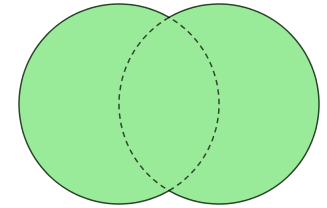
Qual o perímetro da figura colorida?

Ajudas
(1) A um arco de circunferência podemos associar duas medidas distintas:
✐ a sua medida angular (em graus ou radianos), [tex]\alpha[/tex];
✐ a sua medida linear (em unidades de comprimento), [tex]c[/tex].
Conhecida uma delas, a outra pode ser obtida a partir da medida angular e do comprimento da circunferência que define o arco por meio de uma regra de três simples:
| [tex]2\pi \, r[/tex] | ————————————– | [tex]360^\circ[/tex] |
| [tex]c[/tex] | ————————————– | [tex]\alpha[/tex] |
Se você não se lembra disso, não faz mal: clique AQUI.
(2) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução
O perímetro da figura colorida em verde é o perímetro dos arcos destacados em verde na figura abaixo. Veja que esse perímetro pode ser obtido fazendo-se a diferença entre o perímetro das duas circunferências (arcos azuis) e o comprimento da linha destacada em vermelho: [tex]\textcolor{#00CC00}{P_{verde}}=\textcolor{#0099FF}{P_{azul}}-\textcolor{#FF0000}{P_{verm}}\,.[/tex]
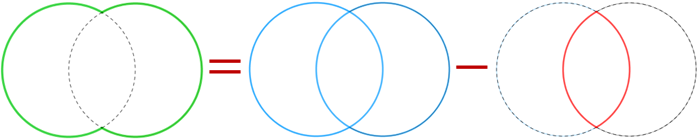
Como conhecemos o perímetro de cada circunferência, e portanto o [tex]\textcolor{#0099FF}{P_{azul}}[/tex], só precisaremos calcular o perímetro vermelho.
Para isso, observe que os dois triângulos mostrados na figura abaixo são definidos por raios das duas circunferências; logo, são triângulos isósceles e seus ângulos internos medem [tex]60^{\circ}\,.[/tex]
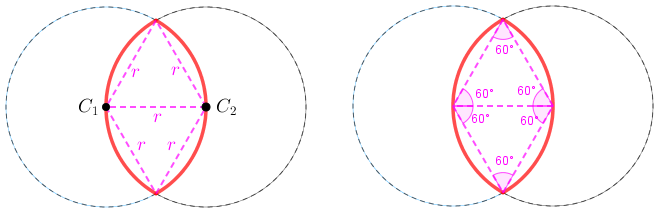
Dessa forma, o perímetro vermelho, [tex]\textcolor{#FF0000}{P_{verm}}\,[/tex], corresponde ao perímetro de quatro arcos de [tex]60^{\circ}\,[/tex] definidos nas duas circunferências, ou de dois arcos de [tex]120^{\circ}\,.[/tex]
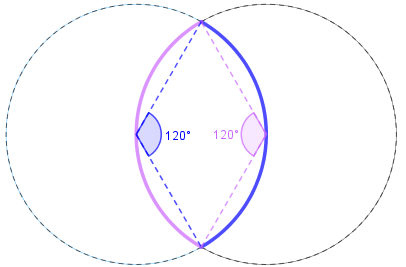
A Ajuda (2) nos indica que podemos determinar o comprimento [tex]c[/tex] de um arco [tex]120^{\circ}\,[/tex] definido em qualquer uma das circunferências de perímetro [tex]9\, \text{cm}[/tex] utilizando uma regrinha de três simples.
| [tex]9\, \text{cm}[/tex] | ————————————– | [tex]360^\circ[/tex] |
| [tex]c[/tex] | ————————————– | [tex]120^{\circ}[/tex] |
Então
[tex]\qquad \qquad c=\dfrac{120^{\circ} \cdot 9}{360^{\circ}}=3\, \text{cm}[/tex]
e, portanto,
[tex]\qquad \qquad \textcolor{#FF0000}{P_{verm}=6\,\text{cm}}\,.[/tex]
Como [tex]\textcolor{#00CC00}{P_{verde}}=\textcolor{#0099FF}{P_{azul}}-\textcolor{#FF0000}{P_{verm}}\,[/tex], segue que:
[tex]\qquad \qquad \textcolor{#00CC00}{P_{verde}}=\textcolor{#0099FF}{2 \cdot 9}-\textcolor{#FF0000}{6}\\
\qquad \qquad \textcolor{#00CC00}{P_{verde}=12\, \text{cm}\,}.[/tex]
Assim, o perímetro da figura colorida fornecida no problema é [tex]\fcolorbox{black}{#dfd}{$12\, \text{cm}$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
