.Problema para ajudar na escola: Cinco letras

Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)

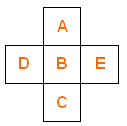
Vamos substituir as letras [tex]A\, ,\, B\, ,\, C\, ,\, D\, ,\, E[/tex] da figura abaixo pelos números [tex]1[/tex], [tex]2[/tex], [tex]3[/tex], [tex]4[/tex], [tex]5[/tex], sem repetição, de modo que [tex]\, A+B+C\, [/tex] e [tex]\, D+B+E\, [/tex] sejam múltiplos de [tex]3\, [/tex].
De quantas maneiras podemos fazer isso?

Solução

Sabemos que [tex]\, A+B+C\, [/tex] e [tex]\, D+B+E\, [/tex] são múltiplos de [tex]3\, [/tex]; assim:
► a soma [tex](A+B+C)+(D+B+E)[/tex] é também um múltiplo de [tex]3.[/tex]
Mas
[tex]\qquad \begin{align*}(A+B+C)+(D+B+E)&=\underbrace{(A+B+C+D+E)}_{1+2+3+4+5}+B\\
&=15+B \end{align*}[/tex]
logo, [tex]\boxed{B=(A+B+C)+(D+B+E)-15}.[/tex]
Como [tex]\boxed{(A+B+C)+(D+B+E)}\, [/tex] e [tex]\, \boxed{15}[/tex] são múltiplos de [tex]3[/tex], então
► [tex]B[/tex] é também um múltiplo de [tex]3[/tex]
e, dessa forma, a única possibilidade para [tex]B\, [/tex] é [tex]\, \boxed{B=3}\, [/tex], já que [tex]B \in \{1,2,3,4,5\}.[/tex]
Mas cada soma [tex]\, A+B+C\, [/tex] e [tex]\, D+B+E\, [/tex] é um múltiplo de [tex]3[/tex] e [tex]B=3[/tex]; portanto, podemos concluir que
► [tex]A+C\, [/tex] é um múltiplo de [tex]3[/tex]
► [tex]D+E\, [/tex] é um múltiplo de [tex]3[/tex]
uma vez que diferença de múltiplos de [tex]3[/tex] é um múltiplo de [tex]3.[/tex]
Sendo [tex]A+C\, [/tex] um múltiplo de [tex]3[/tex], temos então oito escolhas para os números [tex]A\, [/tex] e [tex]\, C[/tex]:

• [tex]A=1[/tex] e [tex]\, C=2\, [/tex],
• [tex]A=1[/tex] e [tex]\, C=5\, [/tex],
• [tex]A=2[/tex] e [tex]\, C=1\, [/tex],
• [tex]A=2[/tex] e [tex]\, C=4\, [/tex],
• [tex]A=4[/tex] e [tex]\, C=2\, [/tex],
• [tex]A=4[/tex] e [tex]\, C=5\, [/tex],
• [tex]A=5[/tex] e [tex]\, C=1\, [/tex],
• [tex]A=5[/tex] e [tex]\, C=4\, [/tex].

Conhecidos os valores de [tex]A\, [/tex] e [tex]\, C[/tex], automaticamente saberemos quais são os dois valores possíveis para [tex]D\, [/tex] e [tex]\, E[/tex]; no entanto, perceba que podemos associar esses dois valores de duas maneiras distintas: para [tex]D\, [/tex] e [tex]\, E[/tex], nessa ordem, ou para [tex]E\, [/tex] e [tex]\, D[/tex], nessa ordem.

[tex]\begin{array}{c c c c c}
1&\, \, \, &8&\, \, \, &2\\
\overline{ \text{escolha para B}\, }&\, \, \, &\, \overline{ \text{escolhas para A e C}\, }&\, \, \, &\, \overline{ \text{escolhas para D e E}\, }
\end{array}[/tex]

Assim, o número de modos distintos de substituirmos as letras pelos números, de acordo com as regras apresentadas, é [tex]\, \fcolorbox{black}{#eee0e5}{$1 \times 8 \times 2=16$}\, .[/tex]

Solução elaborada pelos Moderadores do Blog.