✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
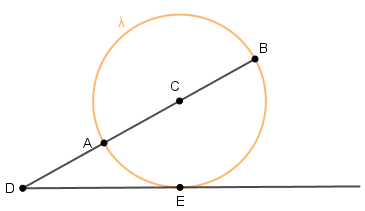
Na figura, [tex]A[/tex], [tex]B[/tex] e [tex]E[/tex] são pontos da circunferência [tex]\lambda[/tex] cujo centro é [tex]C[/tex].
Se [tex]\overline{AB}[/tex] é um diâmetro, [tex]E[/tex] é um ponto de tangência e as medidas dos arcos [tex]\stackrel{\frown}{AE}[/tex] e [tex]\stackrel{\frown}{EB}[/tex] são [tex]10 \, [/tex]cm e [tex]20 \, [/tex]cm, respectivamente, qual é a medida em graus do ângulo [tex]B\hat{D}E[/tex]?
E em radianos?

Ajudas
✐ A um arco de circunferência podemos associar duas medidas distintas:
– a sua medida angular;
– a sua medida linear.
Ambas podem ser obtidas a partir da medida angular e do comprimento da circunferência que define o arco; mas, se você não se lembra delas, clique AQUI. (Não se esqueça de fechar a janelinha que se abriu com as informações, depois de utilizá-la.)
✐ Toda tangente a uma circunferência é perpendicular ao raio no ponto de tangência.
✐ A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex].
Solução
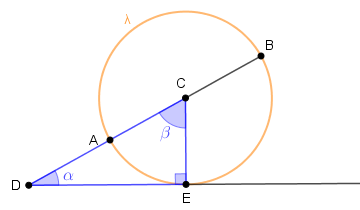
Utilizando a segunda ajuda, observamos que [tex]B\hat{D}E[/tex] é um dos ângulos agudos internos do triângulo retângulo [tex]CED \, [/tex], assinalado na figura abaixo. Assim, para obtermos a medida [tex]\alpha[/tex] do ângulo [tex]B\hat{D}E[/tex] em questão, basta conhecermos a medida [tex]\beta[/tex] do ângulo central [tex]D\hat{C}E \, [/tex], já que, conforme a terceira ajuda, a soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ} \, .[/tex]
 Vamos lá!
Vamos lá!
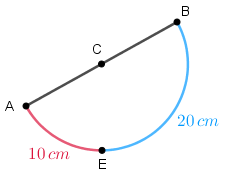
Pelos dados do problema, as medidas dos arcos [tex]\stackrel{\frown}{AE}[/tex] e [tex]\stackrel{\frown}{EB}[/tex] são [tex]10 \, [/tex]cm e [tex]20 \, [/tex]cm; portanto, a medida do arco [tex]\stackrel{\frown}{AB}[/tex] é [tex]30 \, [/tex]cm.
Como [tex]\overline{AB}[/tex] é um diâmetro, o comprimento do arco [tex]\stackrel{\frown}{AB}[/tex] é o semiperímetro da circunferência [tex]\lambda[/tex] e, consequentemente, o comprimento de [tex]\lambda[/tex] é [tex]60 \,[/tex] cm.
Utilizando, agora, a primeira ajuda, observamos que uma regra de três simples resolve o problema de se determinar a medida [tex]\beta[/tex] do ângulo central. Vamos obter inicialmente as medidas em graus; depois faremos a conversão para radianos.
Armando a regra de três
[tex] \begin{array}{c c c}
60 \text{ cm} &\text{————–}&360^\circ\\
10 \text{ cm} &\text{————–}&\beta
\end{array}[/tex]
obtemos que:
[tex]\quad 60\times \beta=10\times360^\circ[/tex]
[tex]\quad \beta=\dfrac{3600^\circ}{60}[/tex]
[tex]\quad \boxed{\beta=60^\circ} \, .[/tex]
Observamos que poderíamos armar a regra de três a partir da informação de que o semiperímetro da circunferência [tex]\lambda[/tex] é [tex]30 [/tex]\, cm. Nesse caso, só teríamos que lembrar que o semiperímetro está associado ao ângulo raso de [tex]180^\circ[/tex] e, portanto, armaríamos a regra de três assim:
[tex] \begin{array}{c c c}
30 \text{ cm} &\text{————–}&180^\circ\\
10 \text{ cm} &\text{————–}&\beta
\end{array}[/tex]
e obteríamos que:
[tex]\quad 30\times \beta=10\times 180^\circ[/tex]
[tex]\quad \beta=\dfrac{1800^\circ}{30}[/tex]
[tex]\quad \boxed{\beta=60^\circ} \, .[/tex]
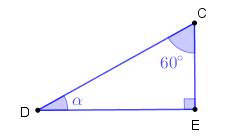
Com a medida [tex]\beta \, [/tex], podemos aplicar a terceira ajuda ao triângulo [tex]CDE[/tex] e obtermos:
[tex]\quad 60^\circ+\alpha+90^\circ=180^\circ[/tex]
[tex]\quad \alpha=180^\circ- 60^\circ-90^\circ[/tex]
[tex]\quad \boxed{\alpha=30^\circ} \, .[/tex]
Para obtermos a medida em radianos do ângulo [tex]B\hat{D}E[/tex], lembramos que, por exemplo, [tex]180^\circ[/tex] correspondem a [tex]\pi[/tex] radianos e fazemos mais uma regra de três simples:
[tex] \begin{array}{c c c}
180^\circ &\text{————–}&\pi \, radianos\\
30^\circ &\text{————–}&\alpha
\end{array}[/tex]
para obtermos:
[tex]\quad 30\pi=180\alpha[/tex]
[tex]\quad \alpha=\dfrac{30\pi}{180}[/tex]
[tex]\quad \boxed{\alpha=\dfrac{\pi}{6} \, radianos} \, .[/tex]
Então, a medida do ângulo [tex]B\hat{D}E[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$\alpha =30^\circ$} \, [/tex] ou [tex] \, \fcolorbox{black}{#eee0e5}{$\alpha =\dfrac{\pi}{6} \, radianos$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
