Problema
(A partir da 3ª série do E. M.- Nível de dificuldade: Difícil)
Quantos pares ordenados [tex] (x,y)[/tex], com [tex]x[/tex] e [tex]y[/tex] números reais, satisfazem a equação [tex]\,\boxed{\,x^2+y^2=|x|+|y|\,}\,[/tex]?
E se [tex]x[/tex] e [tex]y[/tex] forem inteiros?
Adaptado do 6º Campeonato de Matemática de la Universidad de La Frontera, 2013.
Ajuda
Equação da circunferência
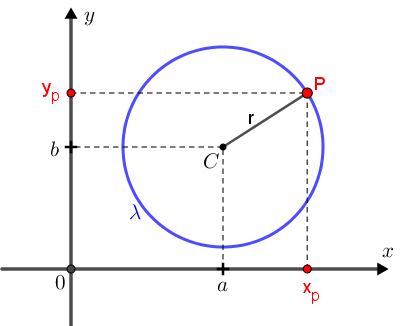
Se, em um plano cartesiano [tex]xOy[/tex], o centro [tex]C[/tex] de uma circunferência [tex]\lambda[/tex] de raio [tex]r[/tex] tem coordenadas [tex](a,b)[/tex], então essa circunferência é definida algebricamente pela equação
- [tex]\lambda:\,\left(x-a\right)^2+\left(y-b\right)^2 =r^2[/tex].
Assim,
[tex]\qquad \boxed{P=(x_p,y_p) \in \lambda \iff \left(x_p-a\right)^2+\left(y_p-b\right)^2 =r^2}[/tex].
Solução
Sejam [tex]x[/tex] e [tex]y[/tex] números reais tais que [tex]\,x^2+y^2=|x|+|y|\,.[/tex]
Vamos dividir a nossa discussão em quatro casos: [tex]\boxed{x \geqslant 0 \text{ e } y \geqslant 0}[/tex]; [tex]\boxed{x \leqslant 0 \text{ e } y \leqslant 0}[/tex]; [tex]\boxed{x \geqslant 0 \text{ e } y \leqslant 0}\,[/tex] e [tex]\,\boxed{x \leqslant 0 \text{ e } y \geqslant 0}\,.[/tex]
Para facilitar a análise da expressão [tex]\,x^2+y^2=x+y[/tex], vamos fazer dois processos de completamento de quadrado.
(Se você não se lembra desse procedimento, dê uma passadinha nesta Sala de Leitura.)
Observe:[tex]\qquad x^2+y^2=x+y\\
\qquad \left(x^2-x\right)+\left(y^2-y\right)=0\\
\qquad \left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}+\left(y-\dfrac{1}{2}\right)^2-\dfrac{1}{4}=0\\
\qquad \left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\dfrac{2}{4}\\
\qquad \left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\left(\dfrac{1}{\sqrt{2}}\right)^2\,.[/tex]
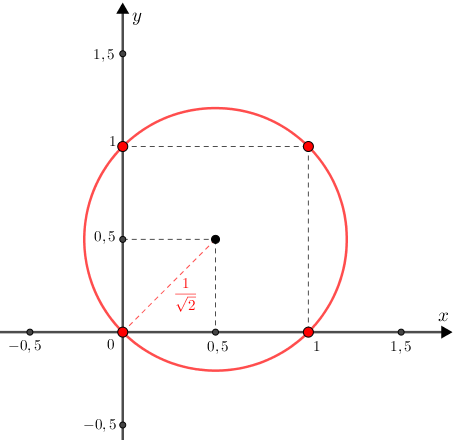
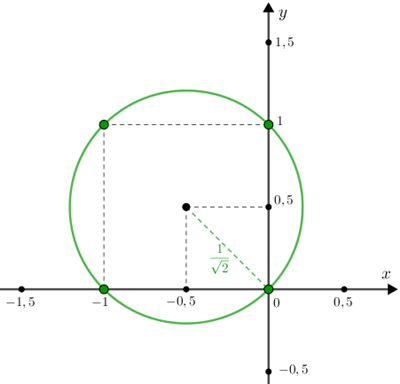
Assim, se os números reais não negativos [tex]x[/tex] e [tex]y[/tex] satisfazem a equação [tex]\,x^2+y^2=|x|+|y|[/tex], então o ponto [tex]P=(x,y)[/tex] é ponto da circunferência do plano cartesiano [tex]xOy[/tex] com centro no ponto [tex]C=\left(\dfrac{1}{2},\dfrac{1}{2}\right)[/tex] e raio [tex]r=\dfrac{1}{\sqrt{2}}:[/tex]
[tex]\qquad \textcolor{red}{\lambda_1: \left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\left(\dfrac{1}{\sqrt{2}}\right)^2}.[/tex]
- Observe que esta primeira análise já nos fornece a resposta da pergunta sobre quantos pares ordenados de números reais satisfazem a equação dada no problema, visto que as coordenadas [tex](x,y)[/tex] de cada ponto da circunferência [tex]\textcolor{red}{\lambda_1}[/tex] satisfazem a equação [tex]\,x^2+y^2=|x|+|y|[/tex] e temos infinitos pontos nessa circunferência.
- Note que temos quatro pontos de [tex]\textcolor{red}{\lambda_1}[/tex] com ambas as coordenadas inteiras: [tex]\textcolor{red}{(0,0)}[/tex], [tex]\textcolor{red}{(1,0)}[/tex], [tex]\textcolor{red}{(1,1)}[/tex] e [tex]\textcolor{red}{(0,1)}\,.[/tex]
Repetindo o processo de completamento de quadrado para os três outros casos, obteremos mais três circunferências cujas coordenadas [tex](x,y)[/tex] de seus respectivos pontos são soluções da equação [tex]x^2+y^2=|x|+|y|[/tex]. Em cada um dos três casos, vamos dar destaque para os pontos que têm coordenadas inteiras, para concluir a solução do problema.
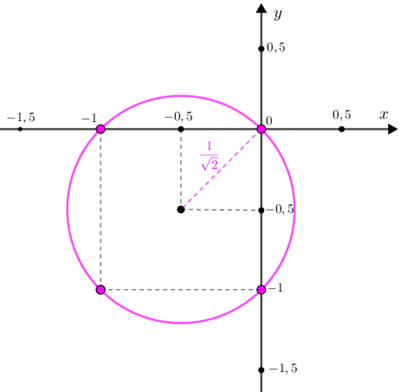
[tex]\textcolor{#800000}{(ii)}[/tex] Se [tex]x \leqslant 0 \,\text{ e }\, y \leqslant 0[/tex], então, da igualdade dada, segue que [tex]\,x^2+y^2=-x-y\,.[/tex] Após dois processos de completamento de quadrado obtemos a equação:[tex] \qquad \left(x+\dfrac{1}{2}\right)^2+\left(y+\dfrac{1}{2}\right)^2=\left(\dfrac{1}{\sqrt{2}}\right)^2[/tex]
e, portanto, concluímos que os números reais não positivos [tex]x[/tex] e [tex]y[/tex] que satisfazem a equação [tex]\,x^2+y^2=|x|+|y|[/tex] definem pontos da circunferência do plano cartesiano [tex]xOy[/tex] com centro no ponto [tex]C=\left(-\dfrac{1}{2},-\dfrac{1}{2}\right)[/tex] e raio [tex]r=\dfrac{1}{\sqrt{2}}:[/tex]
[tex]\qquad \textcolor{#FF00FF}{\lambda_2: \left(x+\dfrac{1}{2}\right)^2+\left(y+\dfrac{1}{2}\right)^2=\left(\dfrac{1}{\sqrt{2}}\right)^2}.[/tex]
- Embora não seja nosso foco no momento, temos infinitos pontos da circunferência [tex]\textcolor{#FF00FF}{\lambda_2}[/tex] cujas coordenadas [tex](x,y)[/tex] satisfazem a equação [tex]\,x^2+y^2=|x|+|y|\,.[/tex]
- Observe que temos mais três pontos com ambas as coordenadas inteiras: [tex]\textcolor{#FF00FF}{(-1,0)}[/tex], [tex]\textcolor{#FF00FF}{(-1,-1)}[/tex] e [tex]\textcolor{#FF00FF}{(0,-1)}\,.[/tex]
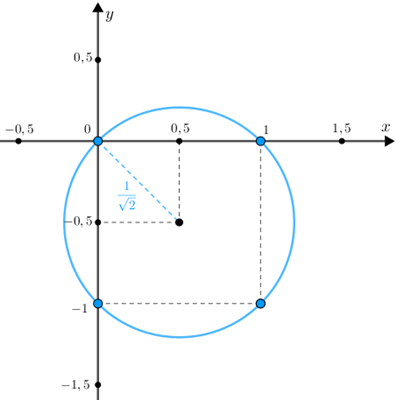
[tex]\textcolor{#800000}{(iii)}[/tex] Considerando agora [tex]x \geqslant 0 \,\text{ e }\, y \leqslant 0[/tex], da igualdade dada segue que [tex]\,x^2+y^2=x-y\,.[/tex] Após mais dois processos de completamento de quadrado obtemos:[tex] \qquad \left(x-\dfrac{1}{2}\right)^2+\left(y+\dfrac{1}{2}\right)^2=\left(\dfrac{1}{\sqrt{2}}\right)^2[/tex]
e, portanto, neste caso, os números reais [tex]x[/tex] e [tex]y[/tex] que satisfazem a equação [tex]\,x^2+y^2=|x|+|y|[/tex] definem pontos da circunferência do plano cartesiano [tex]xOy[/tex] com centro no ponto [tex]C=\left(\dfrac{1}{2},-\dfrac{1}{2}\right)[/tex] e raio [tex]r=\dfrac{1}{\sqrt{2}}\,:[/tex]
[tex]\qquad \textcolor{#0099FF}{\lambda_3: \left(x-\dfrac{1}{2}\right)^2+\left(y+\dfrac{1}{2}\right)^2=\left(\dfrac{1}{\sqrt{2}}\right)^2}.[/tex]
- Aqui também temos infinitos pontos da circunferência
cujas coordenadas [tex](x,y)[/tex] satisfazem a equação [tex]\,x^2+y^2=|x|+|y|\,.[/tex] - Veja que em [tex]\textcolor{#0099FF}{\lambda_3}[/tex] conseguimos mais um ponto com ambas as coordenadas inteiras diferentes dos que já temos: [tex]\textcolor{#0099FF}{(1,-1)}.[/tex]
[tex]\textcolor{#800000}{(iv)}[/tex] Considerando, para terminar as análises, [tex]x \leqslant 0 \,\text{ e }\, y \geqslant 0[/tex], da igualdade do problema segue que [tex]\,x^2+y^2=-x+y\,.[/tex] Após mais dois processos de completamento de quadrado obtemos:[tex] \qquad \left(x+\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\left(\dfrac{1}{\sqrt{2}}\right)^2[/tex]
e, portanto, os números reais [tex]x[/tex] e [tex]y[/tex] que neste caso satisfazem a equação [tex]\,x^2+y^2=|x|+|y|[/tex] definem pontos da circunferência do plano cartesiano [tex]xOy[/tex] com centro no ponto [tex]C=\left(-\dfrac{1}{2},\dfrac{1}{2}\right)[/tex] e raio [tex]r=\dfrac{1}{\sqrt{2}}:[/tex]
[tex]\qquad \textcolor{#009900}{\lambda_4: \left(x+\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\left(\dfrac{1}{\sqrt{2}}\right)^2}.[/tex]
- Aqui também temos infinitos pontos da circunferência [tex]\textcolor{#009900}{\lambda_4}[/tex] cujas coordenadas [tex](x,y)[/tex] satisfazem a equação [tex]\,x^2+y^2=|x|+|y|\,.[/tex]
- Em [tex]\textcolor{#009900}{\lambda_4}[/tex] conseguimos mais um ponto com ambas as coordenadas inteiras, diferente dos exibidos:[tex]\textcolor{#009900}{(-1,1)}.[/tex]
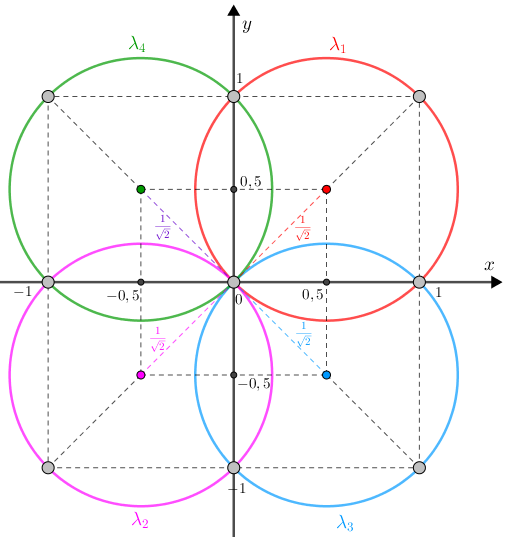
Logo, temos [tex]\,\fcolorbox{black}{#eee0e5}{$\text{infinitos}$}\,[/tex]pares ordenados [tex] (x,y)[/tex] de números reais que satisfazem a equação [tex]\,x^2+y^2=|x|+|y|[/tex], de acordo com as análises feitas e com a figura mostrada abaixo. Particularmente temos [tex]\,\fcolorbox{black}{#eee0e5}{$\text{nove}$}\,[/tex] desses infinitos pontos com ambas as coordenadas definidas por números inteiros: [tex]\textcolor{#969696}{(0,0)}[/tex], [tex]\textcolor{#969696}{(1,0)}[/tex], [tex]\textcolor{#969696}{(1,1)}[/tex], [tex]\textcolor{#969696}{(0,1)}[/tex], [tex]\textcolor{#969696}{(-1,1)}[/tex], [tex]\textcolor{#969696}{(-1,0)}[/tex], [tex]\textcolor{#969696}{(-1,-1)}[/tex], [tex]\textcolor{#969696}{(0,-1)}[/tex], [tex]\textcolor{#969696}{(1,-1)}.[/tex]
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |