Dedução 4
Aqui, utilizaremos três Lemas para mais uma dedução da fórmula de Herão:
– o segundo Lema nos fornecerá a figura que servirá de base para essa dedução;
– o primeiro Lema é uma propriedade sobre retas tangentes a uma dada circunferência, a qual utilizaremos fortemente para provarmos o segundo Lema;
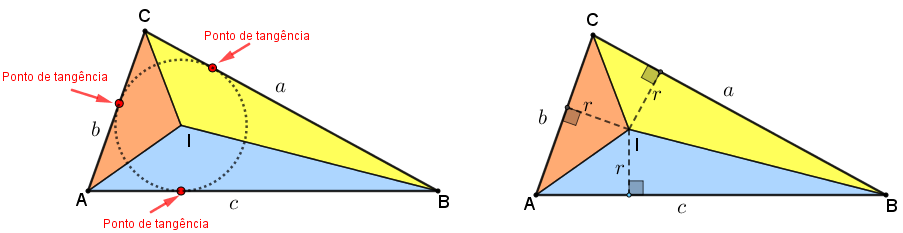
– o terceiro Lema já apareceu na Dedução 2 e relaciona a área de um triângulo com o raio da sua circunferência inscrita e seu semiperímetro.
Os fatos elementares da Geometria Plana que utilizaremos serão apenas citados.
Os Lemas
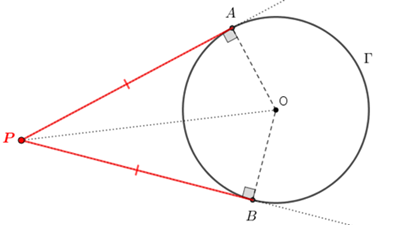
✐ Lema 1: Se, a partir de um ponto [tex]P[/tex] externo a uma circunferência [tex]\Gamma[/tex], traçarmos as retas [tex]PA[/tex] e [tex]PB[/tex] tangentes a [tex]\Gamma[/tex], com [tex]A[/tex] e [tex]B[/tex] pontos de [tex]\Gamma[/tex], então os segmentos [tex]\overline{PA}[/tex] e [tex]\overline{PB}[/tex] terão o mesmo comprimento.
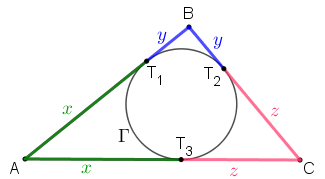
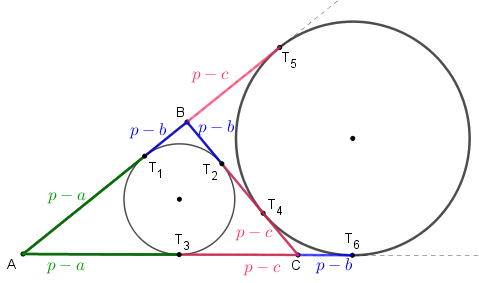
✐ Lema 2: Seja [tex]ABC[/tex] um triângulo cujos lados [tex]AB\, [/tex], [tex]BC\, [/tex] e [tex]\, CA[/tex] têm comprimentos [tex]c\, ,\, a\, , b\, [/tex], respectivamente.
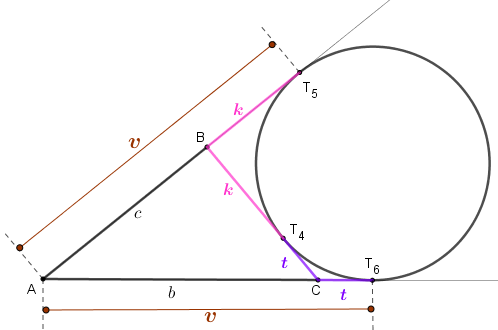
Se [tex]T_1\, , \, T_2\, ,\, T_3\, [/tex] são os pontos de tangência da circunferência inscrita ao triângulo [tex]ABC\, [/tex]; [tex]T_4\, , \, T_5\, ,\, T_6\, [/tex] são os pontos de tangência da circunferência ex-inscrita relativa ao vértice [tex]A[/tex] do triângulo [tex]ABC\, [/tex] e [tex]p=\dfrac{a+b+c}{2}[/tex] é o semiperímetro do triângulo [tex]ABC[/tex], então:
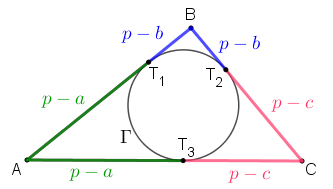
- Os comprimentos dos segmentos [tex]\textcolor{#009900}{AT_1}\, [/tex] e [tex]\, \textcolor{#009900}{AT_3}[/tex] são iguais a [tex]\textcolor{#009900}{p-a}.[/tex]
- Os comprimentos dos segmentos [tex]\textcolor{#0000FF}{BT_1}\, [/tex], [tex]\, \textcolor{#0000FF}{BT_2}\, [/tex] e [tex]\, \textcolor{#0000FF}{CT_6}[/tex] são iguais a [tex]\textcolor{#0000FF}{p-b}.[/tex]
- Os comprimentos dos segmentos [tex]\textcolor{#FF3366}{CT_2}\, [/tex], [tex]\, \textcolor{#FF3366}{CT_3}\, [/tex] e [tex]\, \textcolor{#FF3366}{BT_5}[/tex] são iguais a [tex]\textcolor{#FF3366}{p-c}.[/tex]
A dedução
Seja [tex]ABC[/tex] um triângulo cujos lados [tex]\overline{AB}\, [/tex], [tex]\overline{BC}\, [/tex] e [tex]\, \overline{CA}[/tex] têm comprimentos [tex]c\, ,\, a\, , b\, [/tex], respectivamente.
Considere que [tex]T_1\, , \, T_2\, ,\, T_3\, [/tex] são os pontos de tangência da circunferência inscrita ao triângulo [tex]ABC\, [/tex]; [tex] \, T_5\, ,\, T_6\, [/tex] são os pontos de tangência da circunferência ex-inscrita relativa ao vértice [tex]A[/tex] do triângulo [tex]ABC\, [/tex] e [tex]p=\dfrac{a+b+c}{2}[/tex] é o semiperímetro do triângulo [tex]ABC[/tex].
De acordo com o Lema 2, os valores [tex]a,b,c,p[/tex] definem as medidas dos vários segmentos que aparecem na figura a seguir. Observe que denotamos por [tex]I[/tex] e [tex]I_A[/tex] os centros das circunferências inscrita e ex-inscrita, respectivamente.
(Embora tenha sido importante para a justificativa do Lema 2, não trabalharemos com o ponto de tangência [tex] \, T_4\, [/tex] nesta dedução.)
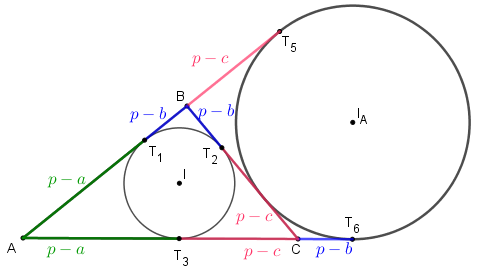
Vamos utilizar os dados da figura acima para analisar os triângulos [tex]AT_5I_A[/tex], [tex]AT_1I[/tex], [tex]IT_3C[/tex], e [tex]I_AT_6C[/tex].
Na figura à direita, vamos denotar por [tex]r\, [/tex] e [tex]\, R\, [/tex] os raios das circunferências inscrita e ex-inscrita, respectivamente. É sempre bom lembrar-se de que, como o ex-incentro [tex]I_A[/tex] é ponto da bissetriz interna do ângulo de vértice [tex]A[/tex], então os pontos [tex]A[/tex], [tex]I[/tex] e [tex]I_A[/tex] são colineares, o que possibilita a análise via semelhança que faremos a seguir.
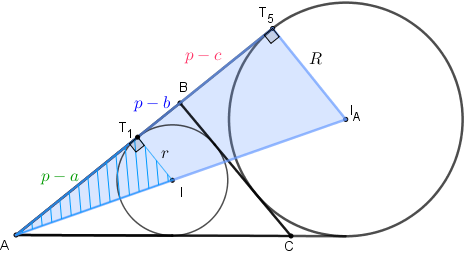
- Observe que os triângulos [tex]AT_5I_A[/tex] e [tex]AT_1I[/tex] são semelhantes, pois têm um ângulo reto cada um e o ângulo de vértice [tex]A[/tex] em comum.
Dessa forma, lados correspondentes desses dois triângulos são proporcionais e, assim:
[tex]\qquad \dfrac{r}{R}= \dfrac{p-a}{(p-a)+(p-b)+(p-c)}\, [/tex],
donde segue que:
[tex]\qquad \dfrac{r}{R}= \dfrac{p-a}{3p-(a+b+c)}\\
\qquad R\cdot(p-a)= r \cdot (3p-(a+b+c))\\
\qquad R\cdot(p-a)= r \cdot \left(3\cdot \dfrac{a+b+c}{2}-(a+b+c)\right)\\
\qquad R\cdot(p-a)= r \cdot \left(\dfrac{3\cdot(a+b+c)-2\cdot(a+b+c)}{2}\right)\\
\qquad R\cdot(p-a)= r \cdot \left(\dfrac{a+b+c}{2}\right)\\
\qquad R\cdot(p-a)= r \cdot p.\qquad \textcolor{#800000}{(*)}\\
[/tex]
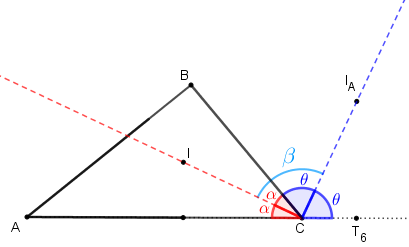
Antes de analisarmos os triângulos [tex]IT_3C[/tex], e [tex]I_AT_6C[/tex], vamos estabelecer uma propriedade que ajudará nessa análise. Para isso, vamos introduzir dois objetos matemáticos novos na discussão: os segmentos [tex]\overline{CI}\, [/tex] e [tex]\, \overline{CI_A}[/tex].
A partir dessas informações, vamos obter a medida [tex]\beta[/tex], em graus, do ângulo [tex]I_A\hat{C}I.[/tex] Para tal, perceba que os ângulos [tex]T_6\hat{C}B[/tex] e [tex]B\hat{C}A[/tex] são suplementares, logo [tex]2 \alpha+2\theta=180^\circ[/tex] e, portanto, [tex] \alpha+\theta=90^\circ[/tex], ou seja, [tex]\beta=90^\circ.[/tex]
- Agora sim, observe os triângulos [tex]IT_3C[/tex] e [tex]I_AT_6C[/tex]. Inicialmente perceba que, de acordo com a notação da figura abaixo, à esquerda, temos que:
[tex]\quad \alpha+90^\circ+\theta= 180^\circ\\
\quad \alpha+\theta= 90^\circ\, .\quad \textcolor{#800000}{(i)}[/tex][tex]\quad \alpha+90^\circ+\alpha_1= 180^\circ\\
\quad \alpha+\alpha_1= 90^\circ\, .\quad \textcolor{#800000}{(ii)}[/tex][tex]\quad \theta+90^\circ+\theta_1= 180^\circ\\
\quad \theta+\theta_1= 90^\circ\, .\quad \textcolor{#800000}{(iii)}[/tex]Note que:
- de [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], concluímos que [tex] \alpha+\theta= \alpha+\alpha_1[/tex] e, portanto, [tex] \boxed{\theta= \alpha_1\, }\, [/tex];
- de [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], concluímos que [tex] \alpha+\theta= \theta+\theta_1[/tex] e, portanto, [tex] \boxed{\alpha= \theta_1\, }\, [/tex];
e, assim, obtemos a figura abaixo, à direita.
Essa figura nos mostra que os triângulos [tex]IT_3C[/tex], e [tex]I_AT_6C[/tex] também são semelhantes.
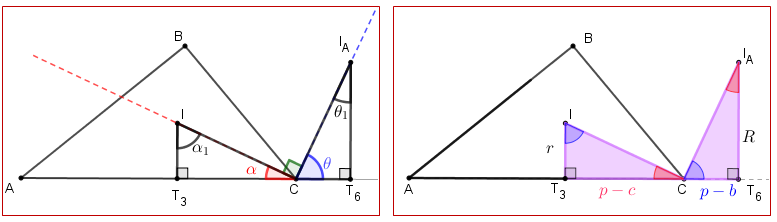
Da semelhança dos triângulos [tex]IT_3C[/tex], e [tex]I_AT_6C[/tex] vem que:
[tex]\qquad \dfrac{r}{p-b}= \dfrac{p-c}{R}\, [/tex],
donde segue que:
[tex]\qquad r\cdot R= (p-c) \cdot (p-b)\\
\qquad R=\dfrac{(p-b) \cdot (p-c)}{r}.\qquad \textcolor{#800000}{(**)}\\
[/tex]
Substituindo [tex]\textcolor{#800000}{(**)}[/tex] em [tex]\textcolor{#800000}{(*)}[/tex], obtemos que:
[tex]\qquad R\cdot(p-a)= r \cdot p\\
\qquad \dfrac{(p-b) \cdot (p-c)}{r}\cdot(p-a)= r \cdot p\\
\qquad \dfrac{(p-b) \cdot (p-c)\cdot(p-a)}{p}= r^2 \\
\qquad r=\pm \sqrt{ \dfrac{(p-b) \cdot (p-c)\cdot(p-a)}{p}}. \\
[/tex]
e, como [tex]r[/tex] é uma medida, [tex]r \gt 0[/tex]; logo, [tex]r=\sqrt{ \dfrac{(p-b) \cdot (p-c)\cdot(p-a)}{p}}.[/tex]
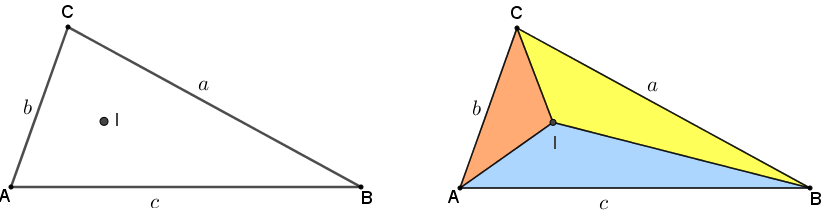
Finalmente, pelo Lema 3, se [tex]A_t[/tex] é a área do triângulo [tex]ABC[/tex], então [tex]A_t=r\cdot p[/tex]; portanto:
[tex]\qquad A_t=\sqrt{ \dfrac{(p-b) \cdot (p-c)\cdot(p-a)}{p}}\cdot p\\
\qquad A_t=\sqrt{ \dfrac{p\cdot (p-b) \cdot (p-c)\cdot(p-a)}{p^2}}\cdot p \quad (\text{Lembre que } p \gt 0.)\\
\qquad A_t=\sqrt{ p\cdot (p-b) \cdot (p-c)\cdot(p-a)}\cdot \dfrac{\cancel{p}}{\cancel{p}}\\
\qquad \, \fcolorbox{black}{#eee5de}{$A_t=\sqrt{p\, (p-a)\, (p-c)\, (p-b)}$}\, .[/tex]
 |
Se necessário, visite a Sala de Leitura Circunferências ex-inscritas. |
Equipe COM – OBMEP