|
O que vamos fazer aqui? |
 |
 |
Que bom que você entendeu esse importante resultado da geometria! |
Soma dos ângulos internos de um triângulo – um pouco mais . . .
Problemas
Problema 1: Sejam A, B e C pontos não colineares e considere o triângulo definido por esses pontos.
Seja r a reta que passa por C e é paralela ao segmento definido por A e B e sejam α, β, γ, α’, β’ e γ’ as medidas dos ângulos indicadas na figura.
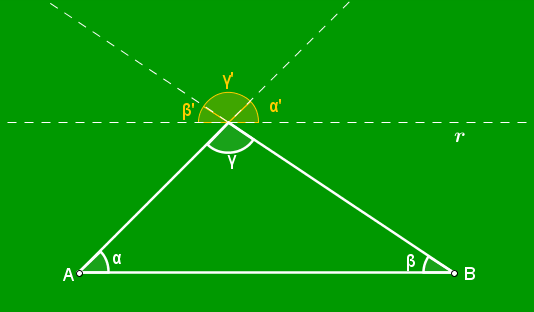
Justifique as afirmações abaixo.
Afirmação 1: α = α’
Afirmação 2: β = β’
Afirmação 3: γ = γ’
Problema 2: Determine, em graus, a medida α indicada na figura abaixo.
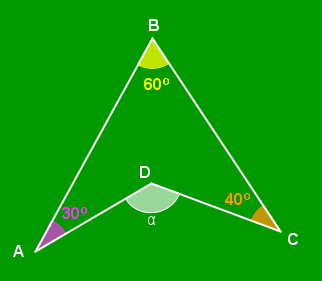
Problema 3: Determine, em graus, a soma das medidas dos ângulos externos de um triângulo (um por vértice).
Se você não se lembra do que é um ângulo externo de um triângulo, vamos reescrever o enunciado do problema:
Determine, em graus, [tex]\lambda+\theta+\varphi[/tex], sabendo que [tex]\lambda,\, \theta,\, \varphi[/tex] são as medidas indicadas na figura abaixo.
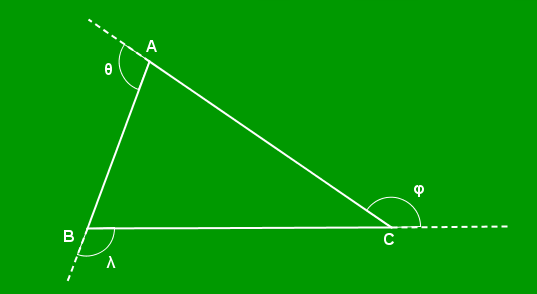
|
Não faço a menor ideia de quanto é a soma das medidas dos ângulos externos de um triângulo! |
 |
 |
Utilize os applets abaixo, observe situações particulares e tente estabelecer um padrão para a resposta do problema. Depois, tente mostrar que a sua resposta está certa, fazendo uma pequena demonstração. |
Applets
No gif animado abaixo, podemos ver alguns triângulos e as respectivas medidas de seus ângulos externos.
Depois de observar alguns exemplos, tente estabelecer uma relação genérica entre as medidas obtidas.
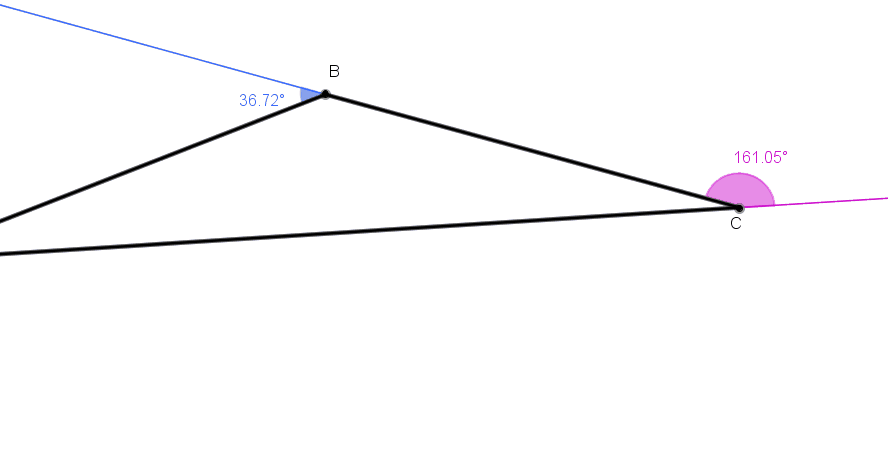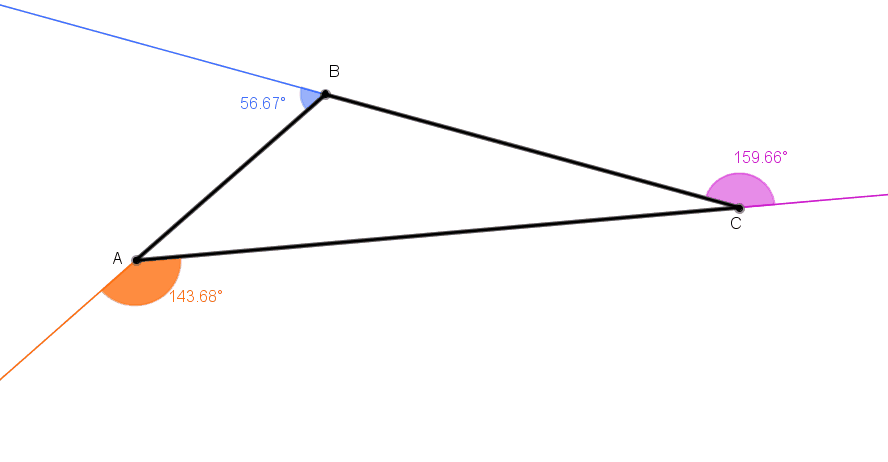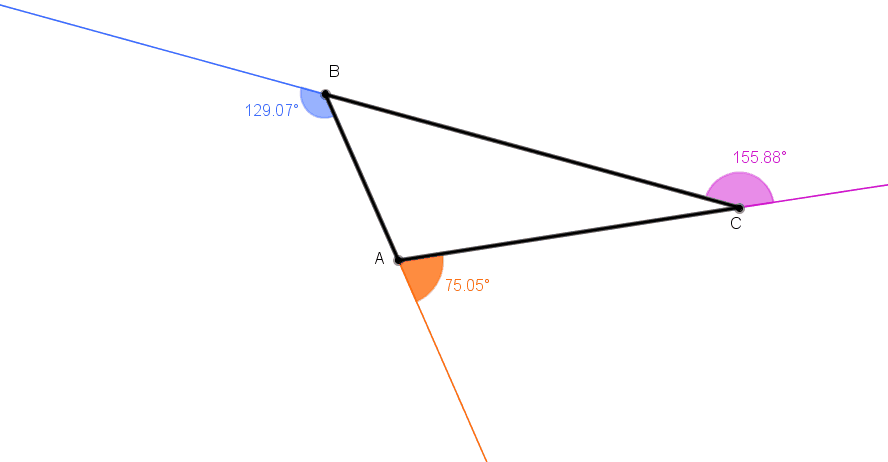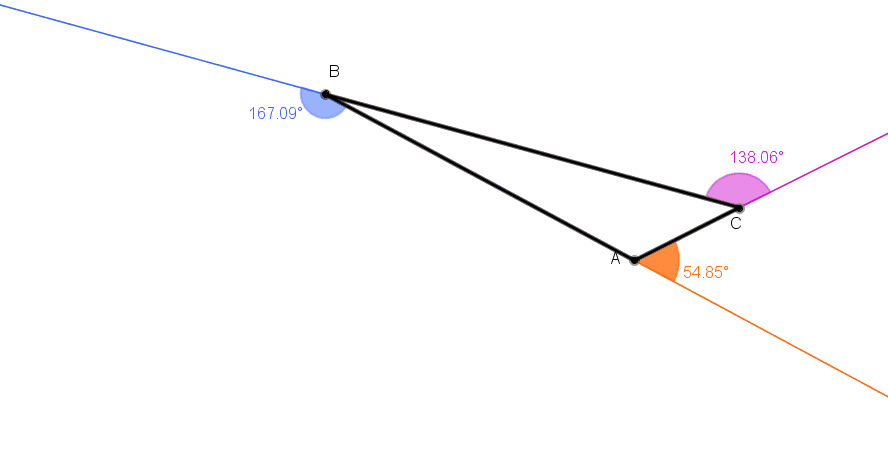
OBMEP_ srdg, criado com o GeoGebra
Neste gif animado aparecem os mesmos triângulos que aparecem no gif anterior.
No entanto, a velocidade da animação neste segundo gif permitirá que você o utilize para fazer as anotações necessárias para as suas observações.
Lembre-se de que o GeoGebra fornece valores aproximados para as medidas apresentadas.
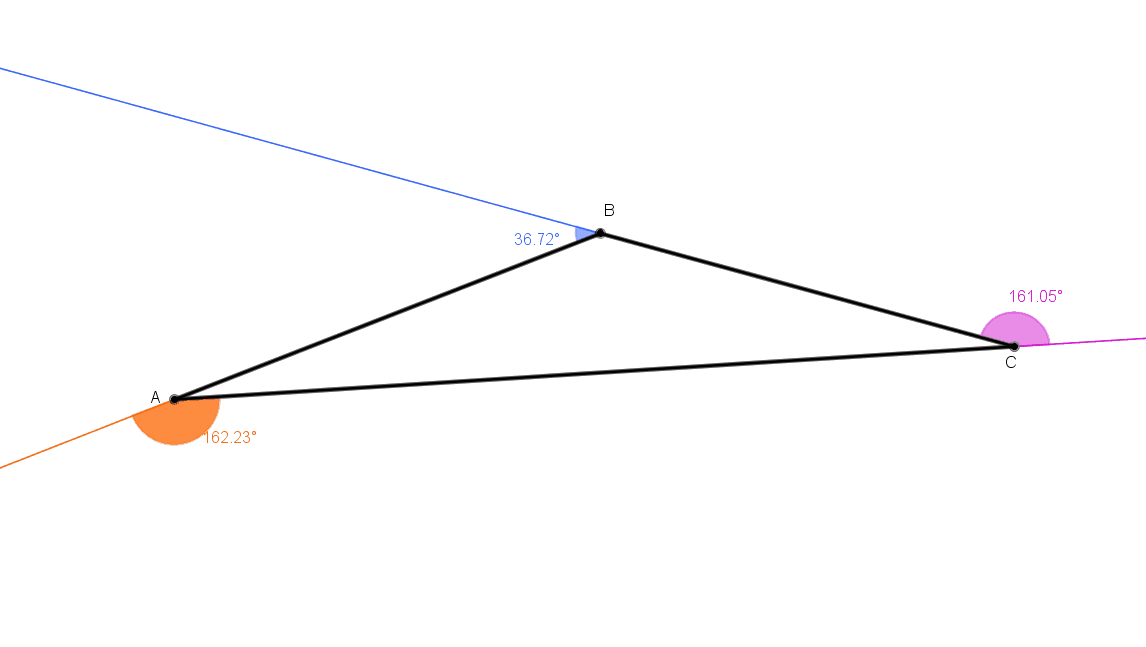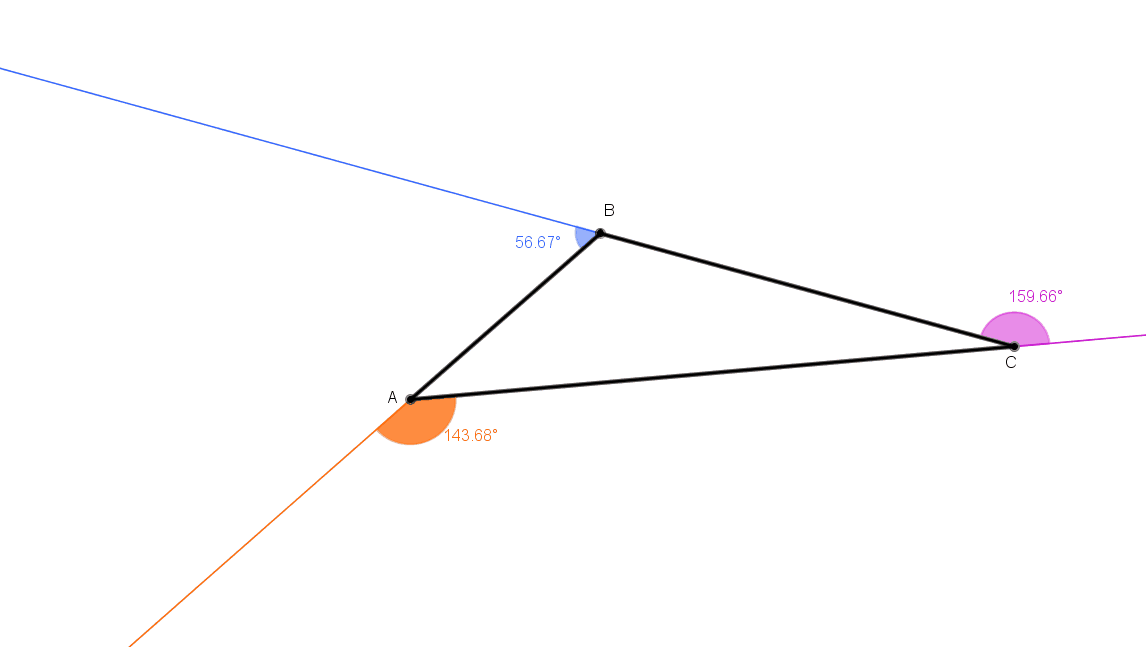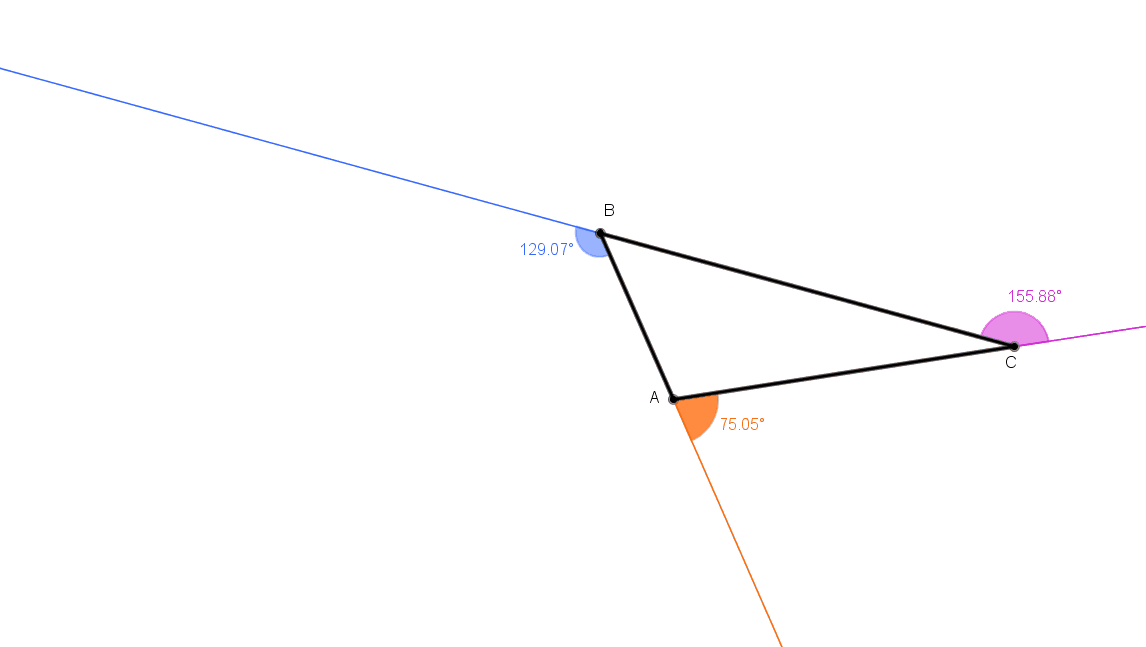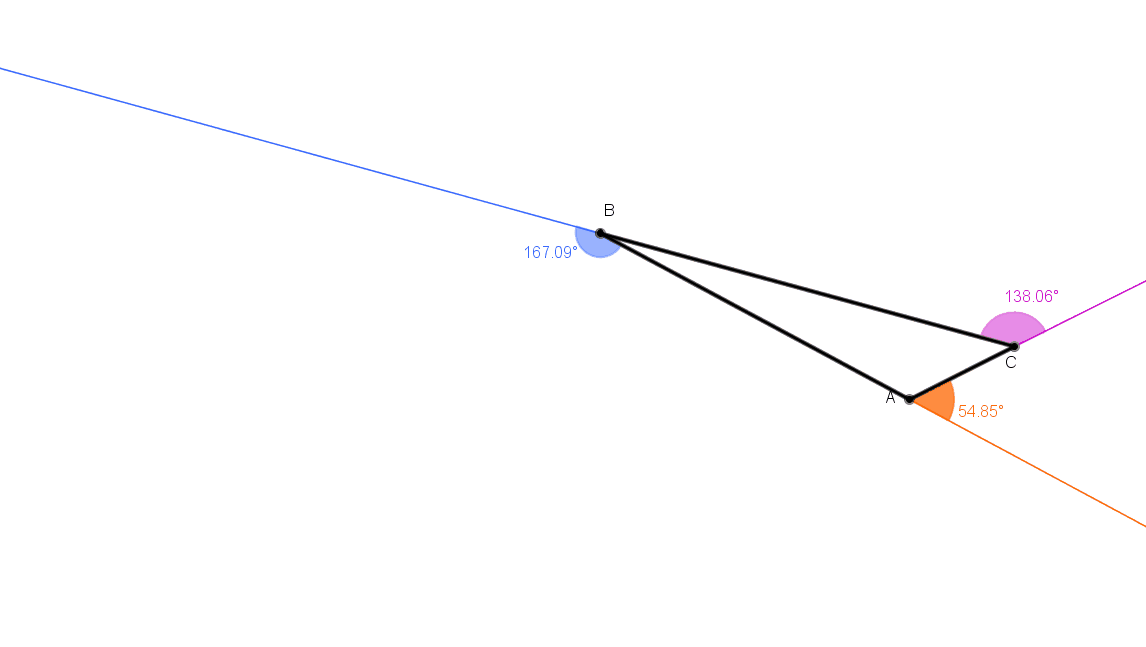
OBMEP_ srdg, criado com o GeoGebra
 |
Ainda com dificuldades? |
Equipe COM – OBMEP
Voltar para a Sala de Estudos sobre a soma dos ângulos internos de um triângulo.
