Aplicando a matemática básica – Sala 2

As frações da música

Desde a antiguidade, os matemáticos utilizavam razões e médias na construção de escalas musicais e, nos dias de hoje, qualquer pessoa que estude teoria musical verá que a relação entre Música e Matemática vai além da letra M do início dessas duas palavras.
Nesta sala, particularmente, vamos mostrar algumas relações existentes entre, quem diria, notas e frações.

Fiquem com a gente e aproveitem…

O nome dessa música é Hurrian Hymn. Ela tem cerca de 3,4 mil anos e é considerada a mais antiga música do mundo! A canção, dedicada à deusa Nikkal, foi descoberta por volta de 1950, durante escavações arqueológicas na região da antiga cidade de Ugarit, hoje parte da Síria.

Mas se as civilizações antigas não conheciam o processo de gravação de músicas, como essa música chegou até os dias de hoje? Como ela foi encontrada???

Nas civilizações antigas, antes do surgimento da escrita, mensageiros eram encarregados de transmitir as notícias oralmente, viajando a pé, de barco ou a cavalo. Claramente, não demorou até que o homem percebesse a importância da comunicação escrita e podemos afirmar, sem sombra de dúvida, que o surgimento da escrita foi, e ainda é, um dos maiores pilares do progresso da humanidade. Com a durabilidade de sinais grafados foi possível atravessar a barreira do tempo e trazer para os dias de hoje o modo de vida daqueles que viveram em locais e tempos muito distantes. Mas essa escrita na qual vocês estão pensando não permitia preservar a música, que, também, por muito tempo foi transmitida oralmente de uma pessoa para outra até a invenção de uma “escrita musical”. E, diferentemente do que ocorreu com a “escrita das palavras”, que depende da língua na qual se escreve, nos dias de hoje a “escrita musical” é universal e, portanto, compreendida em qualquer língua!
Particularmente, a Hurrian Hymn que vocês ouviram não foi encontrada escrita na linguagem musical universal utilizada atualmente: a peça foi escrita em uma linguagem antiga e foi cunhada em placas de argila. Depois de encontrado, o material foi estudado e, após 15 anos de pesquisa, a professora Anne Kilmer (da Universidade da Califórnia) fez a tradução moderna da “escrita das palavras” e da “escrita da música” do que hoje é considerado o achado musical mais antigo conhecido no mundo!
E é na definição de uma importante ferramenta de comunicação entre músicos de todo o mundo que a matemática, especialmente as frações, se faz presente. Então, vamos lá!

A escrita musical é muito importante no processo de se transmitir uma música da maneira em que esta foi concebida; e, dentre as várias maneiras de se escrever música, a mais usada é a partitura. Tal como qualquer sistema de escrita, a partitura dispõe de símbolos próprios (as notas musicais) aos quais se associam os sons. Traduzindo em miúdos, a partitura é, simplesmente, o registro de sons no papel.
Mas para que as notas possam descrever corretamente uma música, elas dependem de outros símbolos. Assim, uma partitura é composta de notas, compassos, pentagramas e claves.

► O pentagrama (ou pauta) é um conjunto de cinco linhas paralelas e equidistantes e os quatro espaços entre elas. É a base sobre a qual as notas musicais serão escritas: as notas podem ser representadas tanto em cima das linhas como nos espaços entre elas.

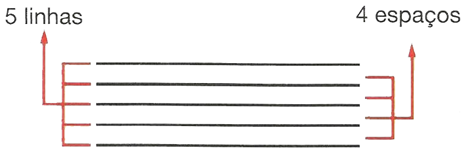
Linhas e espaços são numerados de baixo para cima.

► O elemento básico de um sistema de notação musical é a nota e cada nota representa um som. Existem sete notas musicais – Dó, Ré, Mi, Fá, Sol, Lá e Si – e cada nota tem duas características básicas: sua duração e sua altura. Essas duas características determinam como cada nota deve ser representada na pauta:
– a duração de um som é indicada pela figura que utilizamos para desenhar a nota associada a esse som;
– a altura de cada nota fica determinada pela posição que a figura que a representa é desenhada no pentagrama.
Vejamos, então, como cada nota é representada na pauta.
Como observamos, para desenhar as notas no pentagrama utilizamos símbolos para representar a duração dos respectivos sons. Atualmente, a semibreve (uma bola branca) é a figura que representa o som de maior duração. Uma vez definida a duração da semibreve em uma música (por exemplo, 4 segundos), as demais figuras serão frações desta. Observem a próxima tabela, nela podemos ver os símbolos atualmente utilizados para representar a duração das notas, o nome de cada símbolo e a respectiva duração do som associado ao símbolo.

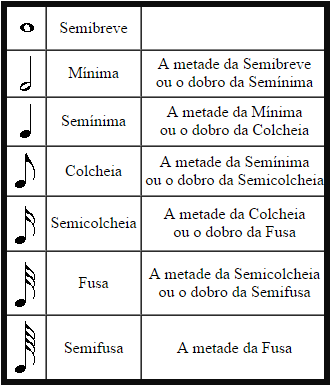
Tabela 1: Equivalência dos tempos de duração.

Dessa forma, se [tex]t[/tex] é a duração, digamos em segundos, da semibreve em uma música, então as frações correspondentes à duração das demais figuras podem ser visualizadas abaixo.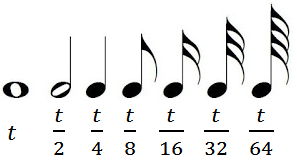

Logo, em tempo de duração, uma semibreve é equivalente a duas mínimas, a quatro semínimas, a oito colcheias e assim sucessivamente, conforme mostra a figura abaixo.

► Também observamos que a posição de uma nota no pentagrama indica a altura do som a ela associado. Mesmo que seja estabelecido que “quanto mais em cima a nota for grafada na pauta, mais agudo será o som que ela representa”, apenas os símbolos que identificam tempo de duração não são suficientes para representarmos as notas na pauta. Precisamos relacionar de maneira precisa a posição de cada nota no pentagrama com a sua respectiva altura. Para essa identificação, utilizamos mais um elemento gráfico: a clave. Claves servem, então, para aquilo que os músicos chamam de identificar a altura da nota (identificar se é mais grave ou mais aguda) e também para dar nome às notas no pentagrama, já que os nomes Dó, Ré, Mi, Fá, Sol, Lá, Si estão de alguma forma ligados às alturas musicais.
Atualmente temos três tipos de claves: clave de Dó, clave de Fá e clave de Sol. As mais utilizadas são as claves de Sol e de Fá na 4ª linha. Cada uma delas é representada por símbolos que são grafados no início dos pentagramas, conforme mostra a figura abaixo.

A identificação das notas a partir dessas duas claves fica assim definida:

– uma vez escrita a Clave de Sol em um pentagrama, ela indica que a nota escrita sobre a segunda linha é um Sol;
– uma vez escrita a Clave de Fá na 4ª linha num pentagrama, ela indica que a nota escrita sobre a quarta linha é um Fá.

Fixada a Clave de Sol ou a Clave de Fá na 4ª linha, sabemos onde está o Sol ou onde está o Fá no pentagrama, assim podemos registrar as demais notas de acordo com a clave escolhida:

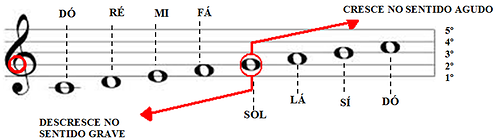
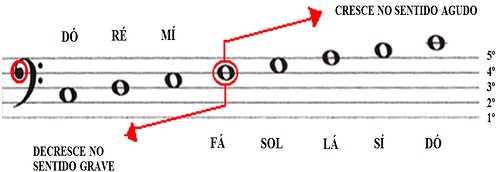
Assim, dependendo da clave utilizada, a leitura dos nomes das notas é diferente. Comparem os nomes das semibreves desenhadas nos pentagramas abaixo, de acordo com as respectivas claves:

► Como vimos, para estruturar a escrita de uma música utilizamos figuras musicais que são dispostas graficamente em uma pauta. Para que a leitura dessas figuras possa ser feita de maneira compreensível e de modo a dar ritmo na execução da música, utilizamos um importante elemento que organiza a grafia das figuras musicais no pentagrama: o compasso. De maneira simplista, chamamos de compasso cada uma das divisões dos sons de uma música em intervalos de mesma duração. Assim, os compassos são unidades musicais compostas por determinadas quantidades de notas e dividem uma música em “agrupamentos musicais” com a mesma duração. Nos pentagramas, cada compasso é fisicamente limitado por barras verticais e a quantidade de determinada figura que pode comparecer em um compasso fica perfeitamente determinada pela chamada fórmula do compasso.
A fórmula de compasso é um símbolo em forma de fração colocado no início de uma pauta, após sua clave.
Fixada uma fórmula de compasso, é possível obter as várias formas dos compassos definidos pela fórmula dada, bastando para isso definirmos um compasso que chamaremos de “forma modelo” e usarmos a Tabela 1 que mostra a equivalência entre os tempos de duração das notas para obter outras formas para o compasso, a partir da forma modelo.
A “forma modelo” será o compasso assim definido:
[tex](i)[/tex] a única figura musical que o compõe é a figura correspondente ao número inferior da fórmula de compasso. (Essa correspondência entre número e figura pode ser visualizada na Tabela 2, abaixo.)
[tex](ii)[/tex] a quantidade da figura indicada pelo número inferior é exatamente o número superior da fórmula.
Dessa forma, com relação ao compasso modelo, a fórmula de compasso deve ser lida como a quantidade de determinada figura que será grafada no compasso.
Vejam, então, a tabelinha que determina a correspondência entre número e figura musical.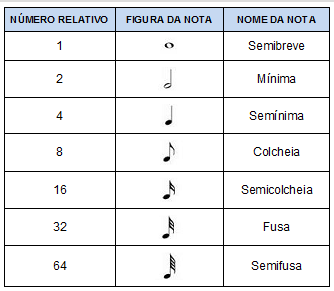

Tabela 2: Número X figura musical.

Para exemplificar, o compasso modelo da fórmula de compasso [tex]3/4[/tex] é formado por três figuras associadas ao número [tex]4,[/tex] ou seja, três semínimas. Vejamos um exemplo mais completo.
Suponhamos que a fórmula de compasso de outra partitura seja [tex]4/4[/tex]. Agora, o compasso modelo terá quatro figuras que correspondem ao número [tex]4[/tex], a semínima, e usando a Tabela 1 de equivalência entre os tempos de duração das figuras musicais observamos, por exemplo, que:
[tex]\qquad \qquad ⇒[/tex] uma mínima equivale a duas semínimas;
[tex]\qquad \qquad ⇒[/tex] uma semibreve equivale a duas mínimas.
Assim, no pentagrama abaixo representamos quatro compassos associados à fórmula [tex]4[/tex] por [tex]4[/tex], utilizando a nota Lá.

Os pitagóricos estão entre os primeiros a observarem as relações existentes entre os números e a natureza. Conta uma lenda que Pitágoras (569 a.C. – 480 a.C., aproximadamente) despertou sua curiosidade em relação à música quando, ao passar em frente à oficina de um ferreiro, ouviu o som de cinco martelos batendo em uma bigorna e percebeu que os martelos soavam harmonicamente, exceto um. Curioso, ele tentou estabelecer uma relação entre os martelos que eram harmônicos: pressupôs algumas possíveis razões, como a força com a qual o martelo era conduzido, e, como não conseguiu encontrar a resposta, decidiu pesar os martelos e percebeu que a massa de cada martelo era de [tex]12, \, 9, \, 8[/tex] e [tex]6[/tex] unidades de peso. Ao observarmos estes números podemos notar que [tex]\boxed{\dfrac{6}{8}=\dfrac{9}{12}} \, \, \, [/tex] e [tex] \, \, \, \boxed{\dfrac{6}{9}=\dfrac{8}{12}}[/tex]. Mais ainda, [tex]9[/tex] é a média aritmética e [tex]8[/tex] a média harmônica de [tex]6[/tex] e [tex]12[/tex], já que [tex]\boxed{9=\dfrac{6+12}{2}} \, \, [/tex] e [tex]\boxed{ \, \, 8=\dfrac{2}{\frac{1}{6}+\frac{1}{12}}}[/tex].
Ainda não satisfeito, Pitágoras fez experimentos observou outras relações entre estes números, como a proporção dos pesos entre si: [tex]\boxed{6=\dfrac{1}{2}\times 12}[/tex]; [tex]\boxed{8=\dfrac{2}{3}\times 12}[/tex] e [tex]\boxed{9=\dfrac{3}{4}\times 12}[/tex].
Para pesquisar os sons correspondentes a essas três últimas relações, Pitágoras teria esticado uma corda que produzia um determinado som e, tomando esse som como fundamental, teria feito marcas na corda, dividindo-a em doze secções iguais. Esse artefato, que seria chamado de monocórdio (mono = um e córdio = corda), podia ser “tocado” com uma espécie de palheta ou vareta enquanto algum objeto, como uma pedra, era deslocado ao longo da corda para produzir sons.

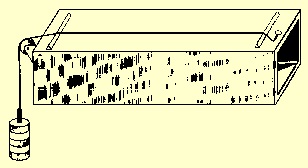
Monocórdio de Pitágoras

A partir das divisões feitas na corda, ele observou que o som produzido pressionando metade da corda era o mesmo, porém mais agudo, que o som produzido pela corda inteira. Analogamente, observou que os sons produzidos pressionando a corda na sexta e na nona marcas combinavam com o som da corda inteira. Ou seja:

– pressionando a corda na sexta marca (correspondente a 1/2 do comprimento da corda), se produzia o que chamamos de oitava do som produzido pela corda solta (inteira);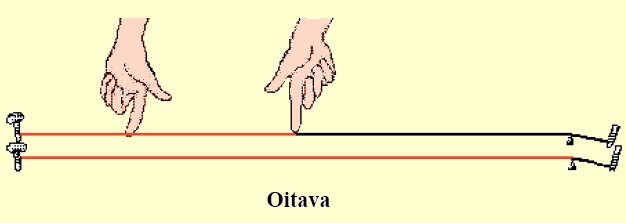
– pressionando a corda na nona marca (correspondente a 3/4 do comprimento da corda), resultava o que chamamos de quarta do som produzido pela corda solta;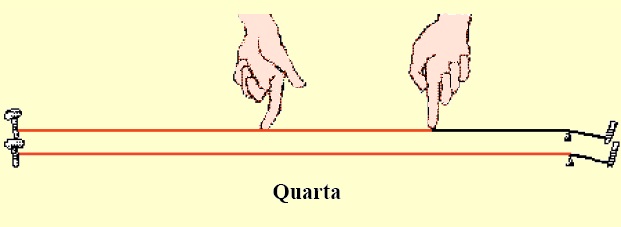
– e pressionando a corda na oitava marca (correspondente a 2/3 do comprimento da corda), resultava o que chamamos de quinta do som produzido pela corda solta.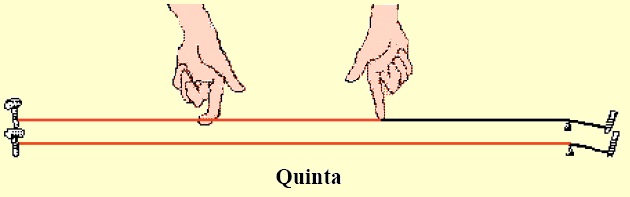

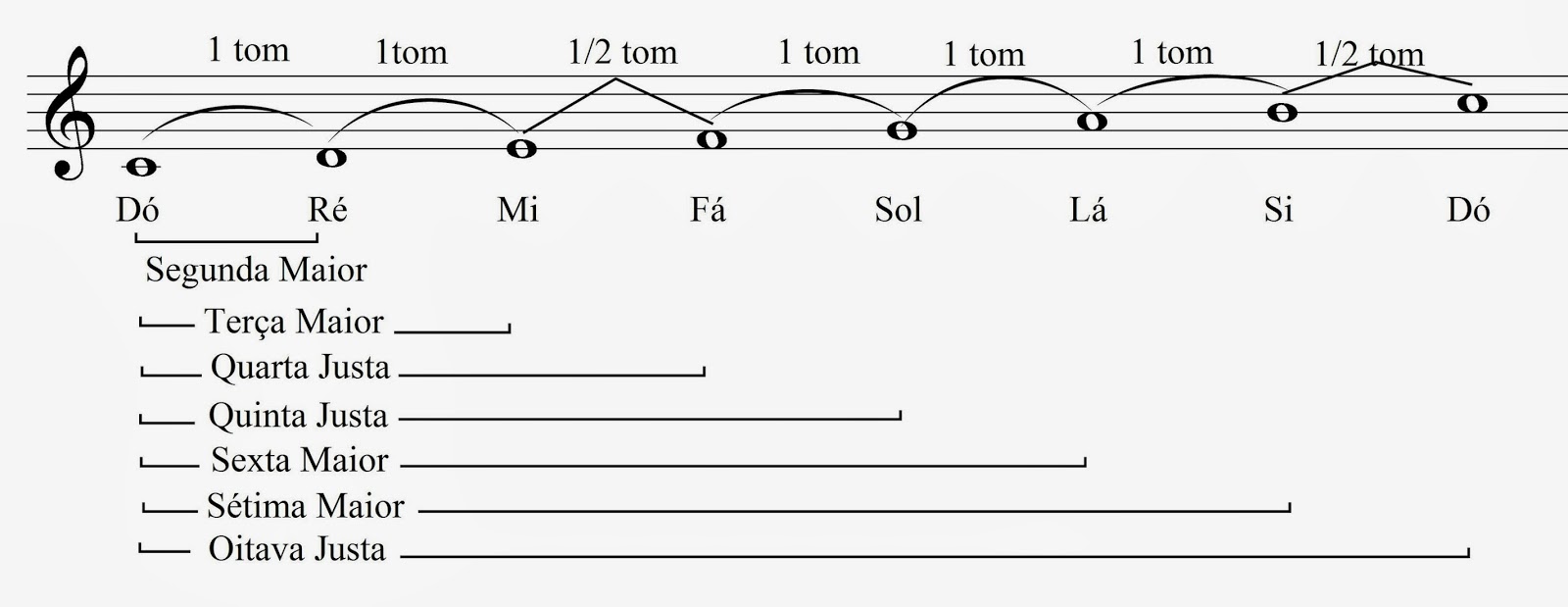
Assim, as frações [tex]\dfrac{1}{2}, \dfrac{3}{4}, \dfrac{2}{3}[/tex] correspondiam à oitava, à quarta e à quinta do som fundamental. Para um melhor entendimento dessas descobertas, vocês podem obter uma breve explicação sobre o significado das oitavas, quartas e quintas clicando no botão abaixo.

Escalas musicais são sequências ordenadas de notas. A escala mais conhecida é:
dó, ré, mi, fá, sol, lá, si, dó. . .
repetindo o ciclo de sete notas.
Já observamos que uma das características de uma nota é a sua altura e, contrariando a nossa intuição, as diferenças de altura entre notas consecutivas de uma escala não são as mesmas. Assim, tem sentido falarmos da menor diferença entre alturas de notas consecutivas de uma escala: na música ocidental, essa menor diferença é chamada de semitom e a diferença definida por dois semitons é chamada de tom. Uma escala musical costuma ser composta por 12 semitons.
A diferença entre as alturas de duas notas pode ser também chamada de distância ou intervalo entre as notas. Nos dias de hoje, os intervalos podem ser classificados como diminutos, menores, maiores, aumentados e justos. Na próxima figura, vemos alguns dos intervalos da escala dó, ré, mi, fá, sol, lá, si, dó, incluindo os três intervalos estudados por Pitágoras – a quarta justa, a quinta justa e a oitava justa.

Pitágoras verificou, também, que os sons produzidos tocando outras marcas de seu monocórdio resultavam dissonâncias, ou seja, sons não tão agradáveis como os anteriores. Então, Pitágoras descobriu que todos os intervalos musicais que ele considerava agradáveis eram apenas os regidos por estas três simples frações: [tex]\dfrac{1}{2}, \, \dfrac{3}{4}, \, \dfrac{2}{3}[/tex].
Segundo o pitagorismo, o número é o princípio essencial de que são compostas todas as coisas; assim, para eles, os números eram o verdadeiro elemento constituinte do mundo. Referiam-se ao “um” como o ponto, ao “dois” como a linha, ao “três” como a superfície e ao “quatro” como o sólido, de acordo com o número mínimo de pontos necessários para definir cada qual dessas dimensões. Com os pontos formavam as linhas; com as linhas formavam as superfícies e com estas formavam os volumes, portanto, a partir dos números [tex]1, 2, 3, 4[/tex], afirmavam que era possível construir o mundo. Como [tex]1 + 2 + 3 + 4 = 10[/tex], o número “dez” era visto pelos pitagóricos como um número perfeito, pois continha toda a harmonia da natureza e do cosmo. Não é à toa que a disposição geométrica desses quatro primeiros algarismos em forma triangular, denominada tetractys, representava para os pitagóricos a harmonia da natureza e do cosmo, ou seja, o “alicerce” das coisas do mundo. Assim, as relações musicais que, segundo os pitagóricos, determinavam as proporções relativas aos sons mais consonantes também estavam de acordo com o tetractys e portanto eram perfeitas!

Hoje, dispomos de outros conceitos e ferramentas modernas para entendermos esses fenômenos estudados por Pitágoras: podemos explicá-los por meio da frequência dos sons, conforme elucida de forma simples e divertida o vídeo a seguir. É só clicar na setinha.

Para passar a limpo e aprofundar o que foi aqui apresentado, assistam aos próximos vídeos e tentem responder as perguntas que aparecem após as respectivas telinhas.

Universidade Virtual do Estado de São Paulo – Matemática e Música: Parte 1

Universidade Virtual do Estado de São Paulo – Matemática e Música: Parte 2

Para assistir a uma animação do envolvimento dos pitagóricos com a música, clique na setinha.

Equipe COM – OBMEP