Clique no botão abaixo para visualizar a Sala.
Números Mórficos – Beleza e Clareza
|
Você quer desbravar o maravilhoso mundo dos números mórficos, onde todas as coisas têm a estética perfeita? Que bom, pois você está no lugar certo! |
 |
 |
Por que esse assunto é tão interessante? Para começar, esses números possuem uma propriedade chamada de ubiquidade, que é a habilidade de serem encontrados nos mais diversos lugares. Isto é, eles se fazem presentes na Aritmética, na Geometria, na Arte e até no nosso próprio corpo! |
Hora dos estudos
Comecemos com uma pequena definição:
Definição: Dizemos que um número real [tex]p\gt 1[/tex] é um número mórfico quando existem números naturais [tex]m~[/tex] e [tex]~n[/tex] tais que [tex]\boxed{p+1=p^m}~[/tex] e [tex]~\boxed{p-1=p^{-n}}.[/tex]
Vamos ver alguns exemplos:
Ele é a raiz positiva da equação [tex]p^2-p-1=0[/tex], que ao ser resolvida nos dá
[tex]\qquad p=\dfrac{1\pm\sqrt{\left(-1\right)^2-4\cdot 1 \cdot (-1)~}}{2}=\dfrac{1\pm\sqrt{5}}{2}.[/tex]
Tomando a raiz positiva temos que:
[tex]\varphi=\dfrac{1+\sqrt{5}}{2}\approx 1,618.[/tex]
Observe que como [tex]~\varphi^2-\varphi-1=0[/tex], então [tex]~\varphi^2-\varphi=1.[/tex]
Com isso, como [tex]\varphi\ne 0[/tex], [tex]\varphi-1=\dfrac{1}{\varphi}[/tex]; portanto, de fato, [tex]~\fcolorbox{black}{#d3cbc0}{$ \varphi+1=\varphi^2$}\,[/tex] e [tex]~\fcolorbox{black}{#d3cbc0}{$ \varphi-1=\varphi^{-1}$}\,.[/tex]
[tex] \psi = \sqrt[3]{\dfrac{9+\sqrt{69}}{18}} + \sqrt[3]{\dfrac{9-\sqrt{69}}{18}} \approx 1,3247.[/tex]
Para este caso, as justificativas de que [tex] \sqrt[3]{\dfrac{9+\sqrt{69}}{18}} + \sqrt[3]{\dfrac{9-\sqrt{69}}{18}}[/tex] é raiz da equação [tex]p^3-p-1=0[/tex] e de que [tex] \psi -1=\psi ^{-4}[/tex] são um pouquinho mais complicadas. Mas que tal você tentar?
Você pode conferir as duas justificativas clicando no próximo botão!
Veja uma aplicação magnífica do produto notável
[tex]\qquad (u+v)^3=u^3+3u^2v+3uv^2+v^3[/tex]
que pode ser rearranjado na forma
[tex]\qquad (u+v)^3-3uv(u+v)-(u^3+v^3)=0.[/tex]
Observe que se trata de uma identidade válida para qualquer escolha de números reais [tex]u~[/tex] e [tex]~v.[/tex] Assim, se pudermos escolher [tex]u~[/tex] e [tex]~v[/tex] de forma que [tex]3uv=1[/tex] e [tex]u^3+v^3=1[/tex], teremos então
[tex]\qquad (u+v)^3-(u+v)-1=0[/tex]
e a soma [tex]u+v[/tex] dos valores da nossa escolha para [tex]u~[/tex] e [tex]~v[/tex] será uma solução de [tex]p^3-p-1=0.[/tex]
Vamos, então, resolver o sistema
[tex] \qquad \begin{cases}3uv=1\\
u^3+v^3=1\end{cases}.[/tex]
Isolando [tex]v[/tex] na primeira equação e substituindo na segunda, temos que:
[tex] \qquad u^3+\dfrac{1}{27u^3}=1.[/tex]
Multiplicando ambos os lados dessa última equação por [tex] 27u^3[/tex], obtemos
[tex] \qquad 27\left(u^3\right)^2-27u^3+1=0.[/tex]
Fazendo a mudança da incógnita [tex]x=u^3[/tex], obtemos a equação do segundo grau [tex]27x^2-27x+1=0.[/tex]
Essa equação do segundo grau apresenta as raízes
[tex] \qquad x=\dfrac{9\pm\sqrt{69}}{18}.[/tex]
Escolhendo o valor [tex]x=\dfrac{9+\sqrt{69}}{18}[/tex] e lembrando que [tex] x=u^3[/tex], segue que:
[tex] \qquad u=\sqrt[3]{\dfrac{9+\sqrt{69}}{18}}.[/tex]
Substituindo esse valor para [tex]u[/tex] na equação [tex]u^3+v^3=1[/tex] obtemos
[tex] \qquad v=\sqrt[3]{\dfrac{9-\sqrt{69}}{18}}.[/tex]
Finalmente,
[tex] \qquad u+v=\sqrt[3]{\dfrac{9+\sqrt{69}}{18}}+\sqrt[3]{\dfrac{9-\sqrt{69}}{18}}.[/tex]
Observe que [tex]\sqrt[3]{\dfrac{9+\sqrt{69}}{18}}+\sqrt[3]{\dfrac{9-\sqrt{69}}{18}}[/tex] é um número real; as duas outras raízes da equação [tex]p^3-p-1=0[/tex] são números complexos e, particularmente, não interessam para a nossa discussão.
Observamos que existe uma fórmula de resolução de equações do 3º grau desse tipo: a fórmula de Tartaglia-Cardano. Se você tem interesse no assunto, visite esse site: Equações de Terceiro e Quarto Graus.
[tex]\quad \begin{align*} \left(p^3-p-1\right)\cdot\left(p^2-p+1\right)&=p^5-p^4+p^3-p^3+p^2-p-p^2+p-1\\
&=p^5-p^4-1.\end{align*}[/tex]
Assim, particularmente
[tex]\qquad \left(\psi^3-\psi-1\right)\cdot\left(\psi ^2-\psi+1\right)=\psi^5-\psi^4-1[/tex];
e, como [tex]\psi^3-\psi-1=0[/tex], então [tex] \psi^5-\psi^4-1=0[/tex], donde [tex] \psi^5-\psi^4=1.[/tex]
Como [tex]\psi \ne 0[/tex], podemos concluir que:
[tex]\qquad \dfrac{\psi^5-\psi^4}{\psi^4}=\dfrac{1}{\psi^4}\\
\qquad \psi-1=\psi^{-4}.[/tex]
De toda forma, [tex]~\fcolorbox{black}{#d3cbc0}{$ \psi+1=\psi^3$}\,[/tex] e [tex]~\fcolorbox{black}{#d3cbc0}{$ \psi-1=\psi^{-4}$}\,.[/tex]
 |
Você provavelmente espera que existam vários números mórficos, né? |
|
Agora, se arrume na cadeira e tome um bom gole do seu café (ou da sua água, se preferir), pois vamos falar mais especificamente sobre cada um destes números incrivelmente bonitos, e vamos precisar de toda a sua concentração! |

|
Número de Ouro ([tex]\varphi [/tex])
O Número de Ouro, também conhecido como razão áurea, traz consigo a ideia de beleza e harmonia desde a antiguidade. A letra [tex]\varphi[/tex] é utilizada em homenagem ao escultor grego Phidias, que viveu no século V a. C., pois acredita-se que ele utilizou este elegante número para construir suas obras de arte, como o monumento do Partenon e a estátua de Zeus.
|
|
|
Sem muita enrolação, vamos falar sobre propriedades do Número de Ouro,
que é a parte mais legal da conversa!
É bom deixar claro que esse número adora expressões infinitas!
Um exemplo disso é que ele pode ser encontrado em uma expressão de infinitas raízes quadradas! Não é incrível?
[tex] \varphi = \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}.[/tex]
Mas calma, que não para por aí. A razão áurea pode ser encontrada em infinitas frações contínuas também! Veja só:
[tex] \varphi = 1 +\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\cdots}}}}.[/tex]
[tex] \qquad a_1=\sqrt{1}=1;\quad a_2 = \sqrt{1+\sqrt{1}}\approx1,414;\quad a_3 =\sqrt{1+\sqrt{1+\sqrt{1}}}\approx 1,554;\\
\qquad a_4 =\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1}}}}\approx 1,598;\quad a_5 =\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1}}}}}\approx 1,612;[/tex]
e, de modo geral,
[tex]\qquad a_n=\sqrt{1+\sqrt{1+\cdots +\sqrt{1}}}[/tex], com [tex]n[/tex] raízes.
À medida que o valor de [tex]n[/tex] cresce, o valor de [tex]a_n[/tex] se aproxima cada vez mais de [tex]\varphi. [/tex] Simbolizamos isso usando a expressão com infinitas raízes quadradas.
Dessa forma, intuitivamente, se [tex]a=\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}[/tex], então [tex]a \gt 0[/tex] e
[tex]\quad a^2= 1 + \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}\\
\quad a^2= 1+a\\
\quad a^2-a-1=0.[/tex]
Com isso, temos que [tex]a[/tex] é a solução positiva da equação [tex]p^2-p-1=0[/tex], que sabemos ser [tex]\varphi.[/tex] Assim, [tex]a=\varphi[/tex], ou seja
[tex]\quad \boxed{~\varphi=\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}~}.[/tex]
Rigorosamente, para completar a justificativa da igualdade obtida, teríamos que garantir que a sequência
[tex]\qquad \left(1,~\,\sqrt{1+\sqrt{1}},\,\sqrt{1+\sqrt{1+\sqrt{1}}},\, \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1}}}},\, \cdots\right) [/tex]
é o que definimos matematicamente como uma “sequência convergente”. Mas isso foge completamente do objetivo desta Sala, que é uma Sala para Leitura!
Como você interpretaria a segunda igualdade?
|
Ainda não te convenci do quão legal que esse [tex]\varphi[/tex] é? Ora, vamos pensar um pouco. Tanto nas raízes quanto nas frações, a lógica de construção continua infinitamente. Sendo assim, a maioria das pessoas poderia achar que esses valores tenderiam para algo totalmente diferente. Todavia, elas convergem para um único número: o Número de Ouro. |
 |
Você sabia que o brilhante Euclides de Alexandria já tinha conhecimento da existência do Número de Ouro? Isso é verdade, pois, na sua majestosa obra “Os Elementos”, ele definiu geometricamente como encontrá-lo [1]. Assim, seguimos…
Definição: Diz-se que um segmento está dividido em média e extrema razão quando o todo está para a parte maior, assim como a parte maior está para a menor.
Observe a figura abaixo, na qual consideramos que os comprimentos dos segmentos [tex]\overline{AB}[/tex] e [tex]\overline{BC}[/tex] são [tex]a~[/tex] e [tex]~b[/tex], respectivamente.

Se [tex]\overline{AC}[/tex] estiver dividido em média e extrema razão, então segue que:
[tex]\qquad \dfrac{a+b}{a} = \dfrac{a}{b} \\
\qquad a^2 = ab+ b^2. \\
[/tex]
Dividindo ambos os lados da equação obtida por [tex]b^2[/tex], obtemos:
[tex]\qquad \dfrac{a^2}{b^2}=\dfrac{ab+ b^2}{b^2}\\
\qquad \left( \dfrac{a}{b} \right)^2 = \dfrac{a}{b}+1. \\
[/tex]
Vamos analisar a razão [tex]\dfrac{a}{b}.[/tex]
Fazendo [tex]\dfrac{a}{b}=p[/tex], teremos:
[tex]\qquad \left( p\right)^2 = p+1\\
\qquad \boxed{p^2-p-1=0}.\\
[/tex]
Assim, como [tex]\dfrac{a}{b}\gt 0[/tex], nos interessa a raiz positiva dessa equação, que sabemos ser [tex]\varphi .[/tex]
 |
Portanto, o valor da razão de [tex]a[/tex] por [tex]b[/tex] será o Número de Ouro! Concorda que esse número é uma perfeição? Além dessa, temos outra construção geométrica ainda baseada nele. Garanto que ela é igualmente interessante; mas é melhor deixar você tirar suas próprias conclusões! |
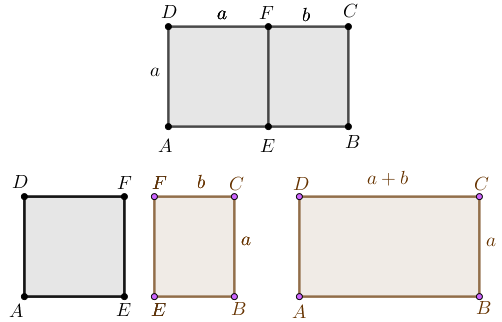
Definição: Chama-se retângulo áureo qualquer retângulo que, se dele suprimirmos um quadrado cujo lado é o menor dos lados do retângulo, o retângulo restante será semelhante ao retângulo original. Mais precisamente, o retângulo áureo é qualquer retângulo cuja razão do maior lado pelo menor resulta na razão áurea.
Para o retângulo [tex]ABCD[/tex] da figura abaixo, essa definição se traduz como: [tex]\dfrac{a+b}{a}=\dfrac{a}{b}=\varphi.[/tex]
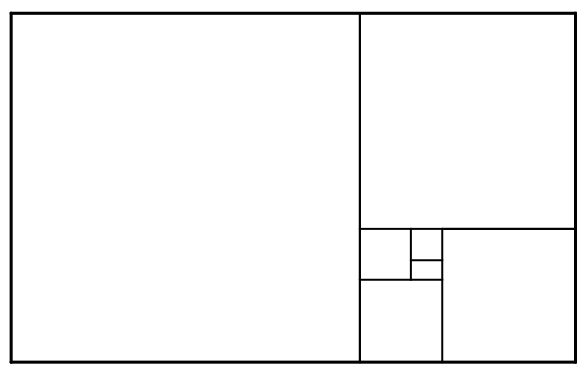
Uma consequência impressionante é o que acontece quando:
● a partir de um retângulo áureo eliminarmos um quadrado obtendo um segundo retângulo áureo interior ao original;
● a partir desse segundo retângulo áureo eliminarmos um quadrado obtendo um terceiro retângulo áureo interior ao segundo;
● a partir desse terceiro retângulo áureo eliminarmos um quadrado obtendo um quarto retângulo áureo interior ao terceiro;
● e assim sucessivamente…
Esse processo converge para um ponto específico, como mostrado na imagem abaixo.
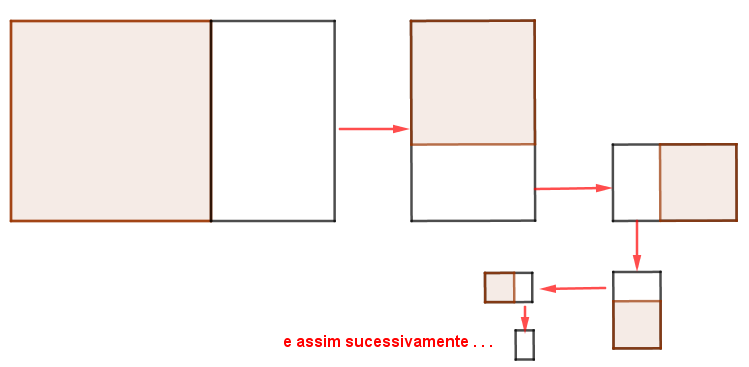
Na imagem a seguir, você consegue visualizar isoladamente os primeiros passos do processo descrito acima.
Ademais, outra consequência desse processo é que se tomarmos os arcos de um quarto de volta inscritos em cada quadrado, eles formarão uma curva que converge justamente para o ponto supracitado.
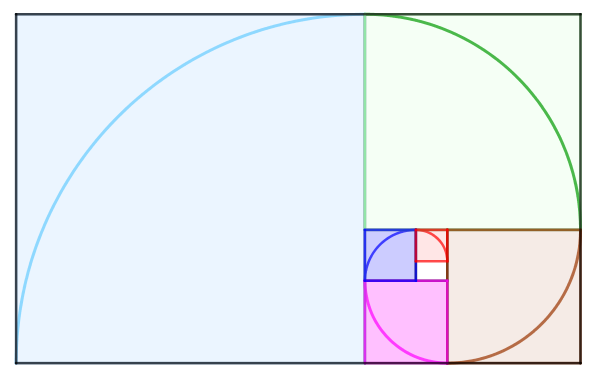
A essa curva damos o nome de “Espiral Áurea”. Observe-a destacada na imagem abaixo:
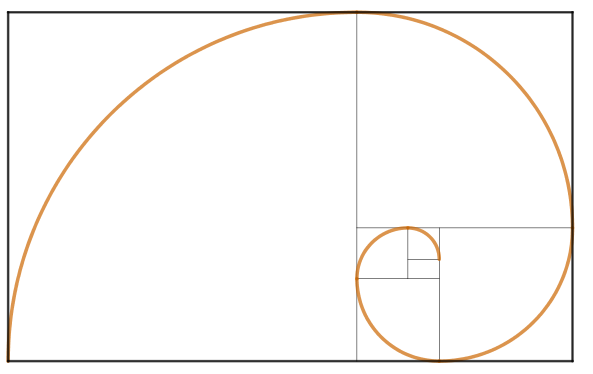
 |
É incrivelmente bonito, não é mesmo? Agora, vou lhe apresentar uma sequência mirabolante muito famosa, que foi muito utilizada por um italiano com ideias geniais. Acho que você vai gostar dela tanto quanto eu! |
Leonardo Fibonacci foi um grande matemático nascido na cidade de Pisa, na Itália, em 1170, aproximadamente. O problema da reprodução de coelhos, segundo [1], foi a força motriz da criação da famosa sequência, definida a seguir.
Definição: Chama-se Sequência de Fibonacci a sequência numérica definida por:
[tex]\qquad \qquad f_1 = f_2 = 1\\
\qquad \qquad f_n = f_{n-1} + f_{n-2}, \forall n\geq 3.[/tex]
Assim, a partir do terceiro, cada termo dessa sequência é a soma dos dois termos imediatamente anteriores e, portanto, a Sequência de Fibonacci terá a forma
[tex] \left(1,\, 1,\, 2,\, 3,\, 5,\, 8,\, 13,\, 21,\, 34,\, 55, \dots\right).[/tex]
 |
É melhor eu te avisar: se prepare! Pois agora vamos ver um teorema que definitivamente é muito bacana, mas que pode ser um pouquinho assustador! |
Considerando as soluções reais da equação [tex]p^2-p-1 = 0[/tex], se denotarmos por [tex]\varphi[/tex] a solução positiva e [tex]\phi[/tex] a solução negativa, teremos:
[tex] f_n = \dfrac{1}{\sqrt5} \cdot \left[ \varphi^n -\phi^n \right].[/tex]

|
Observe que os números da sequência de Fibonacci são todos inteiros, mas, na equação acima, temos vários números irracionais. Essa é a mágica dessa fórmula! A partir disso, vou deixar uma pequena atividade para você: faça o teste, coloque [tex]n = 2~[/tex] e [tex]~n=3[/tex] e veja se os resultados batem com o 2º e o 3º termos da sequência, respectivamente. |
Vamos fazer um pequeno experimento? Tendo uma calculadora em mãos, escolha um número qualquer (que não seja o primeiro) da Sequência de Fibonacci, que nós já conhecemos, e divida-o pelo seu antecessor. Faça isso novamente, escolhendo um outro número da sequência que seja maior que o escolhido inicialmente e dividindo-o pelo seu antecessor. Faça isso mais algumas vezes. Para te ajudar, aqui estão alguns números da sequência:
[tex]\qquad \qquad 1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55,\ 89,\ 144,\ 233,\ 377,\ 610,\ 987,\ 1597,\ 2584,\ 4181, \dots.[/tex]
 |
E aí? Reparou em algum detalhe muito, muito, MUITO legal enquanto fazia o experimento? |
[tex] \displaystyle \lim_{n\rightarrow \infty} \dfrac{f_{n+1}}{f_n} = \varphi.[/tex]
Veja o quão grande é a magnificência desse teorema! Se você nunca ouviu falar em limites (representado por “[tex]\lim[/tex]” na equação acima), não tem problema, pois é mais simples do que parece. Sua função nesta equação é, basicamente, tomar valores de [tex]n[/tex] tendendo ao infinito, ou seja, valores de [tex]n[/tex] tão grandes quanto se queira, e cada vez maiores!. Nesse caso, quanto maior o índice escolhido da sequência de Fibonacci, ao dividir o respectivo termo da sequência pelo seu antecessor, esse quociente dará mais próximo do valor da razão áurea.

|
Por fim, há uma propriedade algébrica que envolve as potências do Número de Ouro e a Sequência de Fibonacci. Tem como ser melhor que isso? Fica ligado! |
[tex]\varphi^2 = \varphi + 1\\ \varphi^3 = 2\varphi + 1\\ \varphi^4 = 3\varphi + 2\\ \varphi ^5 = 5\varphi + 3 \\ \varphi^6 = 8\varphi +5 \\ \qquad \vdots \\ \boxed{\varphi^n = f_n\cdot \varphi + f_{n-1}}.[/tex]
[tex]\varphi^3=\varphi^2\cdot \varphi= (1+\varphi)\cdot \varphi=\varphi+\varphi^2=\varphi+(1+\varphi)=1+2\varphi[/tex]
[tex]\varphi^4=\varphi^3\cdot \varphi= (1+2\varphi)\cdot \varphi=\varphi+2\varphi^2=\varphi+2(1+\varphi)=2+3\varphi[/tex]
[tex]\varphi^5=\varphi^4\cdot \varphi= (2+3\varphi)\cdot \varphi=2\varphi+3\varphi^2=2\varphi+3(1+\varphi)=3+5\varphi\\
\vdots [/tex]

|
A íntima relação entre a razão áurea e a sequência de Fibonacci faz essa última propriedade ser ainda mais especial! Por sinal, ela envolve conceitos tão bonitos e harmoniosos que seria um desperdício não usá-la em questões. Tanto é que ela já apareceu no ENEM (Exame Nacional do Ensino Médio). Vamos conferir? |
Assim como a potência [tex]\varphi^2[/tex], as potências superiores de [tex]\varphi[/tex] podem ser expressas da forma [tex]a\cdot \varphi+b[/tex], em que [tex]a~[/tex] e [tex]~b[/tex] são inteiros positivos, como apresentado no quadro.

A potência [tex]\varphi^7[/tex] , escrita na forma [tex]a\cdot \varphi + b[/tex] ([tex]a~[/tex] e [tex]~b[/tex] são inteiros positivos), é:
a) [tex]5\varphi + 3[/tex]
b) [tex]7\varphi + 2[/tex]
c) [tex]9\varphi + 6[/tex]
d) [tex]11\varphi + 7[/tex]
e) [tex]13\varphi + 8[/tex]
[tex]\qquad \varphi^7=\varphi \times \varphi^6=\varphi \times(8\varphi + 5).[/tex]
Aplicando a propriedade distributiva, temos:
[tex]\qquad \varphi^7=8\varphi^2 +5 \varphi.[/tex]
Como [tex]\varphi^2=\varphi+1[/tex], então segue que:
[tex]\qquad \varphi^7=8 \times (\varphi +1) +5 \varphi \\
\qquad \boxed{\varphi^7= 13\varphi +8}.[/tex]
Portanto, a resposta é a alternativa e).
 |
Eu sei que você está mais instigado do que nunca a estudar sobre a razão áurea, mas nosso objetivo é apenas te introduzir nesse mundo mágico! Se quiser saber mais sobre ela, dá uma olhadinha nesta sala de atividades: A Razão Áurea. |
Número Plástico ([tex]\psi[/tex])

|
Agora, vamos olhar com mais ternura para este outro número mórfico. Já imaginou se existisse um número que funcionasse igual ao número de ouro, mas em três dimensões? Acho que você já está entendendo aonde eu quero chegar. Esse número existe, como veremos a seguir! |
O monge e arquiteto holandês Hans van der Laan (1904-1991) havia criado algo que ninguém da sua época esperava: um novo sistema de medidas baseado em um número irracional, denominado por ele de “número plástico”. Ele explicou que esse número é uma resposta tridimensional da razão áurea e que, diferentemente dela, ele estaria menos ligado à beleza e mais ligado ao que ele chamou de “clareza de percepção” [1], [4], [9]. Como vimos anteriormente, o número plástico é definido como a única solução real da equação [tex]p^3 = p +1[/tex] e é aproximadamente [tex]1,3247.[/tex]
 |
Como se trata de um assunto relativamente novo, ainda não há muito material disponível a respeito do número plástico (já fica a dica para os futuros estudiosos da área). Mas vamos ver algumas propriedades que esse número tem. Eu aposto que você vai se surpreender! |
O número plástico pode ser determinado por uma expressão de infinitas raízes cúbicas. Você já viu algo parecido em algum lugar né? Saca só:
[tex] \psi = \sqrt[3]{1+\sqrt[3]{1+\sqrt[3]{1+\sqrt[3]{1+\cdots}}}}.[/tex]
Além disso, assim como é possível dividir um segmento obedecendo a “razão áurea”, também é possível fazer isso com a “razão plástica”. Vejamos sua definição:
Definição: Um segmento [tex]\overline{AB}[/tex] é divido em três partes pelos pontos [tex]C~[/tex] e [tex]~D[/tex] na razão plástica quando:
[tex]\qquad \qquad \dfrac{AB}{AD} = \dfrac{AD}{BC} = \dfrac{BC}{AC} = \dfrac{AC}{CD} = \dfrac{CD}{BD}.[/tex]
Quando isso acontece, um segmento [tex]\overline{AB}[/tex] qualquer fica semelhante ao que aparece na próxima imagem.
![]()
|
Utilizando a mesma lógica algébrica da razão áurea, perceberemos que as razões que aparecem na definição acima são iguais a [tex]\psi[/tex]. Mas, como diria o astuto matemático francês Pierre de Fermat: |
 |
Você já deve ter percebido que os números mórficos têm muito em comum um com o outro. Sendo assim, vejamos mais um conceito parecido entre ambos!
A razão áurea possui um retângulo áureo, e isso você já sabe. Então, adivinha?
O número plástico também possui uma figura plástica! Mas aqui, não é um retângulo, e sim um pentágono, chamado de “pentágono plástico”.
Definição: O pentágono plástico é um pentágono que possui um ângulo interno medindo [tex]60^\circ[/tex] e os demais medindo [tex]120^\circ[/tex]; além disso, os seus lados formam uma progressão geométrica crescente de razão [tex]\psi.[/tex]
Observe na imagem abaixo que esse pentágono é gerado ao tomarmos um paralelogramo de lados [tex]1+\psi,\, \psi^2+\psi,\, \psi^3~[/tex] e [tex]~\psi^4[/tex] e suprimirmos dele um triângulo equilátero de lados medindo [tex]\psi[/tex] dos lados [tex]1+\psi[/tex] e [tex] \psi^2+\psi[/tex], como ilustra a imagem a seguir.

O que é majestoso aqui é que, assim como o retângulo áureo, o pentágono plástico possui a característica de auto propagação. Para observarmos isso, basta suprimirmos triângulos equiláteros de pentágonos plásticos em infinitas etapas, gerando em cada etapa pentágonos plásticos semelhantes.
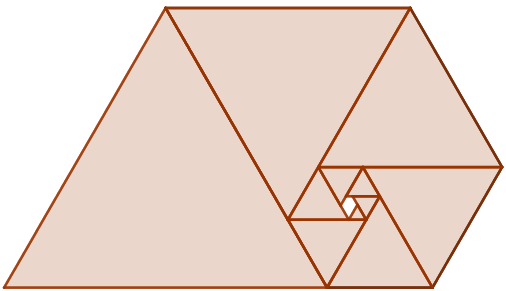
Na imagem a seguir, você consegue visualizar isoladamente os primeiros passos do processo.

E, assim como a espiral áurea, a partir de uma sequência de pentágonos plásticos, podemos traçar arcos circunscritos de 1/6 de volta com centro no vértice de cada triângulo suprimido e que intercepta os outros dois vértices para obter uma curva que foi definida como “espiral plástica” em [1].
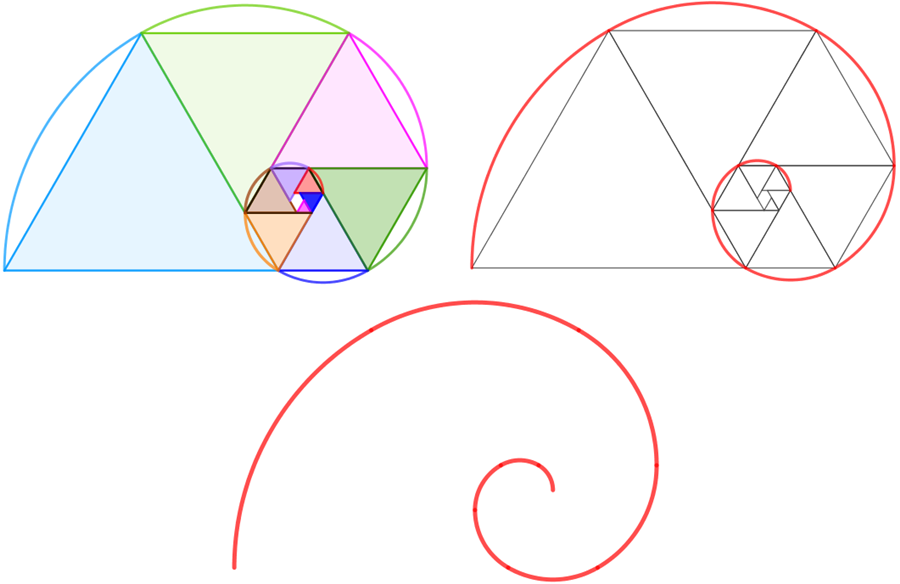
Sequência de Padovan
 |
Essa é uma sequência nova e muito específica; recebeu esse nome em homenagem à Richard Padovan, que ajudou a descrevê-la, há não muito tempo atrás. É interessante pensar dessa forma; pois, normalmente, os assuntos que estudamos foram propostos vários séculos atrás. |
O britânico Richard Padovan, nascido em 1935, estudou arquitetura em Londres e, desde que se deparou com os trabalhos de Hans van der Laan, citado anteriormente, tem dedicado sua vida ao estudo, prática e ensino da arquitetura. Tendo isso em mente, a sequência de Padovan é uma sucessão que segue uma lógica semelhante à da sequência de Fibonacci. Ela é definida da seguinte forma:
Definição: Chama-se sequência de Padovan a sequência definida por:
[tex]\qquad P_1 = P_2 = P_3 = 1\\
\qquad P_n = P_{n-2} + P_{n-3}, ~\forall n\geq 4 .[/tex]
Atribuindo valores para [tex]n[/tex], teremos:
[tex] \left(1,\ 1,\ 1,\ 2,\ 2,\ 3,\ 4,\ 5,\ 7,\ 9,\ 12,\ 16,\ 21,\ \dots\right).[/tex]

|
Fica esperto! Alguns autores escrevem a definição acima começando por [tex]P_0.[/tex] No entanto, para ficar similar à de Fibonacci, a qual já estamos muito bem familiarizados, decidimos começar também por [tex]P_1[/tex]. Portanto, seguimos agora com um teorema majestoso, para dizer o mínimo. |
[tex]\displaystyle \lim_{n\rightarrow \infty} \dfrac{P_{n+1}}{P_n} = \psi.[/tex]
Essa é outra semelhança cabal com o número de ouro! Lembra do conceito de limite utilizado anteriormente? Estamos utilizando-o novamente aqui. Espero que você fique tão feliz quanto eu em saber que, à medida que pegamos valores suficientemente grandes da sequência de Padovan e dividimos pelo seu antecessor, esses quocientes tendem a dar o valor do número plástico!
Seguem alguns números da sequência para que você, ao utilizar sua calculadora, perceba esse fato.
[tex]\qquad \qquad 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, 351, 465, 616,\dots [/tex]
Lembra do valor do número plástico?
Segue uma aproximação: [tex]\psi \approx 1,3247. [/tex]
Para um aprofundamento maior sobre o número plástico e a sequência de Padovan, utilizem as fontes [1], [2] e [5].
 |
Quer saber de uma curiosidade que vai te deixar de queixo caído? A melhor referência que conseguimos desse assunto é justamente de um professor brasileiro da Paraíba [1]. Isso serve para mostrar como a pesquisa matemática, no Brasil, também está a todo vapor! |
 |
Chegamos ao fim da nossa breve conversa, caro(a) leitor(a). Espero que você tenha gostado dessa pequena caminhada pelo mundo dos números mórficos! Estou na torcida para que você, em algum momento, possa utilizar desse conhecimento adquirido de forma produtiva e eficaz! |
Esperamos que você tenha se divertido!
Até a próxima…

Membros do COM Phidias.
COM Phidias (EEEFM Maestro José Siqueira – Conceição, PB)
Equipe COM – OBMEP
[1] FERREIRA, R. Números mórficos. João Pessoa: Imprell Gráfica e Editora, 2015. PROFMAT (Acesso em 23/11/2023).
[2] EUCLIDES. Os Elementos. São Paulo: Editora UNESP, 2009.
[3] Euclides de Alexandria: Clubes de Matemática da OBMEP. (Acesso em 23/11/2023).
[4] Plastic Number: Wikipédia (Acesso em 23/11/2023).
[5] Morphic Numbers (Acesso em 23/11/2023).
[6] O Partenon: InfoEscola (Acesso em 23/11/2023).
[7] Estátua de Zeus: Wikipédia(Acesso em 23/11/2023).
[8] Richard Padovan: Wikipédia (Acesso em 23/11/2023).
[9] Dom Hans van der Laan (Acesso em 23/11/2023).
[10] Atividade: A Razão Áurea. Clubes de Matemática da OBMEP (Acesso em 23/11/2023).
[11] INEP: Provas anteriores do ENEM. INEP (Acesso em 23/11/2023).

 Imagem extraída de
Imagem extraída de  Imagem extraída de
Imagem extraída de