Salve, explorador(a)!
Como foi o passeio pelo mundo da Equação Quadrática? Da Mesopotâmia às fórmulas de Viète, passando por Euclides, Bháskara, e chegando a alguns exercícios “bugantes”, com certeza sua mochila volta cheia de ferramentas incríveis. Agora é hora de usar essas ferramentas! Afinal,
“Tudo o que fazemos é baseado em alguma estrutura matemática e, embora a matemática seja muitas vezes considerada abstrata, é fundamental para como entendemos a natureza, o universo maior, com suas dimensões de tempo e espaço e uma infinidade de incertezas.” Fonte: Mathematics for Action, UNESCO, 2022.
Então, apresentamos a Sala
Voltando de um passeio pelo mundo da Equação Quadrática
Ideias e aplicações
Nesta sala, veremos como utilizar as equações quadráticas para diversos tipos de problemas: problemas de comprimentos e áreas, problemas de movimento, custo e receita, e questões envolvendo parábolas. Depois disso, apresentaremos algumas atividades preparadas especialmente para futuros astronautas. Vamos?!
Problemas de Comprimentos e Áreas
Quando pensamos em cálculos de áreas, pensamos em alguma coisa “ao quadrado”. Por exemplo, qual é a unidade de medida utilizada quando alguém vai comprar um imóvel? Em geral, o “metro quadrado”, ou seja, a área de um quadrado de lado 1 metro. Se tivermos o valor da área, por exemplo, de um quadrado cujo lado é desconhecido (digamos, de medida [tex]x[/tex]), podemos igualar a área conhecida a [tex]x^2[/tex] para encontrar a medida do lado.
Para aquecer, qual seria a área de:
- Uma circunferência de raio [tex]x[/tex]?
- Um triângulo equilátero de lado [tex]x[/tex]?
- Um retângulo cujo menor lado mede [tex]x[/tex] e o maior lado possui 1 unidade de comprimento a mais?
Pois é! Todas estas respostas envolvem um termo de grau dois, o famoso [tex]x^2[/tex]. De fato, a equação quadrática pode ser uma ferramenta importante na resolução de problemas envolvendo áreas. Vejamos um exemplo:
Questão 1
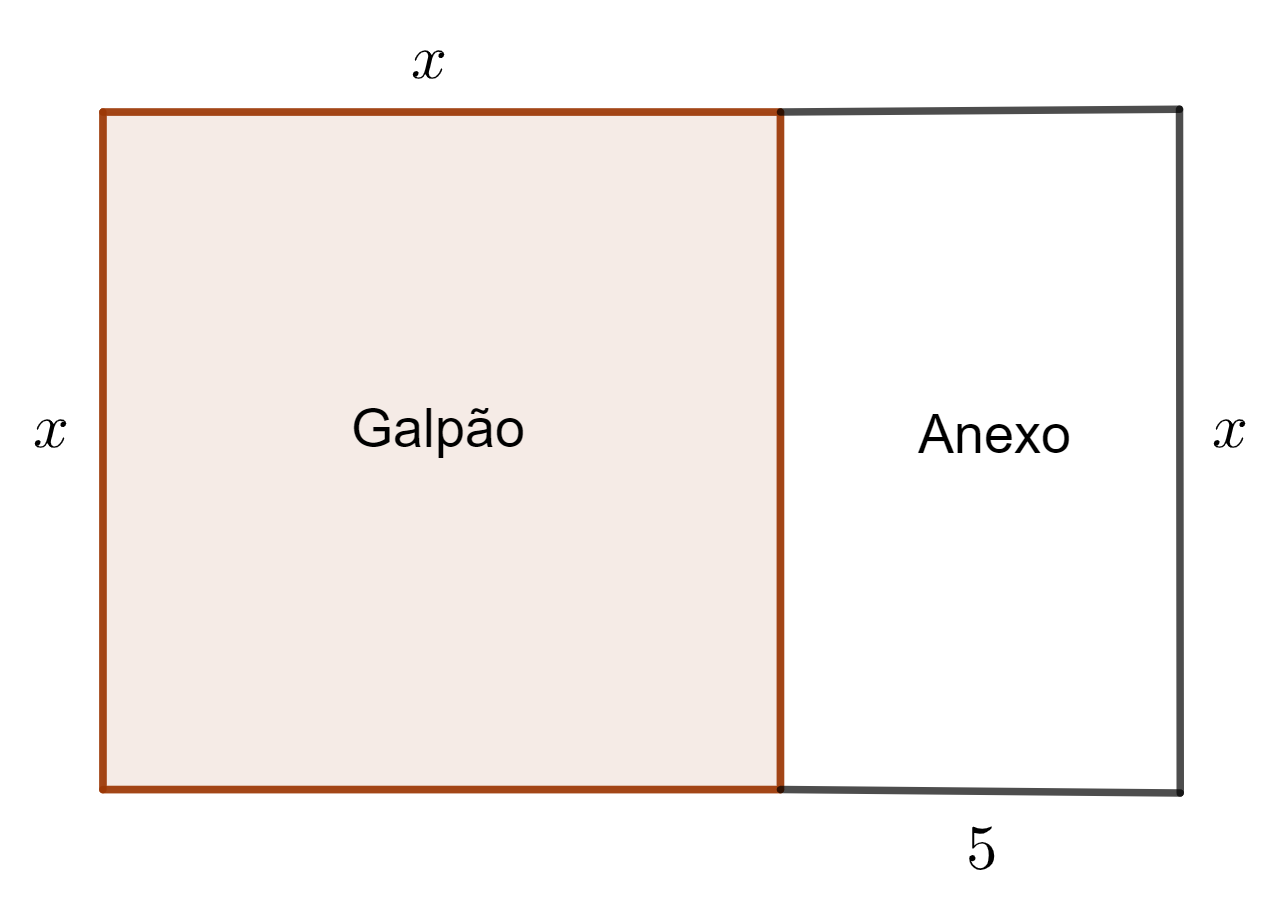
Em um dos lados de um galpão quadrado, foi construído um anexo de mesma largura, e comprimento de [tex]5[/tex] metros. A área total da construção é de [tex]100~\text{m}^2[/tex]. Qual é a área do galpão?
Outra aplicação muito importante das equações quadráticas pode surgir em questões que são resolvidas pelo Teorema de Pitágoras. Por exemplo: Qual triângulo retângulo tem os lados em uma progressão aritmética de razão 1? Relembrando, o Teorema de Pitágoras afirma que, em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos. Assim, o problema pode ser traduzido na forma [tex]x^2+(x+1)^2=(x+2)^2[/tex], o que pode ser reorganizado em uma equação quadrática. Ao resolvê-la, você encontrará um dos triângulos retângulos mais famosos de todos.
Vejamos um exemplo um pouco mais elaborado:
(Canguru, 2014 – Adaptado) O quadrado [tex]XYZW[/tex] tem os vértices [tex]X[/tex] e [tex]Y[/tex] sobre a reta [tex]r[/tex] e os vértices [tex]Z[/tex] e [tex]W[/tex] sobre as circunferências de centros [tex]O[/tex] e [tex]O′[/tex], sendo essas circunferências, de raios medindo [tex]2 \text{ cm}[/tex], tangentes entre si e à reta [tex]r[/tex], como na figura abaixo.
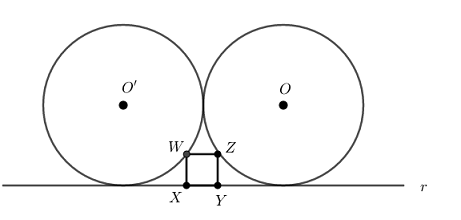
Encontre a medida do lado do quadrado [tex]XYZW[/tex].
Atividade em grupo 1
Propomos um trabalho de modelagem matemática que visa calcular áreas das superfícies de diversas caixas retangulares após terem todas as dimensões diminuídas igualmente. A atividade deve ser desenvolvida em pequenos grupos, ou duplas.
 Materiais necessários:
Materiais necessários:
- Folhas de papel para anotações;
- Uma régua por aluno;
- Caixas retangulares, diversas por grupo;
- Tesoura, uma por grupo.
Procedimentos (para cada caixa):
- Anotar em uma tabela as medidas dos lados da caixa e área superficial da mesma.
- Planificar a caixa e separar as faces.
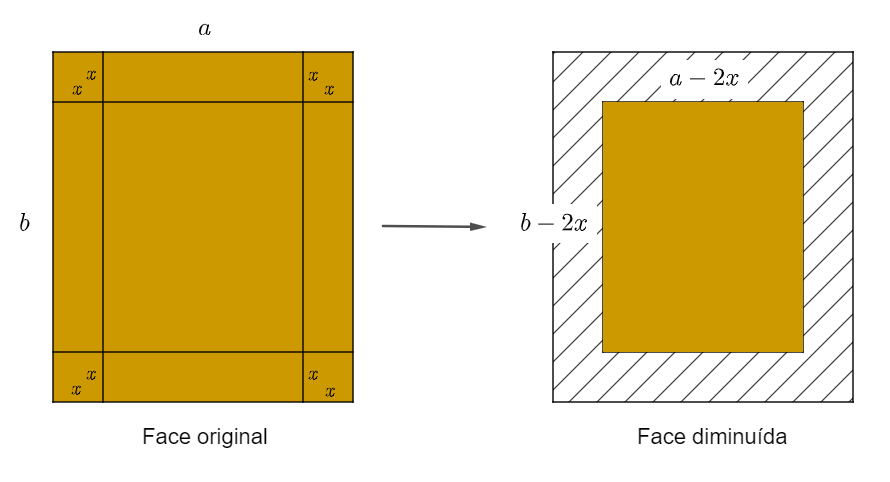
- Para diferentes medidas [tex]x[/tex] (menor que a metade do menor lado da caixa), diminuir todos os lados das faces como na figura e anotar a área superficial [tex]A(x)[/tex] total de uma caixa montada com as faces diminuídas:
- Encontrar uma equação para [tex]A(x)[/tex] que descreva a situação trabalhada dadas as dimensões iniciais da caixa [tex]a, b[/tex] e [tex]c[/tex], e a medida [tex]x[/tex]. Comparar os resultados obtidos experimentalmente com o modelo criado.
- Discutir os resultados: Qual é o valor de [tex]x[/tex] que faz com que a área superficial da caixa seja a metade da área original? Para este valor de [tex]x[/tex], como se comparam os volumes? A equação [tex]A(x)[/tex] pode ser a mesma para duas caixas de diferentes dimensões? O que deve ser igual em duas caixas para que [tex]A(x)[/tex] possua a mesma expressão?
Problemas de Movimento
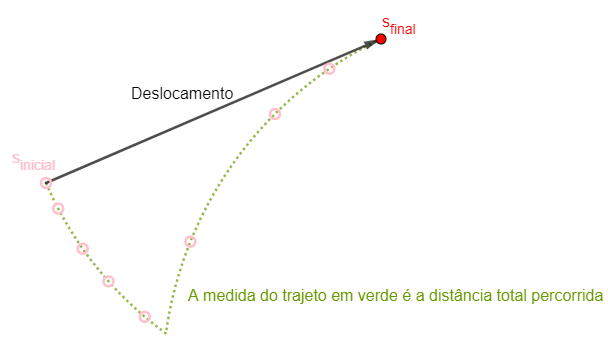
Quando um objeto está em movimento, ele muda de posição ao longo do percurso. Para descrevermos o movimento de um objeto, precisamos conhecer os conceitos de deslocamento, distância percorrida e velocidade.
[tex]d=\Delta s=s_{final}-s_{inicial}.[/tex]
O deslocamento é uma grandeza vetorial. Isso significa que ele tem uma direção, um sentido e uma magnitude (ou módulo), podendo ser representado visualmente como uma seta que aponta da posição inicial para a posição final. Quando você começa um problema de deslocamento, deve saber ou escolher a orientação positiva. Em deslocamentos horizontais, geralmente o sentido positivo é o da direita; em deslocamentos verticais, geralmente o sentido positivo é para cima. Mas, esta orientação pode ser diferente dependendo do problema.
Já a distância percorrida é o comprimento total do caminho percorrido entre duas posições: é uma grandeza escalar, não possuindo direção nem sentido.
A velocidade do objeto é, como o deslocamento, uma grandeza vetorial, possuindo direção, sentido e magnitude. Ela é definida levando-se em consideração o deslocamento do objeto em um determinado intervalo de tempo, ou seja, a velocidade diz respeito à mudança da posição com relação ao tempo.
Se conhecermos o deslocamento em certo intervalo de tempo, podemos dividir o deslocamento pelo tempo total de percurso, obtendo o que chamamos de velocidade vetorial média do objeto neste intervalo de tempo:
[tex]\boxed{\text{velocidade média}=\frac{\text{deslocamento}}{\text{tempo gasto}}}[/tex].
Ou seja,
[tex]\boxed{v_{media}=\frac{s_{final}-s_{inicial}}{\Delta t}}[/tex].
É importante dar atenção às unidades de medida. Se, por exemplo, a magnitude da velocidade é em quilômetros/hora, a magnitude do deslocamento é em quilômetros e o tempo é em horas.
Algumas vezes, porém, não estamos interessados na direção do deslocamento: queremos apenas saber quão rápido o objeto se move. Nestes casos, podemos considerar apenas a velocidade escalar, que é sempre positiva, não possuindo direção ou sentido, diz respeito à distância percorrida em um intervalo de tempo:
[tex]\boxed{\text{velocidade escalar média}=\frac{\text{distância percorrida}}{\text{tempo gasto}}}[/tex].
Tanto na velocidade vetorial quanto na velocidade escalar, quanto menor o intervalo de tempo considerado, mais detalhada é a informação. Em um intervalo “infinitamente pequeno” (o que, formalmente, requer o uso de limites e foge do escopo desta sala), a velocidade vetorial média se torna a velocidade vetorial instantânea. O velocímetro de um carro, por exemplo, mostra a magnitude (mas não a direção, nem o sentido) da velocidade vetorial instantânea do carro. A magnitude da velocidade vetorial instantânea é justamente a velocidade escalar instantânea do objeto.
Problemas envolvendo uma velocidade constante geralmente são resolvidos via equações polinomiais do 1° grau. O exemplo mais comum é o do movimento uniforme, que ocorre quando um objeto desloca-se em linha reta com velocidade constante. Considerando uma velocidade constante, a velocidade instantânea (vetorial ou escalar) é igual à velocidade média (vetorial ou escalar, respectivamente) em qualquer intervalo de tempo. Neste caso, a magnitude da velocidade vetorial é sempre igual à velocidade escalar.
Vejamos um exemplo: quanto tempo você leva para atravessar um campo de futebol de [tex]100~\text{m}[/tex] de comprimento, movendo-se em linha reta a uma velocidade constante de [tex]3~\text{km/h}[/tex]?
Como o comprimento do campo de futebol foi dado em metros, observe que sua velocidade tem magnitude 3000 m/h. Considerando a direção horizontal e o sentido no qual você corre como positivo, sua posição final é [tex]s_f=100[/tex], enquanto sua posição inicial é [tex]s_i=0.[/tex] O tempo total, em horas, será dado pela seguinte equação do primeiro grau:
[tex]\qquad s_f=s_i+v t[/tex]
[tex]\qquad 100=0+3000 t[/tex]
[tex]\qquad t=1/30.[/tex]
Assim, você gastará [tex]1/30[/tex] de uma hora, ou [tex]60/30=2[/tex] minutos para cruzar o campo.
Porém, muitas vezes estamos interessados em um movimento no qual a velocidade se modifica, ou seja, existe uma aceleração.
[tex]a_{media}=\dfrac{\Delta v}{\Delta t}=\dfrac{v_{final}-v_{inicial}}{\Delta t}.[/tex]
Para a aceleração vetorial instantânea, precisaríamos considerar um intervalo de tempo infinitamente pequeno, o que requer, mais uma vez, o uso de limites.
Já a aceleração escalar média é definida como a variação da velocidade escalar em função do tempo. Com um intervalo de tempo cada vez menor, obtemos, no limite, a aceleração escalar instantânea, que é justamente a magnitude da aceleração vetorial instantânea.
Nesta sala, consideramos apenas situações nas quais a aceleração é constante, de forma que a aceleração instantânea (vetorial ou escalar) é igual à aceleração média (vetorial ou escalar, respectivamente) em qualquer intervalo de tempo. Neste caso, a magnitude da aceleração vetorial é sempre igual à aceleração escalar.
Problemas envolvendo uma aceleração constante podem necessitar de uma equação quadrática para serem resolvidos. O exemplo mais comum é o do movimento uniformemente variado, que ocorre quando um objeto desloca-se em linha reta e com aceleração constante. Por exemplo, quando você lança um objeto para cima com uma velocidade (velocidade vetorial instantânea, cuja magnitude é a velocidade escalar instantânea) inicial [tex]v_0[/tex], a aceleração da gravidade (aceleração vetorial instantânea, cuja magnitude é a aceleração escalar instantânea) faz com que ele suba no ar cada vez mais devagar, para depois descer cada vez mais rápido. De maneira geral, a velocidade de um objeto em movimento uniformemente variado num tempo [tex]t[/tex] é dada por
[tex]v(t)=v_0+at,[/tex]
onde [tex]v_0[/tex] é a velocidade inicial e [tex]a[/tex] é a aceleração:
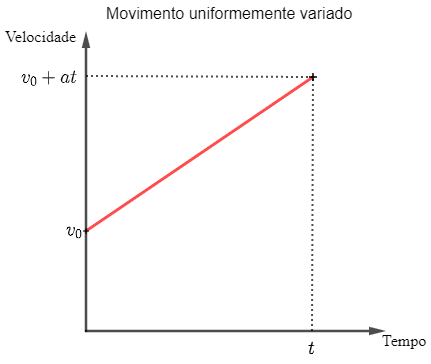
A magnitude do deslocamento do objeto, em cada instante, será informada por uma função quadrática em [tex]t[/tex]. Vejamos como. Para encontrar o deslocamento, utilizaremos a velocidade média do objeto em um espaço de tempo [tex]\Delta t=t-0=t[/tex]. Isso não é tão simples, porque, a priori, temos infinitas velocidades entre [tex]v_0[/tex] e [tex]v_0+at[/tex]. Para entender como encontramos a velocidade média, suponha que sabemos apenas a velocidade inicial e a velocidade final. Neste caso, nossa primeira aproximação para a velocidade média do objeto seria
[tex]v_{media}=\frac{v_0+v_0+at}{2}=v_0+a\frac{t}{2}.[/tex]
Agora, supomos que conhecemos também a velocidade em [tex]\frac{t}{2}[/tex]. De fato a conhecemos:
[tex]\qquad v\left(\frac{t}{2}\right)=v_0+a\frac{t}{2}.[/tex]
Como fica nossa aproximação neste caso? E se considerássemos, além do tempo [tex]\frac{t}{2}[/tex], os tempos [tex]\frac{t}{4}[/tex] e [tex]\frac{3t}{4}[/tex]? Observe na figura abaixo o cálculo das médias:
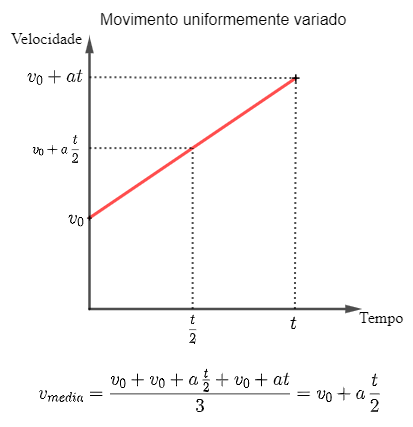
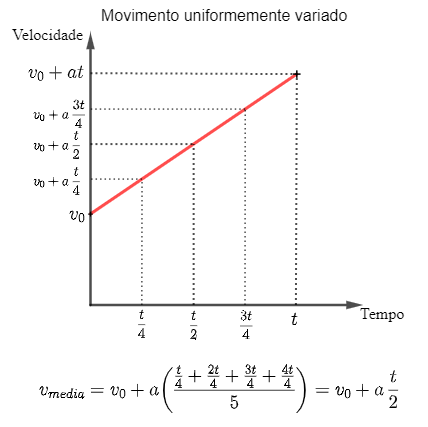
Uma justificativa formal foge do escopo desta sala, mas você pode perceber que, considerando mais e mais medições, nos aproximamos da velocidade média exata (aquela que seria definida por todas as infinitas medições), e esta é, justamente, [tex]v_{media}=v_0+a\frac{t}{2}.[/tex]
Portanto, o deslocamento do objeto em um tempo [tex]t[/tex] é dado por
[tex]\qquad d(t)=\left(v_0+a\dfrac{t}{2}\right)t=\frac{a}{2}t^2+v_0t.[/tex]
Como [tex]d(t)=s(t)-s_{inicial},[/tex] temos
[tex]\qquad s(t)-s_{inicial}=\frac{a}{2}t^2+v_0t,[/tex]
[tex]\qquad s(t)=\frac{a}{2}t^2+v_0t+s_{inicial},[/tex]
uma função quadrática!
Vejamos um exemplo de aplicação:
De uma altura de [tex]2\text{ m}[/tex] em relação ao solo, lança-se uma bola para cima com velocidade de [tex]10\text{ m/s}[/tex]. Daqui a quanto tempo ela atingirá o solo?
Encontrar a velocidade de um determinado objeto também pode levar à resolução de uma equação quadrática, e isso pode ser utilizado, por exemplo, por esportistas.
Um caiaque está subindo um rio que flui a [tex]2 \text{ km/h}[/tex]. Qual deve ser a velocidade aplicada do caiaque para que um percurso de [tex]15 \text{ km}[/tex] seja realizado em [tex]3 \text{ h}[/tex] (ida e volta)?
Custo, receita e otimização
As funções quadráticas podem modelar diversas situações de custo/benefício, além de possuírem uma fórmula simples para seu ponto máximo/mínimo e seu respectivo valor máximo/mínimo. Assim, são muito utilizadas em problemas de otimização, onde precisamos encontrar um valor ou tempo ótimo ou extremo em determinado contexto.
O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola do gráfico de [tex]h[/tex] são dadas por:
[tex]\qquad \qquad (x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex],
sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
- o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
- o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Particularmente, se [tex]\Delta \gt 0[/tex], [tex]x_v[/tex] é a média entre as duas raízes de [tex]h[/tex]: [tex]x_v=\dfrac{r_1+r_2}{2}.[/tex]
Visualizem as informações, se [tex]\Delta \gt 0[/tex], nos gráficos abaixo:
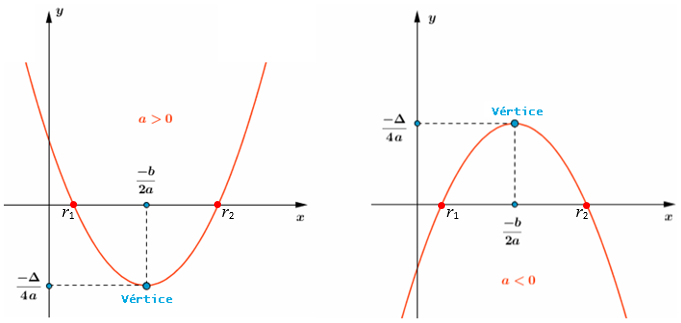
Nos próximos problemas, utilizaremos funções quadráticas para problemas de custo e receita. Antes de passar para os problemas, vamos dar uma revisada: o custo é todo e qualquer valor aplicado no momento da produção do produto. Podemos considerar como custos a mão de obra, a matéria-prima e os insumos utilizados na produção, além da quantia despendida com energia elétrica, manutenção, depreciação de máquinas e equipamentos. Os custos podem ser classificados em fixos e variáveis:
✐ Custos Fixos
Custos fixos são aqueles que não sofrem alteração de valor em caso de aumento ou diminuição da produção. Independem, portanto, do nível de atividade e são conhecidos também como custos de estrutura.
Exemplos: Limpeza e conservação; aluguéis de equipamentos e instalações.
✐ Custos Variáveis
Classificamos como custos variáveis aqueles que variam proporcionalmente, de acordo com o nível de produção ou atividades. Seus valores dependem diretamente do volume produzido ou volume de vendas efetivado num determinado período.
Exemplos: Matérias-primas; insumos produtivos (água, energia).
Agora que já entendemos os “atores” do nosso contexto, vamos aos problemas!
A diretoria de vendas de uma determinada empresa decide que, ao produzir e vender [tex]x[/tex] unidades de certo produto, a receita total das vendas desse produto, em reais, deverá ser [tex]100 \sqrt{x}[/tex]. Se a produção de qualquer quantidade desse produto tem um custo fixo de [tex]R\$\, 1.200,00[/tex] e o custo por unidade produzida é de [tex]R\$ \, 2,00[/tex], para quais valores de [tex]x[/tex] a empresa não terá lucro nem prejuízo, isto é, a receita total das vendas será o custo variável mais o custo fixo?
Uma empresa produz semanalmente [tex]300[/tex] unidades de um determinado produto, quantidade essa que é vendida totalmente ao preço de [tex]600[/tex] reais cada unidade.
Ao longo de um período de tempo observou-se que, se o preço das unidades variava, as vendas também variavam de acordo com a seguinte relação:
- a cada [tex]7[/tex] reais de aumento ou de desconto no preço de cada unidade, a venda diminuía ou aumentava em [tex]3[/tex] unidades, respectivamente.
A partir dessas observações, a que preço a receita seria máxima?
As Parábolas
Conforme explicado acima, o gráfico de uma função quadrática é uma parábola. Você já parou para pensar por que as antenas parabólicas são parabólicas?
Isso envolve a configuração de certos ângulos para que os sinais sejam captados de forma eficaz. Em uma superfície parabólica, um feixe de partículas paralelas ao eixo de simetria é direcionado para o seu foco.
Foco da parábola? Acho que “perdi o foco”.
Calma!
Realmente, até agora, falamos da parábola como o gráfico de uma função quadrática. Mas, existe uma descrição geométrica muito interessante para este objeto matemático. Uma parábola é o lugar geométrico dos pontos que equidistam de um ponto (chamado o foco da parábola) e de uma reta (a diretriz da parábola). Em outras palavras, todos os pontos do plano que têm a mesma distância de um ponto e uma reta dada formam uma parábola:
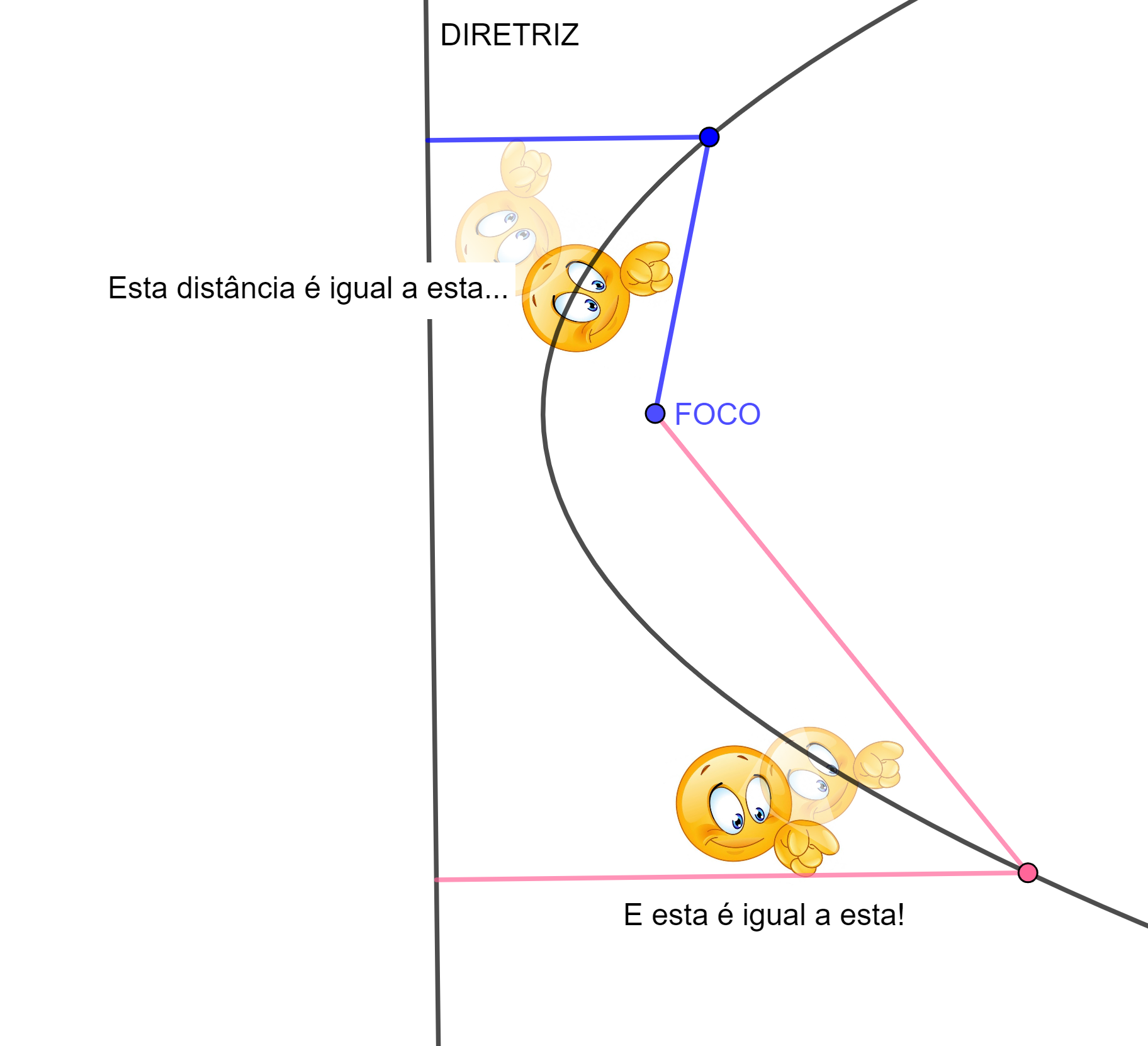
Voltando à propriedade de reflexão, segundo a qual um feixe de partículas paralelas ao eixo de simetria é direcionado para o seu foco, o inverso também vale, isto é, as partículas que saem do foco são refletidas na superfície e projetam um feixe paralelo ao eixo de simetria da parábola. Este é o princípio de funcionamento dos faróis, por exemplo, que são superfícies parabólicas.

Imagem extraída de Parábolas: As curvas misteriosas. Acesso em: jun 2024.
Para entender melhor, nada mais adequado do que assistir a um vídeo do grande professor Elon (falecido em 2017):

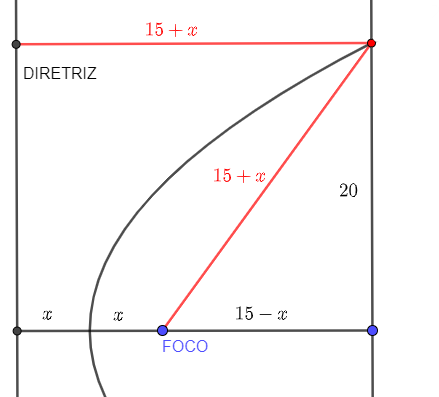
Um refletor parabólico tem [tex]15\text{ cm}[/tex] de profundidade e seu diâmetro é de [tex]40\text{ cm}[/tex]. A que distância está o foco do vértice?
Embora a utilização da equação quadrática na questão acima seja apenas por conta do Teorema de Pitágoras, fica clara a importância da equação quadrática em problemas de geometria envolvendo parábolas, desde que possamos relacionar as duas definições de parábola (a definição algébrica, como o gráfico de uma função quadrática, e a definição geométrica, via foco e diretriz). Mas como encontrar a equação quadrática que define uma parábola dados seu foco e sua diretriz?
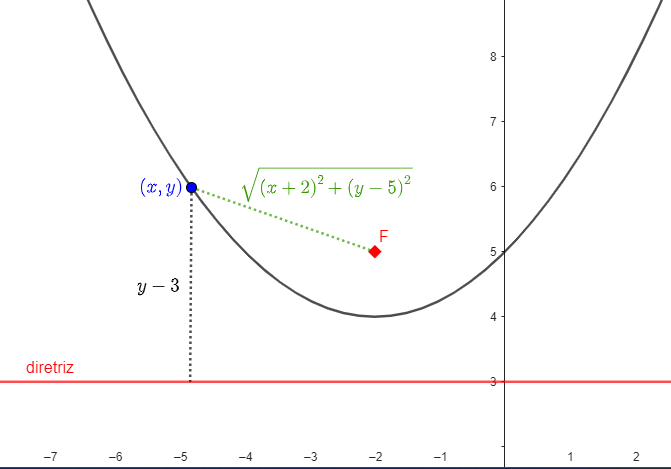
Encontre a função quadrática cujo gráfico é uma parábola com diretriz [tex]y=3[/tex] e foco [tex]F=(-2,5)[/tex]. Você consegue generalizar para uma parábola com diretriz [tex]y=d[/tex] e foco [tex]F=(m,n)[/tex]?
Uma seção transversal de um iniciador de fogo solar com tamanho de viagem é mostrada abaixo:
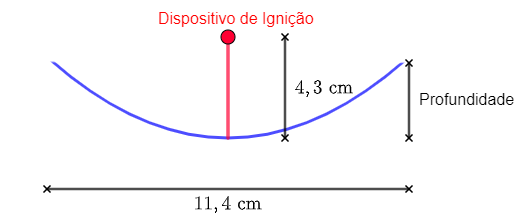
Os raios do sol refletem no espelho parabólico em direção a um objeto preso ao dispositivo de ignição. Como o dispositivo de ignição está localizado no foco da parábola, os raios refletidos fazem com que o objeto queime em apenas alguns segundos.
Supondo que o vértice do espelho parabólico seja a origem do plano cartesiano, encontre a equação da parábola que modela o iniciador de fogo. Use esta equação para encontrar a profundidade do iniciador de fogo.
Atividade em grupo 2
Você verificou na Questão 3 que as equações quadráticas são fundamentais para descrever o movimento vertical de um objeto lançado. Mas se engana se pensa que a equação quadrática para a descrição de movimentos se resume a lançamentos verticais! As parábolas estão intimamente ligadas aos lançamentos oblíquos. Para entender um pouco mais, propomos um experimento para a observação de parábolas a partir de jatos de água.
 Materiais necessários:
Materiais necessários:
- Uma mangueira que forneça um jato contínuo, sem esguichar muita água;
- Trena;
- Transferidor;
- Cronômetro.
Procedimentos:
- Regular o fluxo de água que sai pela mangueira (cuidado com o desperdício!);
- Para melhor percepção, sugere-se que o experimento seja realizado próximo de uma parede, onde deve ser marcada a posição inicial (origem) e os ângulos ([tex]90^\circ[/tex], [tex]75^\circ[/tex], [tex]60^\circ[/tex], [tex]45^\circ[/tex], [tex]30^\circ[/tex] e [tex]15^\circ[/tex]);
- Para cada ângulo, medir o tempo ([tex]t[/tex]) necessário para o jato retornar ao solo e o alcance ([tex]A[/tex]);
- O experimento pode ser filmado e exibido em câmera lenta para melhor observação;
- Para cada ângulo, escrever uma função matemática que descreve o movimento da água (altura x tempo), construir os gráficos (manualmente ou com o uso do computador), e discutir os resultados.
- Pesquisar sobre a fórmula do alcance, com a ajuda de seus professores de matemática e de física.
Na próxima Sala, vamos mostrar como as equações quadráticas auxiliam em problemas reais relativos ao estudo do espaço.
- Applications of Quadratic Equations (toppr)
- Applications of Quadratic Functions (lumen)
- Application Problems with Quadratic Equations (Whitmore School)
- Chung, K. A parábola, sua propriedade refletora e aplicações. Trabalho de Conclusão-Departamento de Matemática da Universidade Federal Rural de Pernambuco, 32.
- Fresnel Lens and Parabolic Reflectors (Parabolix)
- “Modelagem Matemática no Ensino de Funções Polinomiais do 2º Grau” em Só Pedagogia. Virtuous Tecnologia da Informação, 2008-2023. Disponível em http://www.pedagogia.com.br/artigos/modelagemmatematica/index.php.
- Parabolic Mirror (Isaac Physics)
- Quadratic Equations in Real Life (Study.com)
- Real World Examples of Quadratic Equations (Math is Fun)
- Study STEM @ SCC
- O que é aceleração? (Khan Academy)
- O que é deslocamento? (Khan Academy)
- O que é velocidade vetorial média? (Khan Academy)
- Revisão do foco e diretriz da parábola (Khan Academy)
- Uses of quadratic equations in daily life (All uses of)
- Movimento uniforme (Brasil Escola)