M_Sala de ajuda: Funções – Composição, uma operação especial

Funções

Composição, uma operação especial

Embora definidas de modo bem natural, as operações adição, subtração, multiplicação e divisão entre funções têm o inconveniente de exigirem condições especiais dos contradomínios das funções que serão utilizadas: respectivamente, a soma, a diferença, o produto e o quociente entre elementos dos contradomínios devem estar definidos.
Apresentaremos agora uma operação que pode ser definida sem a necessidade de que os elementos dos contradomínios das funções envolvidas tenham alguma outra propriedade que não a de “ser elementos do contradomínio”.
De maneira informal, considere duas funções [tex]f: A \rightarrow B [/tex] e [tex]g: B \rightarrow C [/tex].

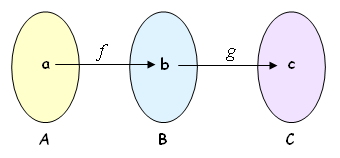
Poderíamos relacionar os elementos do conjunto [tex]A[/tex] e do conjunto [tex]C[/tex] sem a intermediação do conjunto [tex]B[/tex] e definirmos uma terceira função, digamos [tex]h[/tex], [tex]h: A \rightarrow C [/tex], conforme mostra o esquema a seguir.

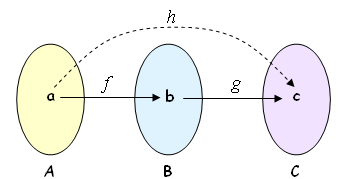
Como poderíamos definir [tex]h[/tex], a partir de [tex]f[/tex] e de [tex]g[/tex]?

Observe: [tex]\boxed{h(a)=c=g\left(b\right)=g\left(f\left(a\right)\right)}[/tex]. E para não esquecermos de que [tex]h[/tex] foi definida a partir de [tex]f[/tex] e de [tex]g[/tex]:

denotaremos [tex]h[/tex] por [tex]g\circ f[/tex];
denominaremos [tex]h[/tex] de "composta de [tex]g[/tex] e [tex]f[/tex]".

Formalmente, temos a seguinte definição:

Sejam [tex]f: A \rightarrow B [/tex] e [tex]g: B \rightarrow C [/tex] funções.
Chamamos de função composta de [tex]g[/tex] e [tex]f[/tex] a função de [tex]A[/tex] em [tex]C[/tex] dada por [tex]y=g\left(f\left(x\right)\right)[/tex].
É usual utilizar a notação [tex]g\circ f[/tex] para representar a composta de [tex]g[/tex] e [tex]f[/tex].
Assim:

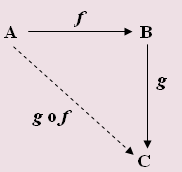
[tex]\qquad g\circ f: A \rightarrow B \\ \qquad \qquad \left(g\circ f\right) \left(x\right)=g\left(f\left(x\right)\right).[/tex]

A composta [tex] g\circ f[/tex] é também chamada de:

g bola f;
gof.

Exemplos

✐ Sejam [tex]f: \mathbb{R} \rightarrow \mathbb{R} [/tex] e [tex]g: \mathbb{R} \rightarrow \mathbb{R} [/tex] as funções dadas por [tex]f(x) = 4x[/tex] e [tex]g(x) = x+5[/tex]. Então:
(a) [tex]g \circ f: \mathbb{R} \rightarrow \mathbb{R} [/tex] é assim definida:
[tex](g \circ f)(x) = g(f(x))= g(4x) = (4x) + 5 = 4x + 5[/tex].

(b) Neste caso, podemos também definir a composta de [tex]f[/tex] e [tex]g[/tex]
[tex]f \circ g: \mathbb{R} \rightarrow \mathbb{R} [/tex] é assim definida:
[tex](f \circ g)(x) = f(g(x))= f(x + 5) = 4(x + 5)=4x+ 20[/tex].

✐ Sejam [tex]f: \mathbb{R} \rightarrow \mathbb{R} [/tex] e [tex]g: \mathbb{R} \rightarrow \mathbb{R} [/tex] as funções dadas por [tex]f(x) = x^2+1[/tex] e [tex]g(x) = 2x[/tex].
Clique na setinha e veja como calcular as regras que definem as compostas [tex]g \circ f[/tex], [tex]f \circ g[/tex] e [tex]f \circ f[/tex].

Refinando a definição

Podemos enfraquecer as condições para definirmos a composta de duas funções, conforme veremos a seguir.
Observe que se temos funções [tex]f[/tex] e [tex]g[/tex] tais que [tex]f: A \rightarrow B [/tex] e [tex]g: B \rightarrow C [/tex], podemos calcular a imagem [tex] \left(g\circ f\right) \left(x\right)[/tex] como definimos: [tex] \boxed{\left(g\circ f\right) \left(x\right)=g\left(f\left(x\right)\right)}[/tex].
Na verdade, a condição de que o domínio da [tex]g[/tex] seja igual ao contradomínio da [tex]f[/tex] é uma condição suficiente para que possamos calcular [tex]g\left(f\left(x\right)\right)[/tex], mas não é uma condição necessária para isso. Perceba que só precisamos que a função [tex]g[/tex] esteja definida para o elemento [tex]f(x)[/tex] para que possamos calcular [tex]g\left(f\left(x\right)\right)[/tex]; e como sabemos que [tex]f(x) \in Im\left(f\right)[/tex], então basta que [tex] Im\left(f\right)[/tex] esteja contida no domínio da função [tex]g[/tex] para que seja possível se definir a composta [tex]g\circ f[/tex], de acordo com a regra apresentada. Veja, então, uma definição mais geral da composta [tex]g\circ f[/tex].

Sejam [tex]f: A \rightarrow B [/tex] e [tex]g: C \rightarrow D [/tex] funções tais que [tex] Im\left(f\right)\subset C[/tex].
Chamamos de função composta de [tex]g[/tex] e [tex]f[/tex] a função de [tex]A[/tex] em [tex]D[/tex] dada por [tex]y=g\left(f\left(x\right)\right)[/tex].
Assim:
[tex]\qquad g\circ f: A \rightarrow D \\ \qquad \qquad \left(g\circ f\right) \left(x\right)=g\left(f\left(x\right)\right).[/tex]

Um vídeo para ajudar…

Para assistir, é só clicar na setinha.

Um texto para ajudar…

Para que você exercite a primeira definição de composição, deixamos aqui algumas páginas do volume 1 da excelente coleção Fundamentos de Matemática Elementar.

Para ler o material, clique no próximo botão.

Ler o material

Para copiar o material, clique no botão abaixo.

Baixar o arquivo

Bons estudos!