Funções
Operações
Um tipo importante de função são as chamadas operações. Talvez vocês nem soubessem que as operações que vocês conhecem são funções, mas vamos pensar um pouco. Tomemos como base dois conjuntos numéricos bem conhecidos: [tex]\mathbb{N}[/tex], o conjunto dos números naturais, e [tex]\mathbb{Z}[/tex], o conjunto dos números inteiros. Vamos observar a adição em [tex]\mathbb{N}[/tex] e em [tex]\mathbb{Z}[/tex], a multiplicação em [tex]\mathbb{N}[/tex] e em [tex]\mathbb{Z}[/tex] e a subtração em [tex]\mathbb{Z}[/tex]:
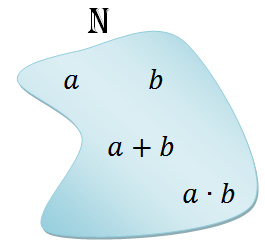
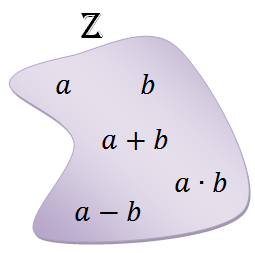
Olhando dessa forma, o conceito de função fica, de fato, escondido, mas o que fazem essas operações nesses dois conjuntos?
(1) (2)
(3) (4)(5)
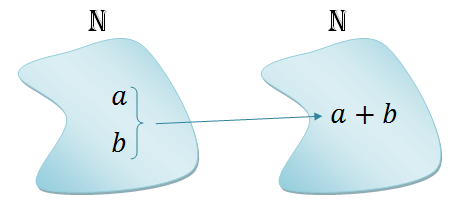
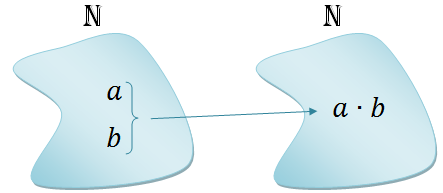
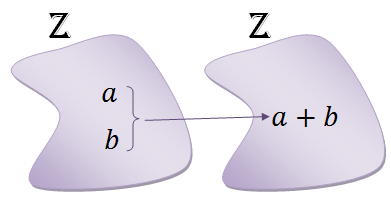
Talvez os diagramas acima ajudem a entender que:
(1) A adição em [tex]\mathbb{N}[/tex] é uma função de [tex]\mathbb{N} \times \mathbb{N}[/tex] em [tex]\mathbb{N}[/tex] que a cada par ordenado de números naturais [tex](a,b)[/tex] associa a soma [tex]a+b:[/tex]
[tex]\begin{align*} +: \mathbb{N} \times \mathbb{N} &\rightarrow \mathbb{N} \\ (a,b) &\mapsto a+b \end{align*}[/tex]
(2) A multiplicação em [tex]\mathbb{N}[/tex] é uma função de [tex]\mathbb{N} \times \mathbb{N}[/tex] em [tex]\mathbb{N}[/tex] que a cada par ordenado de números naturais [tex](a,b)[/tex] associa o produto [tex]a\times b[/tex]:
[tex]\begin{align*} \times: \mathbb{N} \times \mathbb{N} &\rightarrow \mathbb{N} \\ (a,b) &\mapsto a\times b \end{align*}[/tex]
(3) A adição em [tex]\mathbb{Z}[/tex] é uma função de [tex]\mathbb{Z} \times \mathbb{Z}[/tex] em [tex]\mathbb{Z}[/tex] que a cada par ordenado de números inteiros [tex](a,b)[/tex] associa a soma [tex]a+b[/tex]:
[tex]\begin{align*} +: \mathbb{Z} \times \mathbb{Z} &\rightarrow \mathbb{Z} \\ (a,b) &\mapsto a+b \end{align*}[/tex]
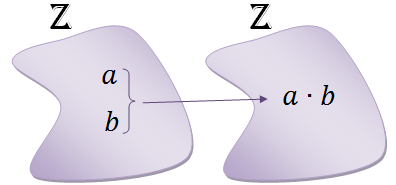
(4) A multiplicação em [tex]\mathbb{Z}[/tex] é uma função de [tex]\mathbb{Z} \times \mathbb{Z}[/tex] em [tex]\mathbb{Z}[/tex] que a cada par ordenado de números inteiros [tex](a,b)[/tex] associa o produto [tex]a\times b[/tex]:
[tex]\begin{align*} \times: \mathbb{Z} \times \mathbb{Z} &\rightarrow \mathbb{Z} \\ (a,b) &\mapsto a\times b \end{align*}[/tex]
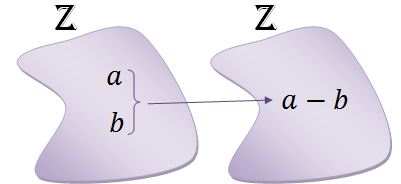
(5) A subtração em [tex]\mathbb{Z}[/tex] é uma função de [tex]\mathbb{Z} \times \mathbb{Z}[/tex] em [tex]\mathbb{Z}[/tex] que a cada par ordenado de números inteiros [tex](a,b)[/tex] associa a diferença [tex]a – b[/tex]:
[tex]\begin{align*} -: \mathbb{Z} \times \mathbb{Z} &\rightarrow \mathbb{Z} \\ (a,b) &\mapsto a – b \end{align*}[/tex]
Já temos, então, cinco exemplos do que definiremos abaixo como uma operação em um conjunto [tex]A[/tex].
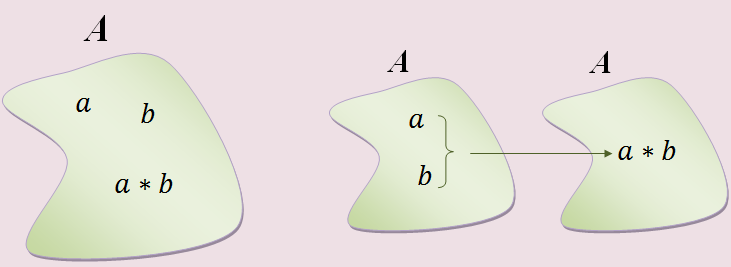
Chamamos de operação em [tex]A[/tex] a toda função * de [tex]A\times A[/tex] em [tex]A[/tex]. É comum representar a imagem de um par ordenado [tex](a,b)[/tex] pela função * por [tex]a*b[/tex]. Assim, é utilizada a seguinte notação para indicar uma operação em um conjunto [tex]A[/tex].
Notação:
[tex]\begin{align*} *: \mathbb{A} \times \mathbb{A} &\rightarrow \mathbb{A} \\ (a,b) &\mapsto a * b \end{align*}[/tex]
Operações entre funções
Sejam [tex]A[/tex] e [tex]B[/tex] conjuntos não vazios e [tex]E[/tex] o conjunto de todas as funções de [tex]A[/tex] em [tex]B[/tex]:
[tex]E=\{f: A \rightarrow B, f \, [/tex] função[tex]\}[/tex].
Se em [tex]B[/tex] estiver definida uma soma, um produto, uma diferença ou um quociente podemos definir em [tex]E[/tex] somas, produtos, diferenças e quocientes de funções, de acordo com as definições a seguir.
✐ Chamamos de soma de [tex]f[/tex] e [tex]g[/tex] a função denotada por [tex]f+g[/tex] e assim definida:
[tex]\begin{align*} f+g: \, & A \rightarrow B\\ & \left( f+g \right)(x)=f(x)+g(x) \end{align*}[/tex]
✐ Chamamos de produto de [tex]f[/tex] e [tex]g[/tex] a função denotada por [tex]f\cdot g[/tex] e assim definida:
[tex]\begin{align*} f\cdot g: \, & A \rightarrow B\\ & \left( f\cdot g \right)(x)=f(x)\times g(x) \end{align*}[/tex]
✐ Chamamos de diferença de [tex]f[/tex] e [tex]g[/tex] a função denotada por [tex]f – g[/tex] e assim definida:
[tex]\begin{align*} f-g: \, & A \rightarrow B\\ & \left( f – g \right)(x)=f(x) – g(x) \end{align*}[/tex]
✐ Chamamos de quociente de [tex]f[/tex] e [tex]g[/tex] a função denotada por [tex]\dfrac{f}{g}[/tex] e assim definida:
[tex]\begin{align*}\frac{f}{g}: \, & A \rightarrow B\\ & \left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)} \end{align*}[/tex]
Como em [tex]\mathbb{R}[/tex] podemos definir a soma, a diferença e o produto entre dois números reais quaisquer e também o quociente entre dois números reais [tex]a[/tex] e [tex]b[/tex], com [tex]b\ne 0[/tex], podemos definir somas, diferenças e produtos de funções de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex] e quocientes [tex]\dfrac{f}{g}[/tex] de funções de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex] tais que [tex]g(x) \ne 0[/tex].
É possível definirmos operações entre funções exigindo um pouco menos de condições. Vejam as definições das operações apresentadas no livro Um curso de Cálculo – volume 1; Hamilton Luiz Guidorizzi.
Para copiar o material, clique no botão abaixo.
Bons estudos!
 |
Precisam de exercícios? |
Equipe COM – OBMEP
