.Números especiais – pares e ímpares

Onde tudo começa…

O conjunto dos múltiplos naturais de [tex] \, 2 \, [/tex], [tex]\{0, \, 2, \, 4, \, 6, \, 8, \, \cdots \, \}[/tex], define uma categoria importante e muito antiga de números naturais: os números naturais pares. Um número natural [tex]n[/tex] é dito par se [tex]n[/tex] for um múltiplo de [tex]2[/tex]; assim temos formalmente a seguinte definição:

Definição: Um número natural [tex]n[/tex] é dito par se existir um número natural [tex]k[/tex] de modo que [tex]n=2k[/tex].
Um número natural que não seja par chama-se ímpar.

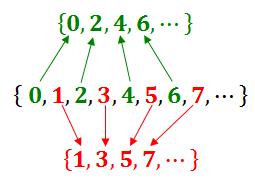
Se denotarmos o conjunto dos números naturais pares por [tex]\mathbb{P}[/tex] e o conjunto dos números naturais ímpares por [tex]\mathbb{I}[/tex], então [tex]\mathbb{I}[/tex] será constituído pelos números naturais que não são pares e, assim, [tex]\mathbb{P}=\{0, \, 2, \, 4, \, 6, \, 8, \, \cdots \, \} \, \, [/tex] e [tex] \, \, \mathbb{I}=\{ \, 1, \, 3, \, 5, \, 7, \, 9, \, \cdots \, \}[/tex].

Perde-se no tempo a classificação dos números naturais em pares e ímpares. Na Grécia Antiga, essa classificação já aparece na Escola Pitagórica, por volta de 500 anos a.C., e com uma interpretação muito próxima da que utilizaremos como definição. De acordo com a concepção pitagórica:

par é o número que pode ser dividido em duas partes iguais, sem que uma unidade fique no meio; e ímpar é aquele que não pode ser dividido em duas partes iguais, porque sempre há uma unidade no meio.

Caracterização dos números naturais ímpares

Inicialmente, vamos mostrar que não podemos caracterizar os naturais ímpares como múltiplos de um determinado número natural, pois tal número não existe.

Justificativa: Claramente [tex]1[/tex] não é par ( [tex]2\times 0=0\lt 1\lt 2=2\times1\lt 4=2\times 2\lt\cdots)[/tex], logo é ímpar. Por outro lado, o único número natural do qual [tex]1[/tex] é múltiplo é o próprio [tex]1[/tex]. Assim, se todos os ímpares fossem múltiplos de um determinado número natural, esse número deveria ser [tex]1[/tex]. Mas notem que todos os pares também são múltiplos de [tex]1[/tex]; logo ser múltiplo de [tex]1[/tex] não é uma característica exclusiva dos ímpares e, portanto, não podemos dizer que os ímpares são aqueles números naturais que são múltiplos de [tex]1[/tex], pois os pares igualmente o são.

Tentemos, então, outra caracterização.

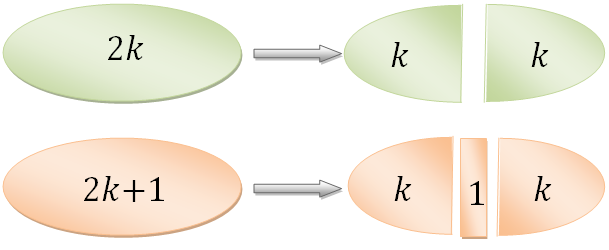
Percebam que as formas [tex]n=2k \, [/tex] e [tex] \, n=2k+1[/tex] mostram claramente as ideias pitagóricas de que “par é o número que pode ser dividido em duas partes iguais, sem que uma unidade fique no meio“, e “ímpar é o número que não pode ser dividido em duas partes iguais, porque sempre há uma unidade no meio“.

Paridade em [tex]\mathbb{N}[/tex] e sua aritmética

Observem que, no box anterior, mais do que mostrar que

● [tex]n[/tex] é um número natural par se, e somente se, [tex]n=2k[/tex], para algum número natural [tex]k[/tex];
● [tex]n[/tex] é um número natural ímpar se, e somente se, [tex]n=2k+1[/tex], para algum número natural [tex]k[/tex];

mostramos que todo número natural assume uma e apenas uma destas formas: [tex]n=2k[/tex] ; [tex]n=2k+1[/tex], com [tex]k\in\mathbb{N}[/tex]. Dessa maneira, temos que:

[tex]\qquad\qquad\boxed{\mathbb{N}= \mathbb{P} \cup \mathbb{I}}[/tex], com [tex]\boxed{\mathbb{P} \cap \mathbb{I}=\emptyset}[/tex].

Devido a essas duas características, podemos utilizar linguagem matemática específica da Teoria de Conjuntos e dizer que [tex]\{\mathbb{P} \, ; \, \mathbb{I} \}[/tex] é uma partição de [tex]\mathbb{N}[/tex]. Na prática isso significa que, dado um número natural [tex]x[/tex], [tex]x[/tex] é par ou [tex]x[/tex] é ímpar e somente uma dessas duas opções.
Assim, faz sentido a discussão que apresentaremos a seguir.

A partir da paridade de dois números naturais, podemos determinar a paridade da soma e do produto desses números, sem sequer conhecê-los. Essas são características que ajudam na solução de vários problemas, então vale a pena conhecê-las.

Aritmética da paridade

---

Propriedade 1 (Paridade da soma): (a) A soma de dois números naturais de mesma paridade é par. (b) A soma de dois números naturais de paridade oposta é ímpar.	Propriedade 2 (Paridade do produto): O produto de dois números naturais só será ímpar se os dois números forem ímpares.
● par + par = par ● ímpar + ímpar = par ● par + ímpar = ímpar ● ímpar + par = ímpar	● par x par = par ● par x ímpar = par ● ímpar x par = par ● ímpar x ímpar = ímpar

Podemos utilizar essas duas propriedades para obter outras igualmente interessantes e importantes. Se você quiser resolver problemas sobre a aritmética da paridade, é só clicar [tex] \, \fcolorbox{#77ae52}{#77ae52}{AQUI} \, [/tex].

Estendendo o conceito de paridade

Se tomarmos o conjunto dos naturais pares e acrescentarmos para cada número par o seu respectivo oposto obteremos o seguinte subconjunto dos inteiros:
[tex]\qquad\qquad \{0, \, 2, \, 4, \, 6, \, 8, \, \cdots \, \}\longrightarrow \{0, \, 2,-2, \, 4,-4, \, 6,-6, \, 8,-8, \, \cdots \, \}[/tex]
que tradicionalmente é escrito como
[tex]\qquad\qquad \{ \, \cdots ,-8,-6,-4,-2, \, 0, \, 2, \, 4, \, 6, \, 8, \, \cdots \, \}[/tex]
e cujos elementos podem ser escritos na forma [tex] \, n=2k[/tex], com [tex]k\in\mathbb{Z}[/tex].
De modo análogo, se ao conjunto dos naturais ímpares acrescentarmos para cada número o seu respectivo oposto obteremos o seguinte subconjunto de [tex]\mathbb{Z}[/tex]:
[tex]\qquad\qquad \{1, \, 3, \, 5, \, 7, \, \cdots \, \}\longrightarrow \{1,-1, \, 3,-3, \, 5,-5, \, 7,-7, \, \cdots \, \}[/tex]
que tradicionalmente é escrito como
[tex]\qquad\qquad \{ \, \cdots ,-7,-5,-3,-1, \, 1, \, 3, \, 5, \, 7, \, \cdots \, \}[/tex]
e cujos elementos podem ser escritos na forma [tex] \, n=2k+1[/tex], com [tex]k\in\mathbb{Z}[/tex].
Os dois conjuntos obtidos serão denominados conjunto dos inteiros pares e conjunto dos inteiros ímpares, respectivamente.
Nesta derradeira discussão, vamos utilizar as seguintes notações para os quatro conjuntos de pares e ímpares:
[tex]\quad \mathbb{P}=\{ \, \cdots ,-8,-6,-4,-2, \, 0, \, 2, \, 4, \, 6, \, 8, \, \cdots \, \}[/tex] (inteiros pares);
[tex]\quad \mathbb{P_\mathbb{N}}=\{0, \, 2, \, 4, \, 6, \, 8, \, \cdots \, \}[/tex] (naturais pares);
[tex]\quad \mathbb{I}=\{ \, \cdots ,-7,-5,-3,-1, \, 1, \, 3, \, 5, \, 7, \, \cdots \, \}[/tex] (inteiros ímpares);
[tex]\quad \mathbb{I_\mathbb{N}}=\{1, \, 3, \, 5, \, 7, \, \cdots \, \}[/tex] (naturais ímpares).

Como:

(1) [tex] \mathbb{P}\subset\mathbb{Z}[/tex];
(2) [tex] \mathbb{I}\subset\mathbb{Z}[/tex];
(3) [tex] \mathbb{P}\cap\mathbb{I}=\emptyset[/tex];
(4) [tex] \mathbb{P}\cup\mathbb{I}=\mathbb{Z}[/tex];

então [tex]\{\mathbb{P} \, ; \, \mathbb{I}\}[/tex] é uma (bi)partição de [tex] \mathbb{Z}[/tex].
Com base no até aqui exposto, em nossas discussões, podemos estender o conceito de paridade e adotar as seguintes definições:

Definições:
● Um número inteiro [tex]m[/tex] é dito par se existir um número inteiro [tex]t[/tex] de modo que [tex]m=2t[/tex].
● Um número inteiro [tex]m[/tex] é dito ímpar se existir um número inteiro [tex]t[/tex] de modo que [tex]m=2t+1[/tex].
● Diremos que os números inteiros (ou naturais) [tex]a \, [/tex] e [tex] \, b[/tex] têm a mesma paridade se forem ambos pares ou ambos ímpares. Caso contrário, dizemos que [tex]a \, [/tex] e [tex] \, b[/tex] têm paridade oposta.

A paridade da soma e a paridade do produto podem, também, ser estendidas para o conjunto dos números inteiros.

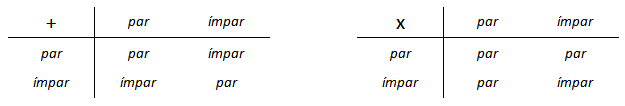
As demonstrações dessas propriedades são idênticas às demonstrações feitas nesta página , bastando, apenas, observar que:
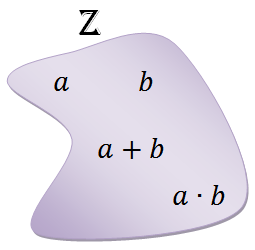
● A soma de números inteiros é sempre um número inteiro.
● O produto de números inteiros é sempre um número inteiro.
ou seja, o conjunto dos números inteiros é também fechado com relação à adição e à multiplicação.

Mais do que isso, como em [tex]\mathbb{Z}[/tex] podemos definir diferenças sem restrições e toda diferença de números inteiros pode ser vista como uma soma: [tex]a-b=a+(-b)[/tex], então a diferença em [tex]\mathbb{Z}[/tex] herda as propriedades da paridade da soma dos inteiros.

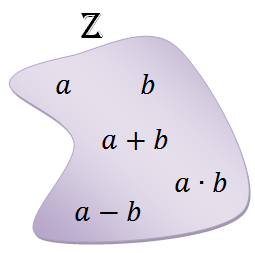
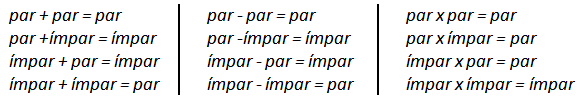
Que tal vocês tentarem demonstrar a paridade da soma, da diferença e do produto de inteiros, fazendo as devidas adaptações nas demonstrações feitas nesta página? É um bom exercício!