.Brincando com Geometria: Mediatriz de um segmento

O que é mesmo a mediatriz de um segmento?

Mas afinal de contas, uma mediatriz é uma reta ou um lugar geométrico?

Por mais estranho que pareça, as duas coisas  . . .

Como assim ? ! ? ! ? ! ? ! ?

Calma, vou tentar explicar. . .

Na planilha abaixo, fixamos um segmento [tex]\overline{AB}[/tex] e traçamos a reta perpendicular a esse segmento e que passa pelo seu ponto médio (a reta que definimos como mediatriz). Com essa planilha você poderá observar que os pontos dessa reta são equidistantes dos pontos [tex] A[/tex] e [tex]B[/tex].

Na próxima planilha, fixamos um segmento [tex]\overline{AB}[/tex] e traçamos a reta perpendicular a esse segmento e que passa pelo ponto médio do segmento (a reta que definimos como mediatriz). Definimos pares de circunferências de centros em [tex]A[/tex] e [tex]B[/tex], ambas com raios iguais (variando de [tex]3,2 \, [/tex]cm a [tex]8 \, [/tex]cm), de modo a obtermos pontos equidistantes de [tex]A[/tex] e de [tex]B[/tex]: com efeito, se duas circunferências têm o mesmo raio, os pontos de interseção delas, quando existirem, são equidistantes de seus centros, no nosso caso, os pontos [tex]A[/tex] e [tex]B[/tex].
O que poderemos observar é que todos os pontos de interseção determinados pertencem à reta definida como a mediatriz do segmento.

Mais uma coisa: o que significa “A planilha ajuda na visualização do resultado; mas, matematicamente, não substitui sua demonstração“?

Com as planilhas podemos verificar que os pontos da reta que definimos como mediatriz do segmento [tex]\overline{AB}[/tex] são equidistantes dos pontos [tex]A[/tex] e [tex]B[/tex] e, reciprocamente, que os pontos que são equidistantes de [tex]A[/tex] e [tex]B[/tex] pertencem à reta que definimos como mediatriz do segmento [tex]\overline{AB}[/tex] APENAS para alguns pontos de um segmento particular [tex]\overline{AB}[/tex]. Mas não há como fazer essa verificação em todas as situações possíveis de pontos e segmentos. Assim temos que fazer uma justificativa genérica, ou seja, fazer o que chamamos na Matemática de demonstração.

A demonstração:

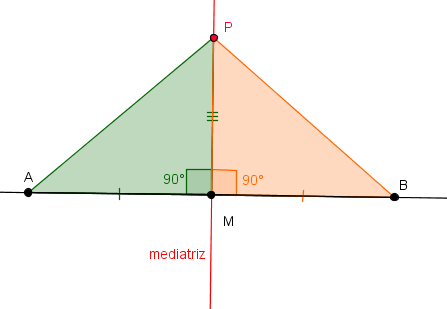
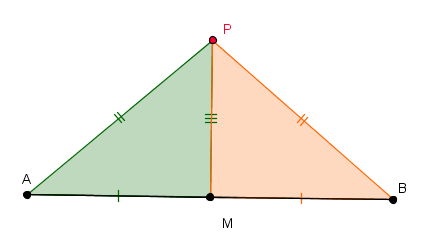
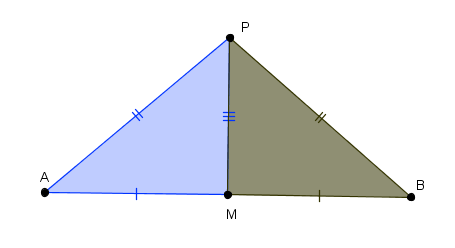
Fixe um plano [tex]\alpha[/tex] e considere nesse plano um segmento de reta [tex]\overline{AB}[/tex] cujo ponto médio denotaremos por [tex]M[/tex]. Vamos mostrar que a reta perpendicular a esse segmento e que passa pelo seu ponto médio é o lugar geométrico dos pontos do plano [tex]\alpha[/tex] que equidistam de [tex]A[/tex] e de [tex]B[/tex].
Como um lugar geométrico é um conjunto de pontos, tal como uma reta, estamos propondo mostrar que, fixado um plano [tex]\alpha[/tex], dois conjuntos de pontos desse plano são iguais. Para isso, devemos mostrar que todo ponto de cada um dos conjuntos é também ponto do outro.
Dessa forma, fixemos um plano [tex]\alpha[/tex], fixemos dois pontos distintos desse plano, [tex]A[/tex] e [tex]B[/tex], e consideremos os seguintes conjuntos:
 
[tex]\qquad m:[/tex] reta do plano [tex]\alpha[/tex] que é perpendicular ao segmento [tex]\overline{AB}[/tex] e que passa pelo ponto médio [tex] M [/tex] desse segmento;
        (a reta que definimos como mediatriz desse segmento)
 
[tex]\qquad l[/tex]: conjunto dos pontos do plano [tex]\alpha[/tex] que equidistam de [tex]A[/tex] e [tex]B[/tex].
 
Mostraremos que os conjuntos [tex]m[/tex] e [tex]l[/tex] são iguais, isso é, mostraremos que:
 
    (i) todo elemento de [tex]m[/tex] é elemento de [tex]l[/tex] e
 
    (ii) todo elemento de [tex]l[/tex] é elemento de [tex]m[/tex].
 
Vamos lá:

(i) Tomemos, inicialmente, um ponto [tex]P[/tex] qualquer da reta [tex]m[/tex].
[tex]\bullet[/tex] Se [tex]P=M[/tex], então [tex]P[/tex] é o ponto médio de [tex]\overline{AB}[/tex]. Assim, por definição de ponto médio, [tex]d(P,A)=d(P,B)[/tex], logo [tex]P \in l[/tex].
[tex]\bullet[/tex] Consideremos, agora, que [tex]P[/tex] não seja o ponto médio de [tex]\overline{AB}[/tex], isto é, que [tex]P\neq M [/tex].
Tracemos os segmentos [tex]\overline{PA}[/tex] e [tex]\overline{PB}[/tex] e consideremos os seguintes triângulos: [tex]\Delta PAM[/tex] e [tex]\Delta PBM[/tex].
Observamos que os triângulos definidos são congruentes, pelo caso lado-ângulo-lado.

Como [tex]\Delta PAM \cong \Delta PBM[/tex], em particular temos que os segmentos [tex]\overline{PA}[/tex] e [tex]\overline{PB}[/tex] são congruentes.

Dessa forma, [tex]d(P,A)=d(P,B)[/tex], donde temos que [tex]P \in l[/tex].

          Pelo exposto, todo ponto de [tex]m[/tex] é ponto de [tex]l[/tex] ([tex]m \subset l[/tex]).
 
(ii) Tomemos, agora, um ponto [tex]P[/tex] qualquer de [tex]l[/tex]; assim [tex]P[/tex] equidista dos pontos [tex]A[/tex] e [tex]B[/tex], isto é, [tex]d(P,A)=d(P,B)[/tex].
[tex]\bullet[/tex] Se [tex]P[/tex] for o ponto médio do segmento [tex]\overline{AB}[/tex], então, necessariamente, [tex]P \in m[/tex], pela definição da reta [tex]m[/tex].
[tex]\bullet[/tex] Suponhamos que [tex]P[/tex] não seja o ponto médio do segmento [tex]\overline{AB}[/tex] e tracemos os segmentos [tex]\overline{PA}[/tex] e [tex]\overline{PB}[/tex].
Podemos observar que os triângulos [tex]\Delta PAM[/tex] e [tex]\Delta PBM[/tex] são congruentes, pelo caso lado-lado-lado,

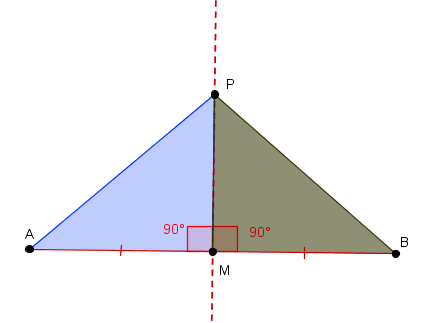
e portanto os ângulos [tex]\angle PMA[/tex] e [tex]\angle PMB[/tex] são congruentes, isto é, têm a mesma medida: [tex]m\angle PMA = m\angle PMB[/tex].
Mas esses ângulos são suplementares, assim [tex]m\angle PMA + m\angle PMB=180^{\circ}[/tex], donde [tex]m\angle PMA = m\angle PMB=90^{\circ}[/tex].
Dessa forma, observamos duas características da reta definida pelos pontos [tex]P[/tex] e [tex]M[/tex], aqui denominada [tex]r[/tex]:
[tex]\diamond \, \, \, \, M \in r[/tex]
[tex]\diamond \, \, \, \, r[/tex] é perpendicular ao segmento [tex]\overline{AB}[/tex]
Portanto a reta [tex]r[/tex] determinada pelos pontos [tex]P[/tex] e [tex]M[/tex] é a própria mediatriz do segmento [tex]\overline{AB}[/tex] e, consequentemente, [tex]P \in m[/tex].

          Dessa forma, todo ponto de [tex]l[/tex] é também ponto de [tex]m[/tex] ([tex]l \subset m[/tex]).

Finalmente, por (i) e por (ii) concluímos que [tex]m = l[/tex].

Dessa forma, fixado um plano [tex]\alpha[/tex], podemos definir a mediatriz de um segmento como “a reta perpendicular ao segmento e que passa pelo seu ponto médio” ou como “o lugar geométrico dos pontos do plano equidistantes das extremidades desse segmento”.

Agora sim !!!!