Tópicos
I – Apresentação do Tema
|
Do número nasce a proporção…….. Da proporção se segue à consonância …….. A consonância causa deleitação …….. A nenhum sentido apraz a dissonância …….. Unidade, igualdade e semelhança …….. São princípios do contentamento…….. Em todos os sentidos o experimento…….. A alma na unidade glória alcança…….. Em todas as quantidades a igualdade …….. E a perfeição remota ou a mais chegada…….. Segundo a natural autoridade…….. E assim está nas qualidades assentada…….. Da mesma maneira a semelhança…….. Diva de ser sentida e contemplada…….. Poema: O misterioso número de ouro |
Encontrada na ciência e na natureza, em diferentes formas, na obra de artistas como Salvador Dalí, de arquitetos como Le Corbusier e na arquitetura de forma geral, a razão áurea é um dos números mais famosos da matemática, há muito tempo – os gregos antigos já atribuíam a essa razão propriedades mágicas e usavam-na nas construções de seus edifícios.
A razão áurea é um número irracional, tal qual o famoso número [tex]\pi[/tex] (pi), e é também denotado por uma letra grega, o “phi” (pronunciamos fi): phi maiúsculo, [tex]\Phi[/tex], ou phi minúsculo, [tex]\varphi[/tex].
Conhecido desde a Antiguidade, o [tex]\Phi[/tex] recebeu vários títulos honoríficos: “Número Áureo”, “Razão Áurea”, “Seção Áurea”, “Proporção Áurea”, “Proporção de Ouro”, “Número de Ouro”, “Média e Extrema Razão”, “Divisão de Extrema Razão”, “Razão de Phidias” e até “Proporção Divina”, tal o fascínio que esse número exerceu sobre as pessoas!
Talvez seja difícil imaginar um número que apareça em situações tão diferentes – artes, ciências, natureza – mas, embora chegue até a ser denominado de Proporção Divina, a razão áurea é apenas um número e uma bela oportunidade de se estudar matemática!
E é com esse espírito que apresentamos o objeto central desta Sala de Atividades: [tex]\Phi[/tex]
Esse famoso objeto matemático aqui será tratado cercado de algumas de suas verdades e de alguns de seus mitos, já que nem tudo o que encontramos sobre esse número é verdadeiro!
Portanto, peguem papel, lápis, borracha e uma lupa, e mãos à obra.
Boa investigação e boa diversão!!!
II – Um pouco de matemática para começar . . .
Um problema inicial
Determinar um número positivo tal que a diferença entre seu quadrado e ele seja 1.
A equação [tex]X^2-X-1=0[/tex], resultante da modelagem desse problema, fornece respostas para alguns problemas geométricos interessantes. Observem dois deles.
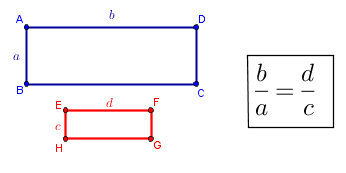
(i) Determinar a distância entre os pontos [tex]A[/tex] e [tex]X[/tex] de forma que a razão entre os comprimentos do menor e do maior dos segmentos seja igual à razão entre os comprimentos do maior e do segmento todo.
(ii) Determinar a razão entre os comprimentos do maior e do menor segmento.
O segundo problema trata de retângulos semelhantes. Se vocês sabem quando dois retângulos são semelhantes, podem ir direto para o problema; caso contrário, vejam antes a próxima definição.
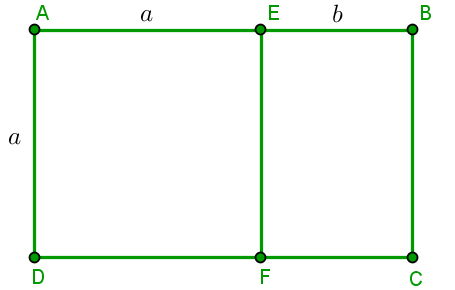
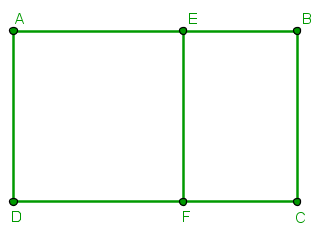 Problema: Considere qualquer retângulo ABCD com a seguinte propriedade:
Problema: Considere qualquer retângulo ABCD com a seguinte propriedade:se dele suprimirmos um quadrado como AEFD, o retângulo restante, EBCF, será semelhante ao retângulo original.
Determinar a razão entre os lados maior e menor do retângulo inicial ABCD.
Apresentamos três dos inúmeros problemas cuja solução consiste em encontrar a raiz positiva da equação [tex]X^2-X-1=0[/tex], portanto já temos uma motivação inicial para darmos um nome especial para o número irracional positivo [tex]\dfrac{1+\sqrt{5}}{2}[/tex]. Vamos lá!

É claro que
- se [tex]\dfrac{b}{a}=\dfrac{a}{a+b}[/tex], então [tex]\dfrac{a}{b}=\dfrac{a+b}{a}[/tex]
e que
- se [tex]\dfrac{a}{b}=\dfrac{a+b}{a}[/tex], então [tex]\dfrac{b}{a}=\dfrac{a}{a+b}[/tex],
logo poderíamos caracterizar a média e extrema razão por qualquer uma das duas igualdades. A opção pela igualdade [tex]\dfrac{b}{a}=\dfrac{a}{a+b}[/tex] foi preservar a definição dada por Euclides, em os Elementos.
Independente de qual seja a igualdade utilizada para definirmos média e extrema razão, a próxima divisão se refere a uma razão específica.

Chamamos de razão áurea a razão entre os comprimentos do maior e do menor segmentos resultantes da divisão do segmento inicial [tex]\overline{AB}[/tex], isto é, [tex]\dfrac{a}{b}[/tex].
Embora possa não parecer, a razão áurea é uma constante que independe do segmento que foi dividido em média e extrema razão. Podemos verificar essa afirmação utilizando parte do raciocínio do segundo problema acima para mostrar que a razão áurea é a raiz positiva da equação [tex]X^2-X-1=0[/tex], qual seja, [tex]\dfrac{1+\sqrt{5}}{2}[/tex].
Finalmente, podemos apresentar formalmente o número de ouro e também outro belo objeto matemático: o retângulo áureo!
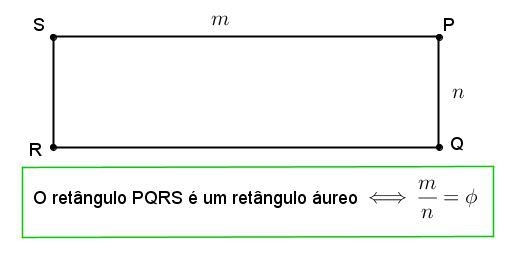
Convém observar que, sendo irracional, o número de ouro é um número decimal infinito e não periódico. Assim, qualquer representação finita de [tex]\Phi[/tex] é uma aproximação e não o valor do número de ouro:
- [tex]\Phi=\dfrac{1+\sqrt{5}}{2}[/tex]
- [tex]\Phi=1,6180339887498948482045868343656381177203091798…[/tex]
- [tex]\Phi\approx1,618[/tex]
III – Como podemos obter a razão áurea?
Resolvam os problemas abaixo e comprovem que a razão áurea aparece, de fato, em várias situações.
1) Determinar um número positivo que seja uma unidade maior do que o seu inverso.
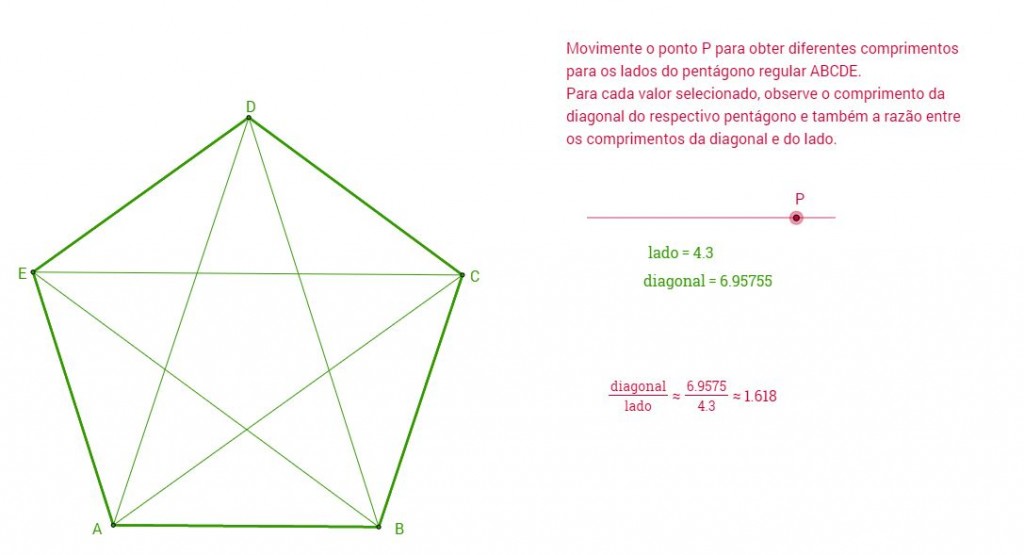
2) Qual o comprimento da diagonal de um pentágono regular cujos lados medem 1?
3) Determinar o valor de[tex]\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+ \, \cdots\textcolor{white}{(}}}}}}}[/tex].
4) Determinar o valor de [tex]1+\dfrac{1}{1+\dfrac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\cdots}}}}}[/tex].
5) Verificar que, se um retângulo de lados com comprimentos [tex]a + b[/tex] e [tex]a[/tex] é áureo, então o retângulo de lados com comprimentos [tex]a[/tex] e [tex]b[/tex] também o é.
IV – Pesquisas
Pesquisem os temas abaixo e, com certeza, vocês encontrarão muita coisa interessante sobre [tex]\Phi[/tex]. Busquem informações na Internet, em livros e não dispensem, mais uma vez, a ajuda imprescindível de seus professores.
1) Mostrem como dividir geometricamente um segmento em média e extrema razão.
2) Mostrem como construir geometricamente um Retângulo Áureo.
3) O que é o “Ângulo de Ouro”?
4) Investiguem uma possível relação do “Ângulo de Ouro” com as sementes e as pétalas de um Girassol.
5) Investiguem se é possível encontrar a Razão Áurea na natureza do crescimento, por exemplo, no crescimento de plantas, em espirais de galáxias, nos dentes dos elefantes e em ondas dos oceanos.
6) Expliquem a relação da Sequência de Fibonacci com a Razão Áurea.
7) Investiguem uma possível relação do Retângulo Áureo com as obras “Mona Lisa” de Leonardo da Vinci e “O Sacramento da Última Ceia” de Salvador Dalí.
8) Investiguem uma possível relação entre a Razão Áurea e o Parthenon / Partenon.
V – Galeria de Vídeos
Aqui vocês encontram vídeos que poderão utilizar nas suas pesquisas.
Cliquem na figura correspondente ao vídeo que vocês querem assistir: na janela que irá abrir, é só clicar na setinha e, depois de assistir ao vídeo escolhido, é só fechar a janela que se abriu.

|
 |
|
Donald no País da Matemágica: Divina proporção |
Os Segredos do Partenon |

|

|
|
Isto é Matemática: A Proporção Divina – Parte 1 |
Isto é Matemática: A Proporção Divina – Parte 2 |

|

|
|
M3 Matemática Multimídia: Um encontro inusitado |
Proporção áurea: ferramenta ou mito? |
|
|
|
Phi Ratio – Sequência de Fibonacci Proporção Áurea |
Matemática em toda parte Artes / Retângulo Áureo |
VI – Pequena Galeria de Arte
Aqui estão duas obras de arte necessárias para suas pesquisas.
 Clique na figura para ampliá-la. |
 Clique na figura para ampliá-la. |
| Obra: O Sacramento da Última Ceia (1955) Autor: Salvador Dalí (1904-1989) Técnica: Óleo sobre tela Estilo: Surrealismo Tamanho: 167 cm × 268 cm Localização: Galeria Nacional de Artes – Washington |
Obra: Mona Lisa (1503–1517) Autor: Leonardo da Vinci (1452-1519) Técnica: Tinta a óleo Estilo: Renascimento Tamanho: 77 cm × 53 cm Localização: Museu do Louvre – Paris |
VII – Galeria de Applets
Disponibilizamos alguns applets para ajudá-los nas investigações propostas. Para facilitar o manuseio e ampliar a área de trabalho, cada applet abrirá em uma outra janela.
Segmento áureo X retângulo áureo
Segmentos áureos e retângulos áureos têm alguma relação?
Com esse applet é possível dividir segmentos quaisquer em média e extrema razão e também construir retângulos áureos a partir do lado menor.
Para utilizar o applet, basta clicar na figura abaixo! 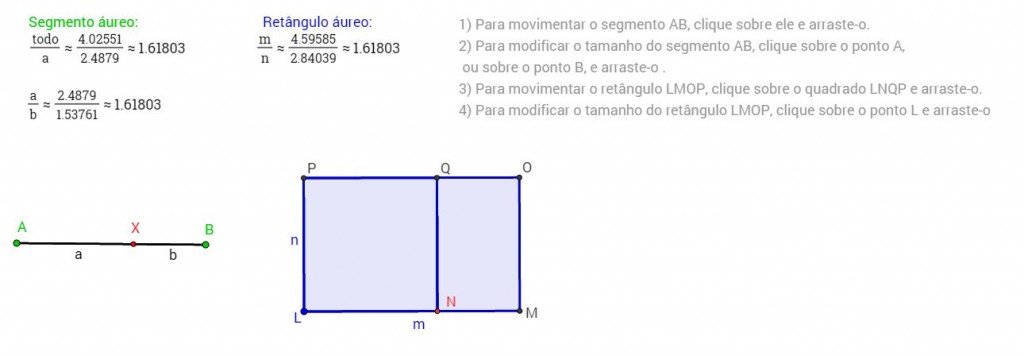
Investigando a Mona Lisa
A proporção áurea está presente na Mona Lisa?
Com este applet é possível procurar por segmentos e retângulos áureos na famosíssima obra de arte Mona Lisa, de Leonardo da Vinci.
Para utilizar o applet, basta clicar na figura abaixo! 
Investigando a Última Ceia
Encontramos a proporção áurea na Última Ceia?
Com este applet também é possível procurar por segmentos e retângulos áureos na obra de arte Última Ceia, de Salvador Dalí.
Para utilizar o applet, basta clicar na figura abaixo! 
VIII – Textos que podem ajudar
Disponibilizamos abaixo links de textos que vocês poderão utilizar nas diversas atividades propostas nas salas sobre a Razão Áurea.
Bom proveito!
❐ A Mitologia e a Verdade da Razão de Ouro (Último acesso em 08/08/18)
❐ Os mitos e verdades sobre a proporção áurea (Último acesso em 08/08/18)
❐ Retângulo áureo e divisão áurea (Último acesso em 08/08/18)
IX – Atividades de Campo
Agora que vocês já estão familiarizados com a razão áurea, que tal utilizarem-na para se divertir?
Escolham um tema, cliquem sobre ele e mãos à obra!
![]() Proporção Áurea: um dos padrões de beleza.
Proporção Áurea: um dos padrões de beleza.
![]() Um concurso de beleza.
Um concurso de beleza.
![]() Procurando a relação áurea …
Procurando a relação áurea …
![]() A Espiral Áurea.
A Espiral Áurea.
➨ Matematicas Visuales (Último acesso em 08/11/19)
➨ O NÚMERO DE OURO E A DIVINA PROPORÇÃO (Último acesso em 08/11/19)
➨ RAZÃO ÁUREA (Último acesso em 08/11/19)
➨ Vídeo: Número de Ouro (Último acesso em 08/11/19)
Equipe COM – OBMEP
Julho de 2015.
➨ Aqua A3 (Último acesso em 08/11/19)
➨ 15 principais obras de Salvador Dali (Último acesso em 08/11/19)
➨ Licenças sob Domínio público via Wikimedia Commons
➨ Wikipedia (Último acesso em 08/11/19)
➨ YouTube (Último acesso em 08/11/19)

Smiles extraídos de Freepik