Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Muito Difícil)
Quantos subconjuntos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] do conjunto [tex]\{m,p,q,t\}[/tex] podemos formar, de modo que:
- [tex]A\cap B\cap C=\emptyset[/tex],
- [tex]A\cap B\ne \emptyset\,\,[/tex] e
- [tex]A\cap C\ne \emptyset [/tex].
AJUDAS
✏ Diagramas de Venn são representações esquemáticas que permitem visualizarmos conjuntos como se fossem regiões do plano. Podemos utilizar esse tipo de representação para organizar os dados de determinados problemas e visualizar melhor um caminho para resolvê-los. A partir de um conjunto universo, os vários conjuntos envolvidos no problema são limitados por figuras fechadas, como círculos, quadrados, retângulos e losangos. O interior de cada figura representa os elementos do respectivo conjunto.
(Se você não se lembra desses diagramas, seria interessante dar uma passadinha nesta Sala de Estudo.)
✏ Combinação simples: Uma das maneiras de agruparmos elementos de um dado conjunto é escolhê-los levando-se em consideração apenas a sua natureza, sem se importar em que ordem eles foram escolhidos ou apresentados. Esse tipo de agrupamento de elementos é denominado uma Combinação simples. Particularmente, quando escolhemos [tex]r[/tex] dentre [tex]n[/tex] elementos de um conjunto dessa forma, dizemos que estamos definindo uma Combinação simples de [tex]n[/tex] elementos tomados [tex]r[/tex] a [tex]r[/tex]. A quantidade desse tipo de agrupamentos é denotada por [tex]C_{n,r}[/tex] ou [tex]C_n^r\,[/tex] e assim definida:
[tex]C_{n,r}=C_n^r=\dfrac{n!}{(n-r)!\,r!} \text{, com } n,r\in\mathbb{N} \text{ e } r\leqslant n[/tex].
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas e
- todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então o número total de maneiras de tomarmos sucessivamente essas [tex]k[/tex] decisões (D1 e D2 e [tex]\cdots[/tex] e Dk) é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
✏ Princípio Aditivo: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas e
- todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então a quantidade de maneiras em que uma das [tex]k[/tex] decisões pode ser tomada (D1 ou D2 ou [tex]\cdots[/tex] ou Dk) é
[tex]\qquad \qquad \boxed{m_1+ m_2 + \cdots + m_k} \, .[/tex]
Solução
Vamos fazer um Diagrama de Venn para ajudar na visualização dos conjuntos que podemos formar. Para isso, observe que:
► [tex]A\cap B\ne \emptyset\,[/tex]. Vamos denotar esse conjunto interseção por [tex]H[/tex]; assim, [tex]\boxed{H=A\cap B}\,.[/tex]
► [tex]A\cap C\ne \emptyset\, [/tex]. Vamos denotar esse conjunto interseção por [tex]G[/tex]; logo, [tex]\boxed{G=A\cap C}\,.[/tex]
► [tex]A\cap B\cap C=\emptyset[/tex]; assim, essa interseção não será representada no nosso diagrama.
► Não temos dados que garantam que [tex]A\cup B\cup C=\{m,\,p,\,q,\,t\}[/tex]; logo, utilizaremos na nossa representação um conjunto universo [tex]U[/tex] para que possamos colocar os possíveis elementos que não estejam em nenhum dos conjuntos [tex]A[/tex], [tex]B[/tex] ou [tex]C\,.[/tex]
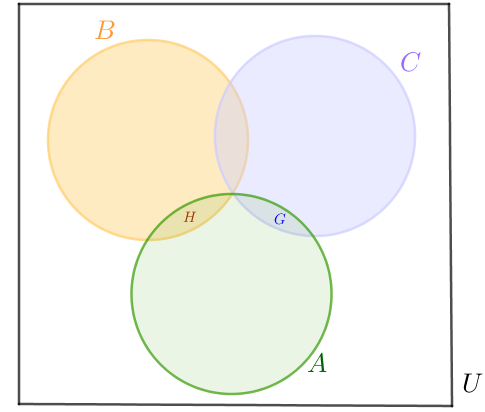Vamos resolver o problema distribuindo os quatro elementos [tex]m,\,p,\,q[/tex] e [tex]t[/tex] nas sete regiões que compõem o diagrama acima:
► elementos apenas de [tex]A[/tex];
► elementos apenas de [tex]B[/tex];
► elementos apenas de [tex]C[/tex];
► elementos apenas de [tex]G[/tex];
► elementos apenas de [tex]H[/tex];
► elementos de [tex]B[/tex] e [tex]C[/tex], mas não de [tex]A[/tex];
► elementos que não são de [tex]A[/tex], nem de [tex]B[/tex] e nem de [tex]C\,.[/tex]
Observe que, como [tex]A\cap B\ne \emptyset\,[/tex] e [tex]A\cap C\ne \emptyset\, [/tex], então devemos colocar pelo menos um elemento em cada região [tex]G[/tex] e [tex]H[/tex]; e esses elementos não podem ser o mesmo, já que [tex]A\cap B\cap C=\emptyset\,.[/tex]
Cada distribuição corresponderá a uma definição de conjuntos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] que satisfazem as condições do problema.
Analisando a quantidade de elementos dos conjuntos [tex]G[/tex] e [tex]H[/tex], temos os seguintes casos possíveis de distribuição:
- Caso 1: [tex]G[/tex] e [tex]H[/tex] têm um elemento cada.
Neste caso, vamos distribuir os quatro elementos [tex]m,\,p,\,q[/tex] e [tex]t[/tex] em quatro etapas: a escolha do elemento de [tex]H[/tex], a escolha do elemento de [tex]G[/tex], a escolha da região na qual o terceiro elemento será colocado e a escolha da região na qual o quarto elemento será colocado.
[tex]\qquad – [/tex] A escolha do elemento de [tex]H[/tex] pode ser feita de [tex]4[/tex] modos distintos.
[tex]\qquad – [/tex] A escolha do elemento de [tex]G[/tex] pode ser feita de [tex]3[/tex] modos distintos.
Os outros dois elementos podem ser colocados em qualquer uma das outras cinco regiões, sem restrições. Portanto:
[tex]\qquad – [/tex] A colocação do terceiro elemento poderá ser feita de [tex]5[/tex] modos distintos.
[tex]\qquad – [/tex] A colocação do quarto elemento poderá ser feita de [tex]5[/tex] modos distintos. - Caso 2: [tex]G[/tex] tem dois elementos e [tex]H[/tex] tem apenas um.
Neste caso, vamos distribuir os quatro elementos [tex]m,\,p,\,q[/tex] e [tex]t[/tex] em três etapas: a escolha dos elementos de [tex]G[/tex], a escolha do elemento de [tex]H[/tex] e a escolha da região na qual o quarto elemento será colocado.
[tex]\qquad – [/tex] A escolha dos dois elementos de [tex]G[/tex] pode ser feita de [tex]C_4^2=\dfrac{4!}{(4-2)!\,2!}=6[/tex] modos distintos.
[tex]\qquad – [/tex] A escolha do elemento de [tex]H[/tex] pode ser feita de [tex]2[/tex] modos distintos.
O último elemento pode ser colocado em qualquer uma das outras cinco regiões, sem restrições. Logo:
[tex]\qquad – [/tex] A colocação do quarto elemento poderá ser feita de [tex]5[/tex] modos distintos. - Caso 3: [tex]H[/tex] tem dois elementos e [tex]G[/tex] tem apenas um.
De maneira análoga ao caso anterior, neste caso, podemos fazer a distribuição dos elementos de
[tex]\qquad \boxed{60}[/tex] maneiras distintas.[tex]\qquad \qquad \textcolor{#800000}{(iii)}[/tex] - Caso 4: [tex]G[/tex] tem três elementos e [tex]H[/tex] tem apenas um.
Neste caso, vamos apenas escolher o elemento de [tex]H[/tex]; os outros três elementos necessariamente serão os elementos de [tex]G.[/tex] Assim, como a escolha do elemento de [tex]H[/tex] pode ser feita de [tex]4[/tex] modos distintos, neste caso podemos fazer a distribuição dos elementos de
[tex]\qquad \boxed{4}[/tex] maneiras distintas. [tex]\qquad \qquad \textcolor{#800000}{(iv)}[/tex] - Caso 5: [tex]H[/tex] tem três elementos e [tex]G[/tex] tem apenas um.
Neste caso, vamos apenas escolher o elemento de [tex]G[/tex]; os outros três elementos necessariamente estarão em [tex]H.[/tex] Como no caso anterior, neste caso podemos fazer a distribuição dos elementos de
[tex]\qquad \boxed{4}[/tex] maneiras distintas. [tex]\qquad \qquad \textcolor{#800000}{(v)}[/tex] - Caso 6: [tex]G[/tex] e [tex]H[/tex] têm dois elementos cada.
Neste caso, vamos distribuir os quatro elementos em duas etapas: a escolha dos elementos de [tex]G[/tex] e a escolha do elemento de [tex]H.[/tex]
[tex]\qquad – [/tex] A escolha dos dois elementos de [tex]G[/tex] pode ser feita de [tex]C_4^2=\dfrac{4!}{(4-2)!\,2!}=6[/tex] modos distintos.
Escolhidos os dois elementos de [tex]G[/tex], os elementos de [tex]H[/tex] ficam automaticamente escolhidos; assim, neste caso, podemos fazer a distribuição dos elementos de
[tex]\qquad \boxed{6}[/tex] maneiras distintas.[tex]\qquad \qquad \textcolor{#800000}{(vi)}[/tex]
Pelo Princípio Multiplicativo, podemos fazer a distribuição dos elementos neste caso de
[tex]\qquad 4 \times 3 \times 5 \times 5=\boxed{300}[/tex] maneiras distintas.[tex]\qquad \qquad \textcolor{#800000}{(i)}[/tex]
Pelo Princípio Multiplicativo, podemos fazer a distribuição dos elementos neste caso de
[tex]\qquad 6 \times 2 \times 5=\boxed{60}[/tex] maneiras distintas. [tex]\qquad \qquad \textcolor{#800000}{(ii)}[/tex]
Dessa forma, por [tex]\textcolor{#800000}{(i)}[/tex], [tex]\textcolor{#800000}{(ii)}[/tex], [tex]\textcolor{#800000}{(iii)}[/tex], [tex]\textcolor{#800000}{(iv)}[/tex], [tex]\textcolor{#800000}{(v)}[/tex], [tex]\textcolor{#800000}{(vi)}[/tex] e pelo Princípio Aditivo, podemos distribuir os elementos [tex]m,\,p,\,q[/tex] e [tex]t[/tex] nas sete regiões que compõem o diagrama que fizemos de
[tex]\qquad 300+60+60+4+4+6=434[/tex] maneiras distintas.
Consequentemente, podemos definir conjuntos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] que atendam às condições do problema de [tex]\fcolorbox{black}{#eee0e5}{$434$}[/tex] maneiras diferentes.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |