Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
Traçamos as diagonais [tex]\overline{AC}\, [/tex] e [tex]\, \overline{BD}[/tex] do trapézio retângulo [tex]ABCD[/tex] mostrado na figura.
A interseção dessas diagonais é o ponto [tex]P[/tex] e as áreas dos triângulos [tex]APD \, [/tex] e [tex]\, ABP [/tex] são [tex]10\, cm^2\, [/tex] e [tex] \, 20\, cm^2[/tex], respectivamente.
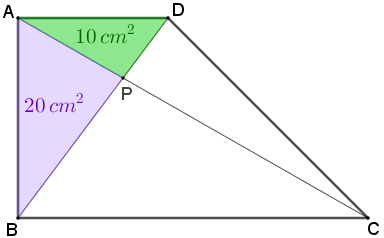
Determinar a área do trapézio [tex]ABCD\, .[/tex]

Lembretes
(1) Se duas retas paralelas são intersectadas por uma transversal, então os pares de ângulos alternos internos que essa transversal define são congruentes. (Precisa relembrar estes conceitos? Dê uma passadinha por aqui.)
(2) Ângulos opostos pelo vértice têm a mesma medida.
(3) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes. (Há uma Sala de Ajuda sobre esse tema no Blog!)
(4) A razão entre as áreas de dois triângulos semelhantes é o quadrado da razão de semelhança.
Solução
Observe que os triângulos [tex]ABD[/tex] e [tex]ACD[/tex] têm a mesma base, com comprimento [tex]b\, [/tex], e a mesma altura, com comprimento [tex]h[/tex]. Assim, esses triângulos têm a mesma área e, consequentemente, a área do triângulo [tex]DPC[/tex] é também [tex]20\, cm^2\, .[/tex]
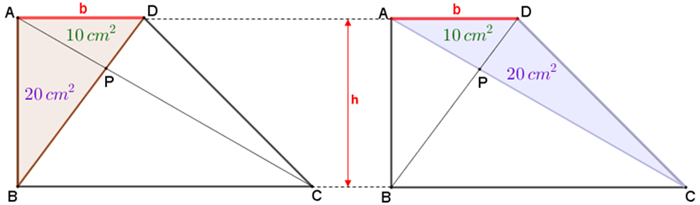
Dessa forma, só precisamos determinar a área do triângulo [tex]BPC[/tex] para calcular a área do trapézio [tex]ABCD\, .[/tex]
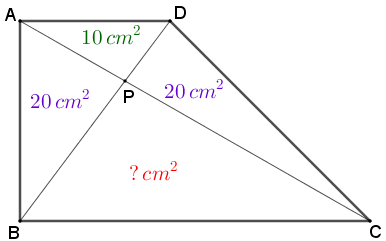
Vamos lá!
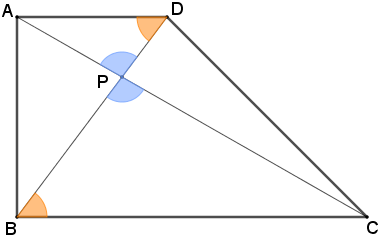
Dessa forma, pelo Lembrete (3), os triângulos [tex]APD[/tex] e [tex]CPB[/tex] são semelhantes.
Segundo o Lembrete (4),
Assim, como conhecemos a área do triângulo [tex]APD[/tex], vamos determinar a razão de semelhança entre os triângulos [tex]APD[/tex] e [tex]BPC.[/tex] E para isso, vamos utilizar o triângulo [tex]ABD[/tex] como intermediário. Observe!
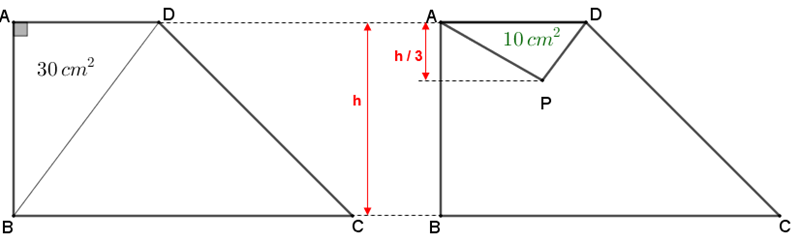
Visto que a altura do triângulo [tex]ABD[/tex] com relação ao lado [tex]\overline{AD}[/tex] é definida pelo segmento [tex]\overline{AB}[/tex], concluímos que a soma das alturas dos triângulos [tex]BPC[/tex] e [tex]APD[/tex] é exatamente a altura [tex]h[/tex] do triângulo [tex]ABD[/tex]. Logo,
► a altura do triângulo [tex]BPC[/tex] é o dobro da altura do triângulo [tex]APD.[/tex]
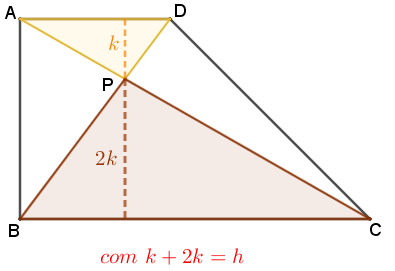
Finalmente, como:
- os triângulos [tex]APD[/tex] e [tex]BPC[/tex] são semelhantes, com razão de semelhança [tex]2[/tex] e
- a área do triângulo [tex]APD[/tex] é [tex]10\, cm^2[/tex],
então, o Lembrete (4) nos garante que a área do triângulo [tex]BPC[/tex] é [tex]\, \fcolorbox{black}{#d7d7d7}{$2^2 \times 10=40\, cm^2$}\, .[/tex]
Portanto, a área do trapézio [tex]ABCD\, [/tex] é [tex]\, \fcolorbox{black}{#eee0e5}{$20+10+20+40=90\, cm^2$}\, .[/tex]
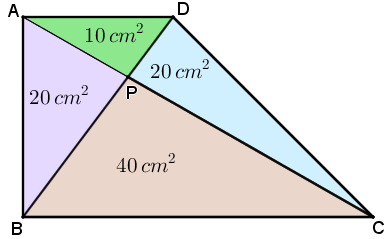
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
