(A) Problema para ajudar na escola: Dois retângulos

Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)

No interior de um retângulo [tex]EFGH [/tex] cuja área é [tex]2.018 \, cm^2 \, [/tex], traçamos uma circunferência de centro em [tex]O \, [/tex] e inscrita no triângulo [tex]EFG[/tex], conforme mostra a figura abaixo.

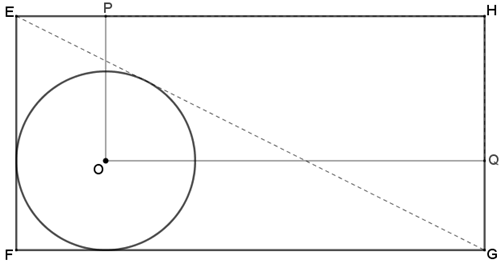
Sabendo que os segmentos [tex]\overline{OP} \, [/tex] e [tex] \, \overline{OQ} \, [/tex] são paralelos aos lados do retângulo [tex]EFGH[/tex], determine a área do retângulo [tex]POQH.[/tex]

Solução

Sejam

• [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] os pontos de tangência da circunferência e do triângulo [tex]EFG[/tex];
• [tex]R[/tex] o ponto de interseção dos segmentos [tex]\overline{EG}[/tex] e [tex]\overline{OQ}[/tex];
• [tex]S[/tex] o ponto de interseção dos segmentos [tex]\overline{PO}[/tex] e [tex]\overline{EG}[/tex];
• [tex]r[/tex] o comprimento do raio da circunferência;

conforme indicados na figura a seguir. Aproveite a figura e observe os vários segmentos com comprimento [tex]r[/tex]: todos serão uteis na nossa resolução.

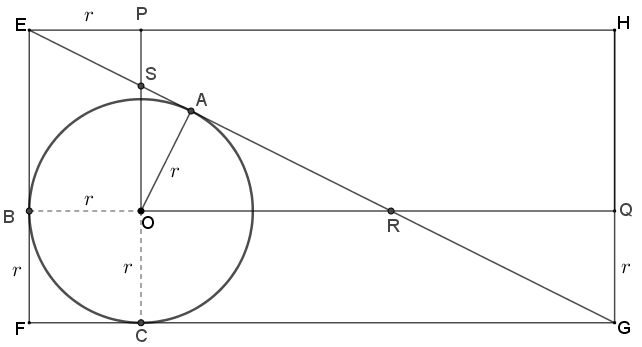
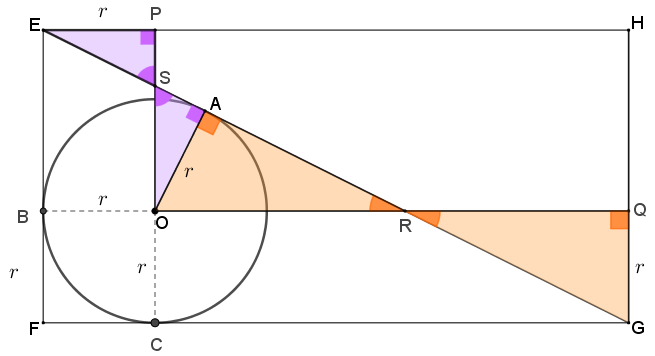
Analisemos dois pares de triângulos:

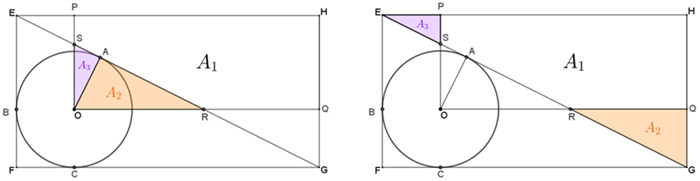
Seja [tex]A_{POQH}[/tex] a área do retângulo [tex]POQH.[/tex] A figura abaixo à esquerda nos mostra que [tex]A_{POQH}=A_1+A_2+A_3.[/tex]
Mas os triângulos [tex]EPS \, [/tex] e [tex] \, OAS[/tex] são congruentes, assim como [tex]OAR \, [/tex] e [tex] \, GQR[/tex]; portanto, pelo Lembrete (3), a área do retângulo [tex]POQH[/tex] é igual à área do triângulo retângulo [tex] EHG[/tex], que, por sua vez, é a metade da área do retângulo [tex]EFGH.[/tex]

Assim:
[tex]\qquad A_{POQH}=\dfrac{2018}{2}=1009[/tex]
e, portanto, a área do retângulo [tex]POQH[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$1.009 \, cm^2$} \, \, .[/tex]

Solução elaborada pelos Moderadores do Blog.