Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
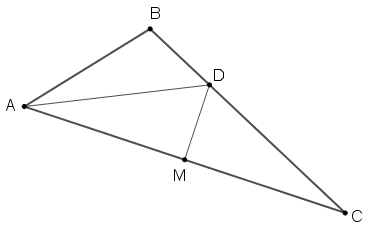
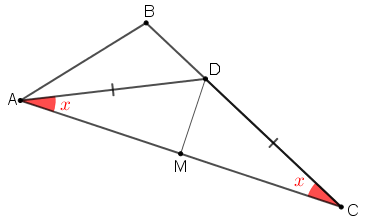
Na figura, [tex]ABC[/tex] é um triângulo, [tex]D[/tex] é um ponto no lado [tex]\overline{BC}[/tex] e [tex] \, M \, [/tex] é um ponto no lado [tex]\overline{AC}[/tex].
Sabe-se que o segmento [tex]\overline{AD}[/tex] é a bissetriz do ângulo [tex]\angle BAC[/tex] e que [tex]D[/tex] e [tex]M[/tex] são pontos da mediatriz do lado [tex]\overline{AC}.[/tex]
Se a medida do ângulo [tex]\angle ABC[/tex] é [tex]105^\circ[/tex], qual a medida em graus do ângulo [tex]\angle BCA[/tex]?

Lembrete
Quando na matemática falamos que dois triângulos são "geometricamente iguais" queremos dizer que:
- as medidas dos lados de um triângulo são ordenadamente iguais às medidas dos lados do outro e
- as medidas dos ângulos de um triângulo são ordenadamente iguais à medidas dos ângulos do outro.
Essa “igualdade geométrica” é o que conhecemos como congruência. Assim, informalmente, dois triângulos são congruentes se for possível movimentar um deles, sem deformá-lo, até fazê-lo coincidir com o outro, podendo para isso até sair do plano no qual ele foi desenhado.
Para verificarmos se dois triângulos são congruentes não é necessário comparar as três medidas dos lados e as três medidas dos ângulos de um desses triângulos como as respectivas medidas do outro. Existem condições nas quais apenas três comparações de medidas são suficientes para se concluir que dois triângulos são congruentes. Essas condições mínimas são chamadas de critérios de congruência. (Nesses casos, as demais igualdades são consequências dessas três condições mínimas e podem ser obtidas a partir destas por meio de argumentações teóricas apropriadas que fogem ao objetivo deste texto.).
Para resolver este problema precisaremos de um dos critérios de congruência entre triângulos: o caso L.A.L., que apresentamos abaixo.
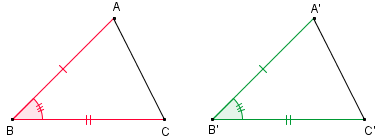
Caso de congruência L.A.L. (lado, ângulo, lado)
Dois triângulos são congruentes se “dois lados de um triângulo e o ângulo definido por esses lados” têm, respectivamente, as mesmas medidas de “dois lados do outro triângulo e o ângulo determinado por estes”.
(Se for conveniente, dê uma passadinha nesta Sala, mais tarde!)
Solução 1
Seja [tex]x[/tex] a medida em graus do ângulo [tex]\angle BCA.[/tex]
Observe que como [tex]D[/tex] e [tex]M[/tex] são pontos da mediatriz do lado [tex]\overline{AC}[/tex], então
- os ângulos [tex]\angle DMC \, [/tex] e [tex]\angle DMA \, [/tex] são ângulos retos, logo têm a mesma medida;
- os segmentos [tex]\overline{AM}[/tex] e [tex]\overline{MC}[/tex] têm a mesma medida.
Observe também que
- o segmento [tex]\overline{DM}[/tex] é um lado comum aos triângulos [tex]DMC[/tex] e [tex]DMA[/tex].
Dessa forma, pelo caso de congruência L.A.L., os triângulos [tex]DMC[/tex] e [tex]DMA[/tex] são congruentes e, assim, particularmente os ângulos [tex]\angle DCA \, [/tex] e [tex]\angle DAC \, [/tex] têm a mesma medida. Então, a medida em graus de [tex]\angle DAC \, [/tex] é [tex] \, x[/tex].
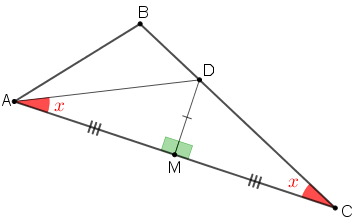
Note agora que, como [tex]\overline{AD}[/tex] é a bissetriz do ângulo [tex]\angle BAC \, [/tex], então os ângulos [tex]\angle BAD \, [/tex] e [tex]\angle DAC \, [/tex] têm a mesma medida e com isso a medida em graus de [tex]\angle BAD \, [/tex] é também [tex]x[/tex].
Por outro lado, sabemos que a medida do ângulo [tex]∠ABC[/tex] é [tex]105^\circ[/tex] e que a soma das medidas em graus dos ângulos internos de um triângulo é [tex]180^\circ[/tex]. Assim, com relação ao triângulo [tex]ABC \, [/tex], podemos afirmar que [tex]105^\circ +2x+x=180^\circ[/tex].
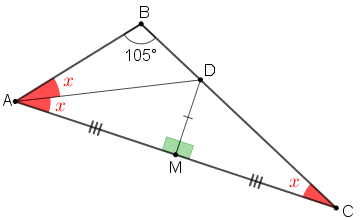
Dessa forma, segue que:
[tex]\qquad 105^\circ +3x=180^\circ[/tex]
[tex]\qquad 3x=180^\circ-105^\circ[/tex]
[tex]\qquad 3x=75^\circ[/tex]
[tex]\qquad x=25^\circ.[/tex]
Portanto, a medida do ângulo [tex]\angle BCA[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$25^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.

Ajuda para a segunda solução
Para a próxima solução, precisaremos de uma propriedade importante sobre mediatriz de um segmento:
Os pontos da mediatriz de um segmento equidistam de suas extremidades.
ou, de outra forma:
Se [tex]P[/tex] é um ponto qualquer da mediatriz de um segmento [tex]\overline{RS}[/tex], então as distâncias de [tex]P[/tex] a [tex]R[/tex] e de [tex]P[/tex] a [tex]S[/tex] são iguais.
(Se você não conhece essa propriedade, dê uma passadinha nesta Sala, mais tarde!)
Solução 2
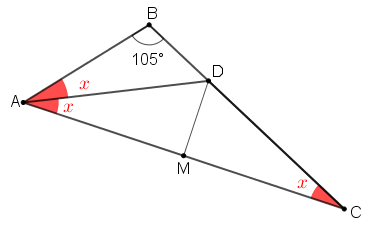
Seja [tex]x[/tex] a medida em graus do ângulo [tex]\angle BCA [/tex] e observe que os ângulos [tex]\angle BCA[/tex] e [tex]\angle DCA[/tex] são iguais.
Por outro lado, como [tex]D[/tex] é um ponto da mediatriz do lado [tex]\overline{AC}[/tex], então as distâncias de [tex]D[/tex] a [tex]A[/tex] e de [tex]D[/tex] a [tex]C[/tex] são iguais.
Dessa forma, o triângulo [tex]DAC[/tex] é isósceles e, consequentemente, os ângulos [tex]\angle DCA \, [/tex] e [tex]\angle DAC \, [/tex] têm a mesma medida [tex] \, x[/tex].
Note agora que, como [tex]\overline{AD}[/tex] é a bissetriz do ângulo [tex]\angle BAC \, [/tex], então os ângulos [tex]\angle BAD \, [/tex] e [tex]\angle DAC \, [/tex] têm a mesma medida e com isso a medida em graus de [tex]\angle BAD \, [/tex] é também [tex]x[/tex].
Lembre, também, que a medida do ângulo [tex]\angle ABC[/tex] é [tex]105^\circ[/tex]; assim, como a soma das medidas em graus dos ângulos internos de um triângulo é [tex]180^\circ \, [/tex], temos que [tex]105^\circ +2x+x=180^\circ[/tex].
Dessa forma, segue que:
[tex]\qquad 105^\circ +3x=180^\circ[/tex]
[tex]\qquad 3x=180^\circ-105^\circ[/tex]
[tex]\qquad 3x=75^\circ[/tex]
[tex]\qquad x=25^\circ.[/tex]
Portanto, a medida do ângulo [tex]\angle BCA[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$25^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Nível B – Questão Média
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
