Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
(PUCRJ-2014-adaptado) Considere o triângulo equilátero [tex]ABC[/tex] inscrito no círculo de raio [tex]1[/tex] e centro [tex]O[/tex], como apresentado na figura abaixo.
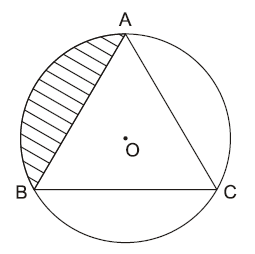
(a) Calcule a medida do ângulo [tex]A\hat{O}B[/tex] em graus e em radianos.
(b) Calcule a área da região hachurada.
Lembretes
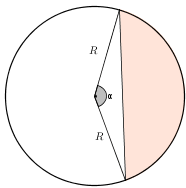
✐ (1) Área de um segmento circular de raio [tex]R[/tex] e [tex]\alpha[/tex] radianos:
[tex]\qquad \qquad \boxed{A_{segm}=\dfrac{R^{ \, 2}}{2}\left(\alpha-sen \, \alpha\right)}[/tex]
(Para aprender um pouco mais sobre segmento circular, clique AQUI.)
✐ (2) Área de um triangulo equilátero inscrito em uma circunferência de raio [tex]R[/tex]:
[tex]\qquad \qquad \boxed{A_{teq}=\dfrac{3 \cdot R^{ \, 2} \cdot \sqrt{3}}{4}}[/tex]
(Se você não conhece essa fórmula, clique AQUI.)
✐ (3) A um arco de circunferência podemos associar duas medidas distintas:
– a sua medida angular;
– a sua medida linear.
Ambas podem ser obtidas a partir do " comprimento e da medida angular da circunferência que define o arco".
(Se você não se lembra dessas medidas, clique AQUI.)
Solução
Seja [tex]\lambda[/tex] a circunferência de centro em [tex]O[/tex] e raio [tex]1[/tex] na qual o triângulo [tex]ABC[/tex] está inscrito.
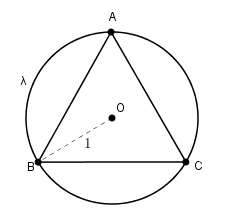
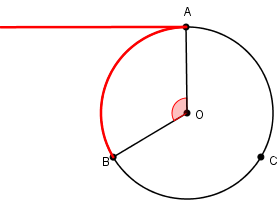
(a) O ângulo [tex]A\hat{O}B[/tex] é um ângulo central relativo à circunferência [tex]\lambda[/tex], assim ele determina um arco sobre [tex]\lambda[/tex]: [tex]\stackrel{\frown}{AB}[/tex].
Pelo Lembrete (3), ao arco [tex]\stackrel{\frown}{AB}[/tex] podemos associar duas medidas: a sua medida angular e a sua medida linear. Dessa forma, podemos associar ao ângulo [tex]A\hat{O}B[/tex] duas medidas:
- a medida em graus de [tex]A\hat{O}B[/tex] é exatamente a medida angular do arco que ele determina sobre [tex]\lambda[/tex];
- a medida em radianos de [tex]A\hat{O}B[/tex] é o valor numérico da medida linear (o comprimento) do arco que ele determina sobre [tex]\lambda[/tex], já que o raio de [tex] \lambda[/tex] é [tex]1[/tex].
Vamos, então, calcular a medida angular e o comprimento do arco [tex]\stackrel{\frown}{AB}[/tex] para determinarmos a medida em graus e em radianos do ângulo [tex]A\hat{O}B[/tex]. Para isso, o nosso ponto de partida será a seguinte observação:
- Como o triângulo [tex]ABC[/tex] é equilátero, os vértices [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] dividem a circunferência [tex]\lambda[/tex] em três arcos congruentes. Assim, [tex]\stackrel{\frown}{AB}[/tex], [tex]\stackrel{\frown}{BC}[/tex] e [tex]\stackrel{\frown}{CA}[/tex] são arcos com o mesmo comprimento: [tex]\dfrac{1}{3}[/tex] do comprimento de [tex]\lambda[/tex].
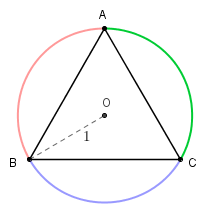
[tex]\textcolor{#800000}{(i)}[/tex] Uma circunferência tem medida angular [tex]360^\circ[/tex], consequentemente, a medida angular de [tex]\stackrel{\frown}{AB}[/tex] é [tex]\dfrac{360^\circ}{3}[/tex], ou seja, [tex]120^\circ[/tex].
Pelo exposto, concluímos que a medida, em graus, do ângulo [tex]A\hat{O}B[/tex] será também [tex]\fcolorbox{black}{#eee0e5}{$120^\circ$}[/tex].
[tex]\textcolor{#800000}{(ii)}[/tex] Como o comprimento de uma circunferência de raio [tex]1[/tex] é [tex]2\pi[/tex] e os arcos [tex]\stackrel{\frown}{AB}[/tex], [tex]\stackrel{\frown}{BC}[/tex] e [tex]\stackrel{\frown}{CA}[/tex] são congruentes, então o comprimento de [tex]\stackrel{\frown}{AB}[/tex] é [tex]\dfrac{2\pi}{3}[/tex].
Poderíamos também ter obtido o comprimento [tex]c[/tex] do arco [tex]\stackrel{\frown}{AB}[/tex], a partir de sua medida em graus, utilizando a regra de três abaixo indicada:
| [tex]2\pi [/tex] | ————————————– | [tex]360^\circ[/tex] |
| [tex]c[/tex] | ————————————– | [tex]120^\circ[/tex] |
De qualquer modo, [tex]A\hat{O}B[/tex] mede [tex]\fcolorbox{black}{#eee0e5}{$\dfrac{2\pi}{3} \, radianos$}[/tex].
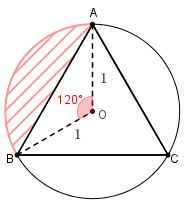(b) Seja [tex]A[/tex] a área que devemos calcular neste item. Vamos calculá-la de duas maneiras.
[tex]\textcolor{#800000}{(i)}[/tex] Observe que [tex]A[/tex] pode ser considerada a área de um segmento circular de raio [tex]1[/tex] e [tex]\dfrac{2\pi}{3}[/tex] radianos.
Assim, pelo Lembrete (1) segue que:
[tex]\quad A=\dfrac{1^{ \, 2}}{2}\left(\dfrac{2\pi}{3}-sen \, \dfrac{2\pi}{3}\right)[/tex]
[tex]\quad A=\dfrac{1}{2}\left(\dfrac{2\pi}{3}-\dfrac{\sqrt{3}}{2}\right)[/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$A=\dfrac{4\pi-3\sqrt{3}}{12}$}[/tex] unidades de área.
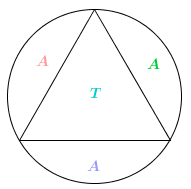
[tex]\textcolor{#800000}{(ii)}[/tex] Como [tex]\stackrel{\frown}{AB}[/tex], [tex]\stackrel{\frown}{BC}[/tex] e [tex]\stackrel{\frown}{CA}[/tex] são arcos com o mesmo comprimento, [tex]A[/tex] corresponde a [tex]\dfrac{1}{3}[/tex] da área do círculo menos a área da região definida pelo triângulo [tex]ABC[/tex].
Como a área do círculo é [tex]\pi (1)^2=\pi[/tex], se [tex]T[/tex] for a área triangular [tex]ABC[/tex], então [tex]\boxed{A=\dfrac{1}{3}\left(\pi-T\right)}[/tex]. Portanto, basta calcularmos [tex]T[/tex].
Pelo Lembrete (2), segue que:
[tex]\quad T=\dfrac{3 \cdot 1^{ \, 2} \cdot \sqrt{3}}{4}[/tex]
[tex]\quad T=\dfrac{3 \sqrt{3}}{4}[/tex],
assim,
[tex]\quad A=\dfrac{1}{3}\left(\pi-\dfrac{3 \sqrt{3}}{4}\right)=\dfrac{1}{3}\left(\dfrac{4 \pi-3 \sqrt{3}}{4}\right)[/tex]
ou seja, [tex]\fcolorbox{black}{#eee0e5}{$A=\dfrac{4\pi-3\sqrt{3}}{12}$}[/tex] unidades de área.
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |