✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M.- Nível de dificuldade: Difícil)
(UNICAMP, 2004) Considere o conjunto dos dígitos [tex]\{1, 2, 3, …, 9\}[/tex] e forme com eles números de nove algarismos distintos.
(a) Quantos desses números serão pares?
(b) Escolhendo-se ao acaso um dos números do item (a), qual a probabilidade de que este número tenha exatamente dois dígitos ímpares juntos?

Lembrete
✐ Princípio Fundamental da Contagem, ou Princípio Multiplicativo, para [tex]k [/tex] eventos: Se
- um evento E1 puder ocorrer de [tex] m_1 [/tex] maneiras,
- um evento E2 puder ocorrer de [tex]m_2 [/tex] maneiras,
- [tex]\cdots[/tex]
- um evento Ek puder ocorrer de [tex]m_k [/tex] maneiras
e todos esses eventos forem independentes entre si (isto é, a ocorrência de um não muda a quantidade de possibilidades para a ocorrência de outro), então a quantidade de maneiras em que os [tex]k[/tex] eventos ocorrem ao mesmo tempo é
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
(a) Observe que os números pares que podemos formar com os algarismos [tex]1, 2, 3, …, 9[/tex] são aqueles que terminam em [tex]2,4, 6[/tex] ou [tex]8[/tex]. Dessa forma, vamos dividir a nossa contagem de números pares de nove algarismos distintos que podemos formar com algarismos [tex]1, 2, 3, …, 9[/tex] em dois eventos: a escolha do último dígito e a escolha dos outros oito dígitos. Utilizando a notação do Lembrete, calcularemos [tex]m_1[/tex] e [tex]m_2[/tex] e a resposta deste item será o produto [tex]m_1 \times m_2[/tex].
- Evento 1: Escolha do último dígito
- Evento 2: Escolha dos demais dígitos
Podemos escolher o último dígito de [tex]4[/tex] maneiras diferentes: ou [tex]2[/tex] ou [tex]4[/tex] ou [tex]6[/tex] ou [tex]8[/tex].
Logo, [tex]\boxed{m_1=4}[/tex].
Vamos dividir este evento em oito etapas independentes entre si: escolha do primeiro dígito, escolha do segundo dígito, …, escolha do oitavo dígito; e aplicar o Princípio Fundamental da Contagem para calcular a quantidade de maneiras em que esses oito eventos ocorrem ao mesmo tempo obtendo, então, [tex]m_2[/tex].
Observe que, dos nove algarismos disponíveis, restam oito, já que utilizamos um deles como último dígito. Podemos então escolher o primeiro dígito de [tex]8[/tex] maneiras diferentes; o segundo, de [tex]7[/tex] maneiras; o terceiro de [tex]6[/tex] e assim sucessivamente até o oitavo dígito.
O esqueminha abaixo ajuda na visualização da contagem.
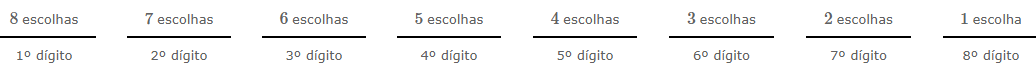
Logo, pelo Princípio Fundamental da Contagem, segue que:
[tex]\qquad m_2=8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 =8![/tex],
ou seja, [tex]\boxed{m_2=40\,320}[/tex].
Portanto, podemos formar [tex] 4 \times 40\,320 =\, \fcolorbox{black}{#eee0e5}{$\, 161\,280$}\,[/tex] números pares com nove algarismos distintos utilizando o conjunto dos dígitos [tex]\{1, 2, 3, …, 9\}[/tex].
Observação: Se você sabe o que é uma Permutação, você poderia ter obtido o valor de [tex]m_2[/tex] rapidamente, já que a escolha dos oito primeiros dígitos dos números pares que queremos contar é, simplesmente, o número de permutações de oito objetos distintos, isto é, [tex]m_2=8![/tex].
Dessa forma, igualmente, o resultado final seria [tex]m_1 \times m_2=4 \times 8!= 161\,280[/tex].
(b) A escolha de dígitos do conjunto [tex]\{1, 2, 3, …, 9\}[/tex] para se formar com eles números pares de nove algarismos distintos é um experimento aleatório cujo espaço amostral, embora com muitos elementos, é finito e equiprovável. Assim, escolhendo-se ao acaso um dos números do item (a), a probabilidade [tex]P[/tex] de que este número tenha exatamente dois dígitos ímpares juntos é dada pela razão entre "casos favoráveis" e " casos possíveis ", ou seja:

Para que um número par com nove dígitos distintos e todos os nove diferentes de [tex]0[/tex] tenha exatamente dois algarismos ímpares em posições consecutivas, esse número deve ter uma das seguintes formas:
[tex]\qquad \qquad \boxed{\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{red}{i}\textcolor{blue}{p}} \quad ; \quad \boxed{\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}} \quad ; \quad \boxed{\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}} \quad ; \quad \boxed{\textcolor{red}{i}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}}.[/tex]
Vamos fazer a contagem do total de números com essas quatro formas separadamente.
- Forma [tex]\boxed{\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{red}{i}\textcolor{blue}{p}}[/tex]:
- os algarismos ímpares poderão ser escolhidos de [tex]5\times 4 \times 3 \times 2 \times 1=5![/tex] modos distintos;
- os algarismos pares poderão ser escolhidos de [tex]4 \times 3 \times 2 \times 1=4![/tex] modos distintos;
Temos cinco algarismos ímpares para ocuparem cinco posições e quatro algarismos pares para ocuparem quatro posições:
| [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | |||||||||
| [tex]5[/tex] alg. | [tex]4[/tex] alg. | [tex]4[/tex] alg. | [tex]3[/tex] alg. | [tex]3[/tex] alg. | [tex]2[/tex] alg. | [tex]2[/tex] alg. | [tex]1[/tex] alg. | [tex]1[/tex] alg. |
Assim, pelo Princípio Fundamental da Contagem
e, portanto, temos [tex]\boxed{5! \times 4!}[/tex] modos de formar esses tipos de números.
As próximas contagens serão idênticas a esta que acabamos de fazer, mas vamos explicitá-las para um melhor entendimento!
- Forma [tex]\boxed{\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}}[/tex]:
Temos cinco algarismos ímpares para ocuparem cinco posições e quatro algarismos pares para ocuparem quatro posições:
| [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | |||||||||
| [tex]5[/tex] alg. | [tex]4[/tex] alg. | [tex]4[/tex] alg. | [tex]3[/tex] alg. | [tex]3[/tex] alg. | [tex]2[/tex] alg. | [tex]2[/tex] alg. | [tex]1[/tex] alg. | [tex]1[/tex] alg. |
Assim, pelo Princípio Fundamental da Contagem temos [tex]\boxed{5! \times 4!}[/tex] modos de formar esse tipo de números.
- Forma [tex]\boxed{\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}}[/tex]:
Temos cinco algarismos ímpares para ocuparem cinco posições e quatro algarismos pares para ocuparem quatro posições:
| [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | |||||||||
| [tex]5[/tex] alg. | [tex]4[/tex] alg. | [tex]4[/tex] alg. | [tex]3[/tex] alg. | [tex]3[/tex] alg. | [tex]2[/tex] alg. | [tex]2[/tex] alg. | [tex]1[/tex] alg. | [tex]1[/tex] alg. |
Novamente, pelo Princípio Fundamental da Contagem temos [tex]\boxed{5! \times 4!}[/tex] modos de formar esse tipo de números.
- Forma [tex]\boxed{\textcolor{red}{i}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}\textcolor{red}{i}\textcolor{blue}{p}}[/tex]:
Temos cinco algarismos ímpares para ocuparem cinco posições e quatro algarismos pares para ocuparem quatro posições:
| [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | [tex]\textcolor{red}{i}[/tex] | [tex]\textcolor{blue}{p}[/tex] | |||||||||
| [tex]5[/tex] alg. | [tex]4[/tex] alg. | [tex]4[/tex] alg. | [tex]3[/tex] alg. | [tex]3[/tex] alg. | [tex]2[/tex] alg. | [tex]2[/tex] alg. | [tex]1[/tex] alg. | [tex]1[/tex] alg. |
Também pelo Princípio Fundamental da Contagem temos [tex]\boxed{5! \times 4!}[/tex] modos de formar esse tipo de números.
Dessa forma, temos um total de [tex]\boxed{4 \times 5! \times 4!}[/tex] números pares com nove dígitos distintos, todos os nove diferentes de zero, que tenham exatamente dois algarismos ímpares em posições consecutivas.
Aqui, também observamos que se você sabe o que é uma Permutação, você poderia ter feito essa contagem observando que a quantidade das escolhas dos algarismos ímpares corresponde ao número de permutações de cinco objetos distintos ([tex]5![/tex]) e a quantidade das escolhas dos algarismos pares corresponde ao número de permutações de quatro objetos distintos ([tex]4![/tex])
Finalmente, a probabilidade [tex]P[/tex] de que escolhido ao acaso um dos números do item (a) este número tenha exatamente dois dígitos ímpares juntos é dada por:
[tex]\qquad \qquad P=\dfrac{4 \times 5! \times 4!}{161280}=\dfrac{11520}{161280}=\dfrac{1}{14}\approx 0,071.[/tex]
Portanto, [tex] \, \fcolorbox{black}{#eee0e5}{$\, P \approx 7,1\%$}\,[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
