.Problema para ajudar na escola: O raio da circunferência inscrita

Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)

• os lados [tex]AB\,[/tex] e [tex]\,AC\,[/tex] têm o mesmo comprimento;
• o lado [tex]BC[/tex] mede [tex]4n\,[/tex] centímetros;
• a altura relativa ao lado [tex]BC[/tex] mede [tex]\left(n^2-1\right)[/tex] centímetros.

Determinar todos os valores de [tex]n[/tex] para os quais a medida em centímetros do raio da circunferência inscrita no triângulo [tex]ABC[/tex] seja um número inteiro.

Solução 1

Vamos fazer duas figuras com os dados do problema, para facilitar a nossa solução.

• Na figura da esquerda, já vamos inserir algumas conclusões que obtemos utilizando os dois primeiros Lembretes:
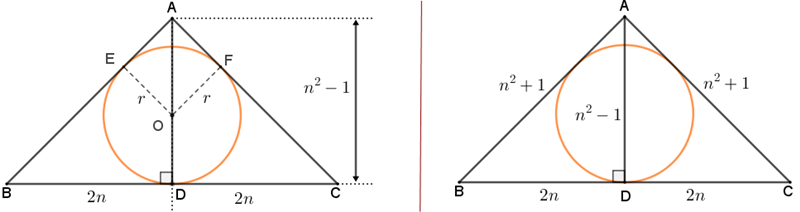
  como o ponto [tex]O[/tex] é o centro da circunferência inscrita no triângulo [tex]ABC[/tex], a semirreta [tex]AO[/tex] é uma bissetriz e, portanto, o segmento [tex]\overline{AD}[/tex] é também a mediana e a altura desse triângulo relativa à base [tex]\overline{BC}.[/tex] Dessa forma, o comprimento em centímetros dos segmentos [tex]\overline{BD}[/tex] e [tex]\overline{DC}[/tex] é [tex]2n.[/tex]
  Vamos considerar que [tex]E[/tex] e [tex]F[/tex] são pontos de tangência da circunferência inscrita e que [tex]r[/tex] é o comprimento do raio dessa circunferência.
• Note que, como os triângulos [tex]ABD[/tex] e [tex]ACD[/tex] são retângulos, o Teorema de Pitágoras nos permite obter os comprimentos dos lados [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex]:

[tex]\qquad AB^2=(2n)^2+\left(n^2-1\right)^2[/tex]
[tex]\qquad AB^2=4n^2+n^4-2n^2+1[/tex]
[tex]\qquad AB^2=4n^2+n^4-2n^2+1[/tex]
[tex]\qquad AB^2=n^4+2n^2+1[/tex]
[tex]\qquad AB^2=\left(n^2+1\right)^2[/tex]
[tex]\qquad \boxed{AB=n^2+1}[/tex].

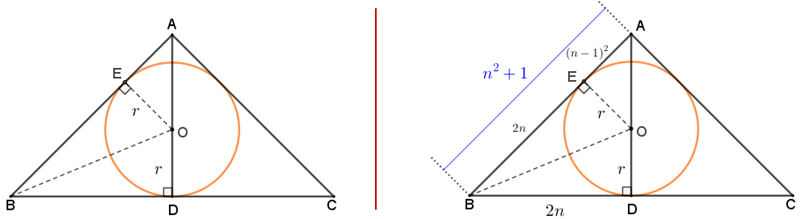
• Observe agora que, utilizando o caso de congruência citado nos Lembretes, podemos concluir que os triângulos [tex]OEB[/tex] e [tex]ODB[/tex] são congruentes.

Assim, [tex]EB=DB=2n[/tex] e, portanto, segue que:
[tex]\qquad AE=AB-EB[/tex]
[tex]\qquad AE=\left(n^2+1\right)-2n[/tex]
[tex]\qquad AE=n^2-2n+1[/tex]
[tex]\qquad \boxed{AE=\left(n-1\right)^2}.[/tex]

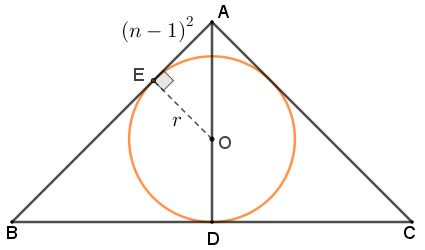
• Aplicando uma vez mais o Teorema de Pitágoras, agora ao triângulo retângulo [tex]AEO[/tex], temos que:

[tex]\qquad AO^2=EO^2+AE^2[/tex]
[tex]\qquad AO^2=r^2+\left(\left(n-1\right)^2\right)^2[/tex]
[tex]\qquad AO=\sqrt{r^2+\left(n^2-1\right)^4}.[/tex]

• Como [tex]AD=AO+OD[/tex], segue que:

[tex]\qquad n^2-1=\sqrt{r^2+\left(n-1\right)^4}+r[/tex]
[tex]\qquad \sqrt{r^2+\left(n-1\right)^4}=n^2-1-r[/tex]
[tex]\qquad \left(\sqrt{r^2+\left(n-1\right)^4}\right)^2=\left(n^2-1-r\right)^2[/tex]
[tex]\qquad r^2+\left(n-1\right)^4=\left(n^2-1-r\right)^2[/tex]
[tex]\qquad r^2+n^4-4n^3+6n^2-4n+1=n^4-2n^2-2rn^2+2r+1+r^2[/tex]
[tex]\qquad \cancel{r^2}+\bcancel{n^4}-4n^3+6n^2-4n+\xcancel{1}=\bcancel{n^4}-2n^2-2rn^2+2r+\xcancel{1}+\cancel{r^2}[/tex]
[tex]\qquad -4n^3+6n^2-4n=-2n^2-2rn^2+2r[/tex]
[tex]\qquad -4n^3+8n^2-4n=-2rn^2+2r[/tex]
[tex]\qquad rn^2-r=2n^3-4n^2+2n[/tex]
[tex]\qquad r\left(n^2-1\right)=2n\left(n^2-2n+1\right)[/tex]
[tex]\qquad r\left(n+1\right)\left(n-1\right)=2n\left(n-1\right)^2[/tex]
[tex]\qquad r\left(n+1\right)\bcancel{\left(n-1\right)}=2n\left(n-1\right)\bcancel{\left(n-1\right)}[/tex]
[tex]\qquad r\left(n+1\right)=2n\left(n-1\right)[/tex]
[tex]\qquad r=2n\cdot\dfrac{n-1}{n+1}.\qquad \qquad \textcolor{#800000}{(i)}[/tex]

Queremos que o comprimento [tex]r[/tex] do raio da circunferência seja um número natural; assim, vamos tentar reescrever [tex]\textcolor{#800000}{(i)}[/tex] explicitando números inteiros do lado direito da igualdade:
[tex]\qquad r=2n\cdot\dfrac{n-1}{n+1}\\
\qquad r=2n\cdot\dfrac{n+1-2}{n+1}=2n\cdot\left(\dfrac{n+1}{n+1}-\dfrac{2}{n+1}\right)\\
\qquad r=2n\cdot\left(1-\dfrac{2}{n+1}\right)=2n-\dfrac{4n}{n+1}\\
\qquad r=2n-\dfrac{4n+4-4}{n+1}\\
\qquad r=2n-\dfrac{4n+4}{n+1}+\dfrac{4}{n+1}=2n-\dfrac{4\cdot (n+1)}{n+1}+\dfrac{4}{n+1}\\
\qquad r=2n-4+\dfrac{4}{n+1}.[/tex]
Perceba que [tex]2n-4[/tex] é um número inteiro; assim, para que [tex]r[/tex] seja de fato um inteiro positivo, necessariamente [tex]\dfrac{4}{n+1}[/tex] deve ser um número natural.
Dessa forma, a princípio, temos apenas três opções: [tex]n+1=1[/tex], [tex]n+1=2[/tex] e [tex]n+1=4[/tex]; e, com isso, teríamos [tex]n=0[/tex], [tex]n=1[/tex] e [tex]n=3[/tex]. Mas, pelos dados do problema, [tex]n[/tex] é um número inteiro maior do que [tex]1[/tex]; portanto, [tex]\fcolorbox{black}{#eee0e5}{$n=3$}[/tex].

Solução elaborada pelos Moderadores do Blog.

Solução 2

Se utilizarmos a fórmula que nos garante que a área de um triângulo pode ser obtida multiplicando-se o semiperímetro desse triângulo pelo raio da circunferência nele inscrita, poderíamos obter a expressão [tex]\textcolor{#800000}{(i)}[/tex] da solução anterior de uma outra forma. (Se você não se lembra desse resultado, dê uma olhada na propriedade (5) desta página.)
Vamos então fazer uma segunda solução para este problema e nela vamos também utilizar as duas figuras iniciais da Solução 1.

Observando a figura da direita, vemos um triângulo cujos lados medem [tex] n^2+1, 4n, n^2+1[/tex] e a altura mede [tex]n^2-1[/tex]. A área [tex]S[/tex] desse triângulo pode ser obtida por:
[tex]\qquad \qquad S=\dfrac{\text{base} \times \text{altura}}{2}=\dfrac{4n \times (n^2-1)}{2}[/tex]
[tex]\,\\
\qquad \qquad S=\text{semiperímetro} \times r=\dfrac{n^2+1+4n+n^2+1}{2} \times r.[/tex]
Assim, segue que:

[tex]\qquad \qquad \dfrac{4n \times (n^2-1)}{2}=\dfrac{n^2+1+4n+n^2+1}{2} \times r[/tex]
[tex]\qquad \qquad 4n \times (n^2-1)=\left(n^2+1+4n+n^2+1\right) \times r[/tex]
[tex]\qquad \qquad 4n \times (n^2-1)=\left(2n^2+2+4n\right) \times r[/tex]
[tex]\qquad \qquad 2n \times (n^2-1)=\left(n^2+1+2n\right) \times r[/tex]
[tex]\qquad \qquad 2n \times (n+1)\times (n-1)=\left(n+1\right)^2 \times r[/tex]
[tex]\qquad \qquad 2n \times (n-1)=\left(n+1\right) \times r[/tex]
[tex]\qquad \qquad r=2n\times\dfrac{n-1}{n+1}.\qquad \qquad \textcolor{#800000}{(i)}[/tex]

Daqui para frente, a finalização é idêntica à da solução anterior.

Solução elaborada pelos Moderadores do Blog.