Problema
(Indicado a partir do 1º ano do E. M.)
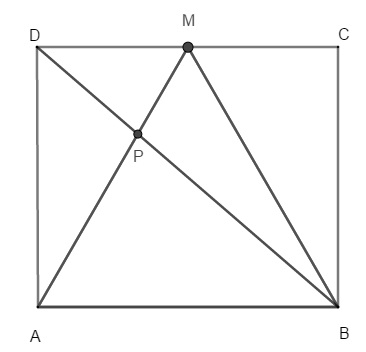
(Coleção Fundamentos de Matemática Elementar– Volume 9) Na figura, [tex]ABCD[/tex] é um retângulo, [tex]M[/tex] é o ponto médio do segmento [tex]\overline{CD}[/tex] e o triângulo [tex]ABM[/tex] é equilátero. Sabendo que a medida de [tex]\overline{AB}[/tex] é [tex]15[/tex], calcule a medida de [tex]\overline{AP}[/tex].

Lembretes
(1) As três medianas de um triângulo interceptam-se em um mesmo ponto (Baricentro) que divide cada mediana em duas partes tais que a parte que contém o vértice é o dobro da outra.
(2) As diagonais de um retângulo intersectam-se mutuamente ao meio.
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X\,[/tex] e [tex]\, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY.[/tex]
Solução 1
Como o triângulo [tex]ABM[/tex] é equilátero temos que [tex]AM=15[/tex]. Agora, considerando o triângulo [tex]ACD[/tex], vamos observar as suas três medianas.
- Como [tex]M[/tex] é o ponto médio do segmento [tex]\overline{CD}[/tex], temos que [tex]\overline{AM}[/tex] é a mediana relativa ao vértice [tex]A[/tex].
- Como [tex]ABCD[/tex] é um retângulo, pelo Lembrete 2 temos que o segmento [tex]\overline{DB}[/tex] contém a mediana que liga o vértice [tex]D[/tex] ao ponto médio do lado [tex]\overline{AC}[/tex].
- Vamos traçar a terceira mediana, que liga o vértice [tex]C[/tex] ao ponto médio do lado [tex]\overline{AD}.[/tex] (Rigorosamente, não há necessidade de se traçar a terceira mediana para obtermos o baricentro de um triângulo: bastam duas medianas. Mas vamos fazê-lo para um melhor entendimento desta solução.)
Vejam a figura abaixo e observem que o ponto [tex]P[/tex] é exatamente o Baricentro do triângulo [tex]ACD[/tex].
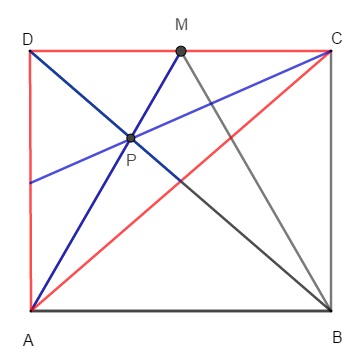
Pelo Lembrete 1, se [tex]PM=x[/tex], temos que [tex]AP=2x[/tex]. Assim, [tex]2x+x=15[/tex] e, com isso, [tex]x=5[/tex].
Portanto, [tex]AP=2x=2\cdot 5=10[/tex], ou seja, a medida do segmento [tex]\overline{AP}[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$10$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Faremos uma segunda solução utilizando semelhança de triângulos. Para isso, observe os ângulos destacados na próxima figura.
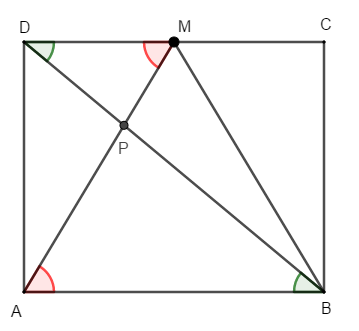
Vemos que os ângulos de mesma cor são congruentes por serem ângulos alternos internos.
(Precisa relembrar esse conceito? Dê uma passadinha nesta Sala.)
Com isso, pelo caso de semelhança de triângulos ângulo-ângulo, temos que os triângulos [tex]PMD[/tex] e [tex]PAB[/tex] são semelhantes. Assim:
[tex]\qquad \boxed{\dfrac{DM}{AB}=\dfrac{PM}{AP}}. \qquad \qquad \textcolor{#800000}{(i)}[/tex]
(Para saber mais sobre semelhança de triângulos, visite esta Sala para Leitura .)
Como [tex]DC=AB=15[/tex] e [tex]M[/tex] é o ponto médio de [tex]\overline{DC}[/tex], temos que [tex]DM=\dfrac{15}{2}[/tex]. Então, segue de [tex]\textcolor{#800000}{(i)}[/tex] que:
[tex]\qquad \dfrac{\frac{15}{2}}{15}=\dfrac{PM}{AP}\\
\qquad \dfrac{15}{2}\times AP=15 \times PM \\
\qquad AP=2\times PM. \qquad \qquad \textcolor{#800000}{(ii)} [/tex]
Por outro lado, temos que [tex]AM=AP+PM[/tex]; assim,
[tex]\qquad AM=2PM+PM=3PM.[/tex]
Sendo [tex]AM=15[/tex], então [tex]15=3PM[/tex] e, portanto, [tex]PM=5[/tex].
Logo, por [tex] \textcolor{#800000}{(ii)} [/tex], [tex]\fcolorbox{black}{#eee0e5}{$AP=10$}[/tex] .
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
