Problema
(Indicado a partir do 9º ano do E. F.)
Em um círculo de área [tex]9 \;cm^2[/tex] , traçam-se duas cordas [tex]AB[/tex] e [tex]AC[/tex], tais que:
I) O arco [tex]AB[/tex] mede [tex]70^\circ[/tex] ([tex]\stackrel{\frown}{AB}=70^\circ[/tex]);
II) O ângulo [tex]BAC[/tex] mede [tex]20^\circ[/tex] ([tex]B\widehat A C=20^\circ[/tex]).
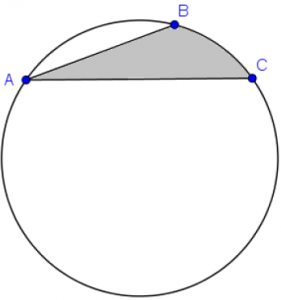
Calcule a medida da área cinza da figura.

AJUDA
(1) Se duas retas paralelas são intersectadas por uma transversal, então os pares de ângulos alternos internos que essa transversal define são congruentes. (Precisa relembrar estes conceitos? Dê uma passadinha nesta Sala.)
(2) Se você não se lembra ou não sabe o que é um ângulo central, o que é um ângulo inscrito e como obter suas medidas, clique AQUI.
(3) Se você não se lembra ou não sabe o que é um setor circular e o que é um segmento circular, clique AQUI.
Notações:
– Denotaremos o comprimento do arco definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\stackrel{\frown} {XY}. [/tex]
– Denotaremos a medida do ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]X\widehat{V}Y. [/tex]
Solução
Inicialmente, perceba que a área desejada é a soma da área do triângulo [tex]ABC[/tex] com a área do segmento circular delimitado pela corda [tex]BC[/tex] e pelo arco [tex]BC[/tex].
Agora, vamos construir a reta [tex]BC[/tex] e também a reta [tex]AD[/tex], paralela à reta [tex]BC[/tex] e que passa por [tex]A[/tex].
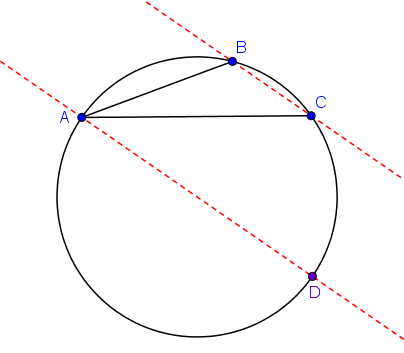
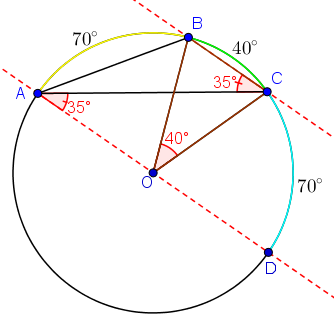
Como [tex]\stackrel{\frown}{AB}=70^\circ[/tex], pela definição de ângulo inscrito, concluímos que [tex]B\widehat C A=35^\circ[/tex]. Com isso, temos que [tex]C\widehat A D=35^\circ[/tex], já que as retas são paralelas e os ângulos representam um par de ângulos alternos internos.
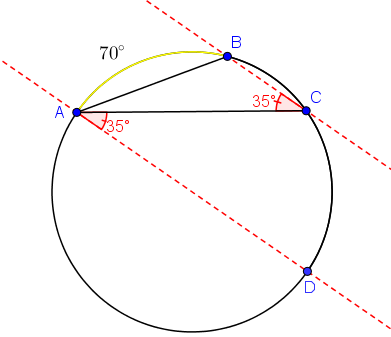
Do exposto acima e utilizando novamente a definição de ângulo inscrito, obtemos que [tex]\stackrel{\frown}{CD}=70^\circ[/tex]. Do enunciado, temos que [tex]B\hat A C=20^\circ[/tex], logo [tex]\stackrel{\frown}{BC}=40^\circ[/tex]. Dessa forma, [tex]\stackrel{\frown}{AD}=180^\circ[/tex] e, portanto, a reta [tex]AD[/tex] passa pelo centro [tex]O[/tex] do círculo.
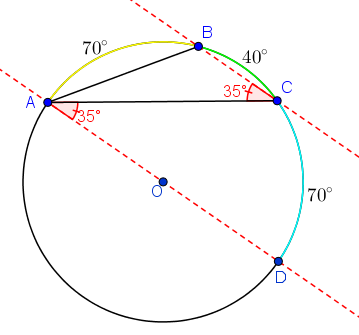
Construindo o triângulo [tex]OBC[/tex] e utilizando a definição de ângulo central, temos que [tex]B\hat O C=40^\circ[/tex].
Agora, note que os triângulos [tex]ABC[/tex] e [tex]OBC[/tex] possuem a mesma área, pois ambos têm o segmento [tex]BC[/tex] como base e a distância entre as retas paralelas como altura. Com isso, a área desejada é a soma da área do triângulo [tex]OBC[/tex] com o segmento circular delimitado pelo arco [tex]BC[/tex] e a corda [tex]BC[/tex], ou seja, a área desejada é a área do setor circular [tex]OBC[/tex].
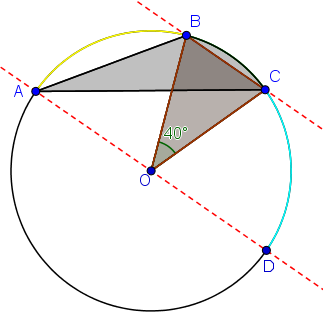
Por fim, a área do setor circular é dada por
[tex]\qquad \qquad A=\dfrac{40^\circ}{360^\circ} \cdot 9 = 1 \;cm^2[/tex]
e, portanto, a medida da área cinza da figura apresentada no problema é [tex]\fcolorbox{black}{#eee0e5}{$ 1 \;cm^2$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
