✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Médio)
Uma escola encomendou para um artesão lembranças natalinas na forma de um lápis, para distribuir aos seus professores. Esses lápis foram confeccionados a partir de cones e cilindros circulares retos, como mostra a figura abaixo.
Qual a área lateral, a área total e o volume de cada um desses lápis?
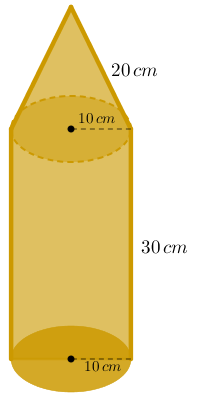
(Problema adaptado do livro Matemática, volume único– Gelson Iezzi & outros)

Lembretes
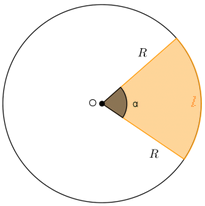
✐ Área de um setor circular de raio [tex]R[/tex] e comprimento de arco [tex]l[/tex]:
[tex]\qquad \qquad\boxed{A_{setor}=\dfrac{l\times R}{2}}[/tex]
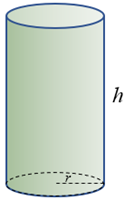
(Para aprender um pouco mais sobre setor circular, clique AQUI.)
✐ Volume de um cilindro circular reto cujo comprimento da altura é [tex]h[/tex] e o comprimento do raio da base é [tex]r[/tex]:
[tex]\qquad \qquad \boxed{Volume=\pi \, r^2 h} \, \, .[/tex]
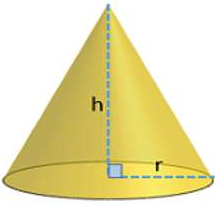
✐ Volume de um cone circular reto cujo comprimento da altura é [tex]h[/tex] e o comprimento do raio da base é [tex]r[/tex]:
[tex]\qquad \qquad \boxed{Volume= \dfrac{\pi r^2h}{3}}. [/tex]
Solução
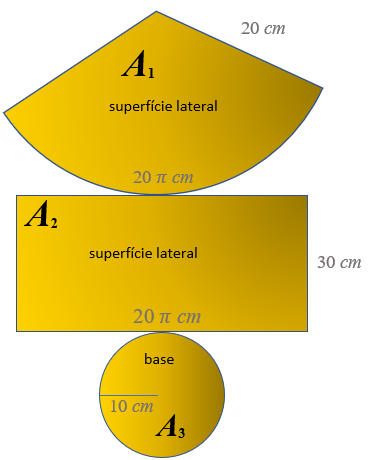
(a) A figura ao lado mostra que a superfície lateral do lápis é a superfície lateral de um cilindro circular reto e a superfície lateral de um cone circular reto:
- a superfície lateral do cilindro é um retângulo de dimensões [tex]20\,\pi[/tex] (comprimento da circunferência da base) e [tex]30[/tex];
- a superfície lateral do cone é um setor circular de raio [tex]20[/tex] (geratriz do cone) e cujo comprimento de arco é [tex]20 \, \pi[/tex] (comprimento da circunferência da base).
Assim, a área lateral [tex]A_{lat}[/tex] é a soma das áreas [tex]A_1[/tex] e [tex]A_2[/tex] indicadas na figura.
Vamos calculá-las.
- Área do retângulo:
- Área do setor circular:
[tex]\qquad A_2=20\,\pi\times 30=600\,\pi\,\text{cm}^2 \, .[/tex]
Utilizando a primeira fórmula do Lembrete, temos que:
[tex]\qquad A_{1}=\dfrac{20\,\pi\times 20}{2}=200\,\pi\,\text{cm}^2 \, .[/tex]
Assim,
[tex]\qquad A_{lat}=A_1+A_2=200\,\pi+600\,\pi=800\,\pi \, [/tex],
ou seja, a área lateral do lápis é [tex] \, \fcolorbox{black}{#eee0e5}{$800\,\pi\,\text{cm}^2$} \, .[/tex]
(b) A figura lateral acima nos indica que a área total do lápis, [tex]A_t[/tex], é a soma [tex]A_1+A_2+A_3[/tex], sendo [tex]A_3[/tex] a área de um círculo de raio [tex]10\,\text{cm}[/tex].
Já temos os valores [tex]A_1[/tex] e [tex]A_2[/tex]; vamos calcular [tex]A_3[/tex]:
[tex]\qquad A_3=10^2\times\pi=100\,\pi[/tex].
Portanto:
[tex]\qquad A_t=A_1+A_2+A_3=200\,\pi+600\,\pi+100\,\pi=900\,\pi[/tex]
e, com isso, a área total do lápis é [tex] \, \fcolorbox{black}{#eee0e5}{$900\,\pi\,\text{cm}^2$} \, .[/tex]
(c) O volume [tex]V[/tex] do lápis é a soma do volume [tex]V_{cone}[/tex] de um cone circular reto e do volume [tex]V_{cil}[/tex] de um cilindro circular reto.
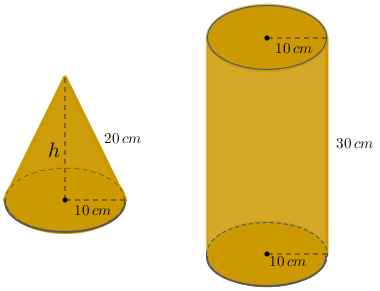
Façamos os cálculos:
- Volume de um cone circular reto com raio da base [tex]10\,\text{cm}[/tex] e altura [tex]h[/tex], sendo [tex]h[/tex] o segundo cateto de um triângulo retângulo de hipotenusa com comprimento [tex]20\,\text{cm}[/tex] e um cateto com comprimento [tex]10\,\text{cm}[/tex] (terceira fórmula do Lembrete):
- Volume de um cilindro circular reto com raio da base [tex]10\,\text{cm}[/tex] e altura [tex]30\,\text{cm}[/tex] (segunda fórmula do Lembrete):
[tex]\qquad V_{cone}=\dfrac{\pi \cdot 10^2 \cdot h}{3} \, .[/tex]
Aqui precisaremos do valor de [tex]h[/tex]. Para isso, utilizaremos o Teorema de Pitágoras:
[tex]\qquad h^2+10^2=20^2\\
\qquad h^2=400-100\\
\qquad h^2=300\\
\qquad h=10\sqrt{3}.\\[/tex]
Finalizando o cálculo do volume, obtemos:
[tex]\qquad V_{cone}=\dfrac{\pi \cdot 10^2 \cdot 10\sqrt{3}}{3}=\dfrac{1000\sqrt{3} \, \pi }{3} \, \text{cm}^3 \, .[/tex]
[tex]\qquad V_{cil}=\pi\cdot 10^2 \cdot 30=3000 \, \pi \, \text{cm}^3 \, .[/tex]
Portanto, segue que:
[tex]\qquad \qquad V=V_{cone}+V_{cil}\\
\qquad \qquad V=\dfrac{1000\sqrt{3} \, \pi }{3}+3000 \, \pi\\
\qquad \qquad V=\dfrac{1000\sqrt{3} \, \pi +9000 \, \pi}{3}\\
\qquad \qquad V=\dfrac{1000\pi}{3}\cdot\left(\sqrt{3}+9\right).\\
[/tex]
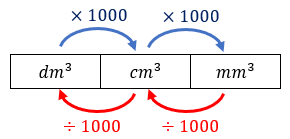
Temos, então, que o volume do lápis é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{1000\pi}{3}\cdot\left(\sqrt{3}+9\right)\,\text{cm}^3$} \, [/tex], ou aproximadamente, [tex] \, \fcolorbox{black}{#eee0e5}{$11 \, 232,88 \, \text{cm}^3$} \, [/tex], ou ainda,[tex] \, \fcolorbox{black}{#eee0e5}{$11,2 \, dm^3$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
