.Desafio: O problema dos 1000 dinares

Problema
(Indicado a partir do 8º ano do E. F.)

---

O problema dos 1000 dinares
(adaptado do livro Novas Lendas Orientais, de Malba Tahan)

Determinar como mil moedas de um dinar foram distribuídas em dez baús do mesmo tamanho, numerados e fechados, de maneira que:
a) a numeração dos baús, de 1 até 10, foi feita em ordem estritamente crescente, relativa ao conteúdo de moedas que cada um encerra;
b) seja possível fazer qualquer pagamento, de 1 até 1000 dinares, sem precisar abrir os baús.

Solução

---

Distribuiremos em cada baú, do primeiro ao décimo, respectivamente as seguintes quantidades de moedas:
[tex]\qquad \qquad 1=2^0;\, 2=2^1;\, 4=2^2;\, 8=2^3;\, 16=2^4; \, 32=2^5; \\
\qquad \qquad 64=2^6;\, 128=2^7;\, 256=2^8 \text{ e } 489 .[/tex]
Perceba que, com essa distribuição associamos uma potência de [tex]2[/tex] a cada baú, com exceção do décimo e último baú.
Agora, dispondo os dez baús da seguinte forma:

conseguiremos pagar qualquer dívida até mil dinares.
Observe…

(1) Dívidas até 511 dinares:
(i) Primeiro transformamos o número que representa a dívida da base decimal para a base binária, que é a “base dos baús de um a nove”.
Por exemplo, o número que na base decimal escrevemos como [tex]\, 500[/tex] é escrito na base binária como [tex]\, 111110100[/tex], pois:
[tex]\quad\, 1\cdot2^8+1\cdot2^7+1\cdot2^6+1\cdot2^5+1\cdot2^4+0\cdot2^3+1\cdot2^2+0\cdot2^1+0\cdot2^0=[/tex]
[tex]\qquad \, =256+128+64+32+16+0+4+0+1=500.\quad[/tex](*)
(ii) Usamos, então, os algarismos [tex]0[/tex] e [tex]1[/tex] da representação binária para indicar se utilizamos ou não os respectivos baús para pagar uma dívida:
algarismo [tex]0[/tex]: não precisamos das moedas do baú, logo o baú não será utilizado no pagamento da dívida;
algarismo [tex]1[/tex]: precisamos das moedas do baú, logo o baú será utilizado no pagamento da dívida.
O pagamento da nossa dívida de [tex]500[/tex] dinares ficaria assim:

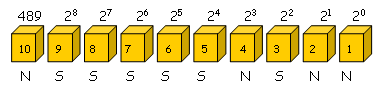
ou seja, utilizaríamos os baús de números [tex]3,\, 5, \, 6, \, 7, \, 8\, [/tex] e [tex]\, 9.[/tex]
Como podemos representar na base binária qualquer número natural que seja representado na base decimal de [tex]1[/tex] a [tex]511[/tex] utilizando nove algarismos [tex]0[/tex] e [tex]1[/tex], utilizamos os baús que contenham o número de moedas correspondentes e pagamos dívidas de [tex]1[/tex] a [tex]511[/tex] dinares.
(Represente [tex]511[/tex] na base binária e verifique a veracidade dessa afirmação)
 
(2) Dívidas de 512 a 1000 dinares:
Para pagarmos uma dívida de [tex]d[/tex] dinares, com [tex]511 \lt d \le 1000[/tex], escolhemos inicialmente o baú número [tex]10[/tex] para obtermos [tex]489[/tex] dinares. Como o restante da dívida será [tex]r= d-489[/tex] dinares, então [tex]r[/tex] será tal que [tex]23\le r \le 511[/tex]; assim, pelo item (1) conseguimos esse valor utilizando os baús numerados de um a nove.
De outra forma, qualquer número maior que [tex]511[/tex] e menor ou igual [tex]1000[/tex], poder ser escrito como [tex]489+n[/tex], com [tex]n[/tex] menor ou igual a [tex]511[/tex], e dívidas de até [tex]511[/tex] dinares pagamos de acordo com o item (1).

(*) Para entender essa forma de representar o 500, assista ao Vídeo 1 do PIC.

---

Solução enviada pelo Clube Os Pitagóricos e complementada pelos Moderadores do Blog.