Problema
(Indicado a partir do 9º ano do E. F.)
A figura a seguir representa a bússola do painel de um avião de carga e com ela o piloto determina as suas rotas.
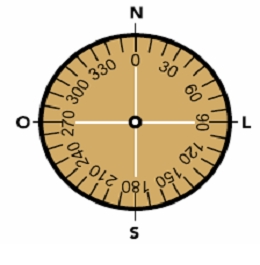
Diariamente, esse avião decola de uma certa cidade A e alcança a cidade B após duas horas de voo na rota [tex]28^\circ[/tex].
Certo dia, porém, em um voo noturno, ao decolar, o piloto automático foi acionado; mas, por engano, foi digitada a rota [tex]280^\circ[/tex], ao invés de [tex]28^\circ[/tex]. Duas horas após a decolagem, o piloto percebeu que não estava na cidade B e só então notou o equívoco.
Supondo que o avião tenha combustível suficiente, qual o ângulo da nova rota que ele deverá seguir para atingir a cidade B?
Extraído do Simulado para o ENEM 2012 da escola Ari de Sá.
AJUDA
Pelas discussões percebemos que alguns Clubes tiveram dificuldade no entendimento do enunciado do problema.
Note que, como a duração do voo foi a mesma, consideramos que as cidades B e E têm a mesma distância da cidade A. Assim, fizemos estas figuras para tentar ajudar.
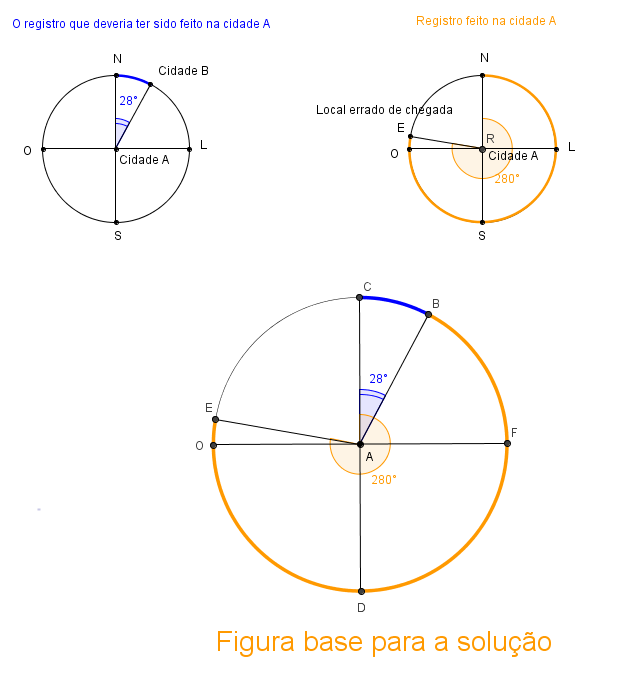
Observamos que consideraremos as medidas dos ângulos marcadas no sentido horário, de acordo com a leitura da bússola a ser utilizada.

Lembretes
(1) Se duas retas paralelas são intersectadas por uma transversal, então os pares de ângulos alternos internos que essa transversal define são congruentes. (Precisa relembrar esses conceitos? Dê uma passadinha nesta Sala.)
(2) A soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ\,.[/tex]
(3) Todo triângulo isósceles possui os ângulos da base com a mesma medida.
Solução
Inicialmente, observe que a rota correta corresponde ao ângulo [tex]C \hat AB[/tex] cuja medida é [tex]28^\circ[/tex], mas foi digitada a medida [tex]280^\circ[/tex], correspondente ao ângulo [tex]C\hat AE[/tex].
A partir da figura base, vamos determinar as medidas de dois ângulos que poderão ajudar na solução do problema.
- Como a medida de [tex]C\hat AO[/tex] é [tex]270^\circ[/tex], então a medida de [tex]O\hat AE~[/tex] é [tex]~\boxed{280^\circ-270^\circ=\textcolor{#800000}{10^\circ}}.[/tex]
- Como a medida de [tex]O\hat AE~[/tex] é [tex]10^\circ[/tex] e a medida de [tex]O\hat AC~[/tex] é [tex]90^\circ[/tex], então a medida de [tex]E\hat AC~[/tex] é [tex]~\boxed{90^\circ-10^\circ=\textcolor{#006400}{80^\circ}}.[/tex]
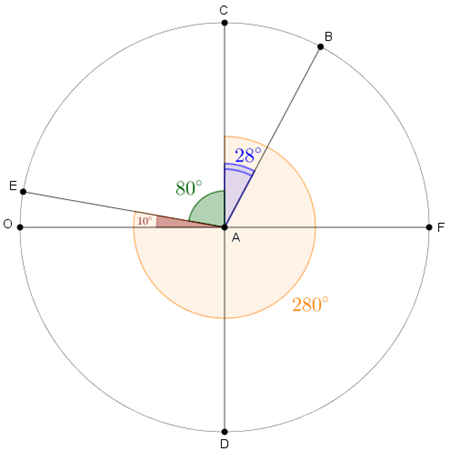
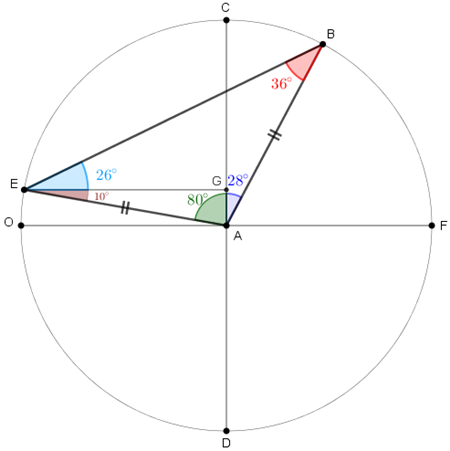
Agora, considere o segmento [tex]\overline{EG}[/tex] tal que [tex]\overline{EG}//\overline{OA}[/tex], conforme ilustra a figura a seguir. Daí, [tex]G\hat EA[/tex] é um ângulo de [tex]10^\circ[/tex] e [tex]E\hat AG[/tex] mede [tex]80^\circ[/tex].
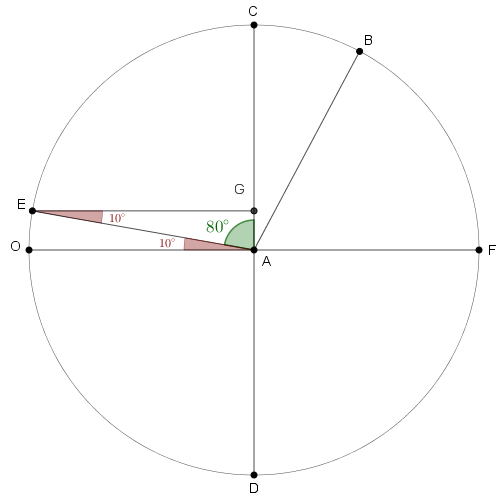
Observe a figura a seguir. Como o triângulo [tex]\triangle BAE[/tex] é isósceles ([tex]\overline{AB}[/tex] e [tex]\overline{AE}[/tex] são raios da circunferência, já que consideramos que as cidades B e E têm a mesma distância da cidade A) e a medida do ângulo [tex]E \hat AB[/tex] é [tex]~\boxed{80^\circ+28^\circ=108^\circ}[/tex], então os ângulos [tex]A \hat BE[/tex] e [tex]B\hat EA[/tex] são côngruos com medida [tex]~\boxed{\dfrac{180^\circ-108^\circ}{2}=\textcolor{red}{36^\circ}}[/tex], donde concluímos que a medida do ângulo [tex]G\hat EB[/tex] é [tex]~\boxed{36^\circ-10^\circ=\textcolor{#0099FF}{26^\circ}}[/tex].
Para traçar a nova rota, consideremos o segmento [tex]\overline{EH}[/tex] perpendicular a [tex]\overline{EG}[/tex], uma vez que essa rota vai ser definida a partir do ponto [tex]E[/tex].
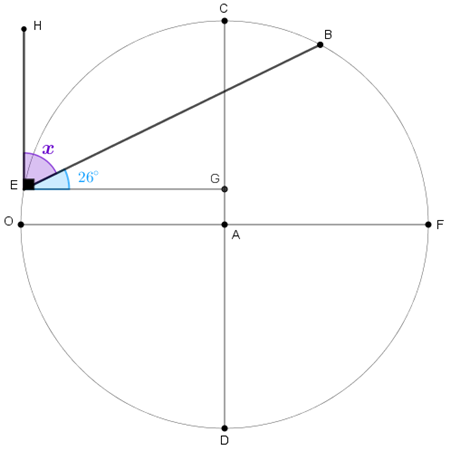
Logo, o ângulo [tex]H\hat EB [/tex] da nova rota deve ter medida [tex]\fcolorbox{black}{#f6eeff}{$ {\textcolor{#6600CC}{x=\textcolor{black}{90^\circ}-\textcolor{#0099FF}{26^\circ}=64^\circ}}$}~.[/tex]
Solução elaborada pelos Moderadores do Blog.
Participaram da discussão do problema os seguintes Clubes: Erudio; Math Error.
